|
| [44] Hajba Károly | 2004-09-07 13:12:45 |
 Üdv Mindekinek!
Általános iskola 5. osztályos szintű, korábbi évek matek versenyfeladatsorait keresem lányom részére felkészülés, gyakorlás céljából. Kinek rendelkezésére áll ilyen értestsen. Előre is köszönöm.
Hajba Károly
|
|
|
|
|
|
| [39] Csimby | 2004-05-25 22:43:57 |
 Hoppá, most látom az volt a kérdés melyik a legkisebb többszörös. Tehát hülyeséget írtam ...
|
|
| [38] Csimby | 2004-05-25 22:39:01 |
 Vegyük a következő sorozatot: 1997, 2*1997, 3*1997, 4*1997,...,10000*1997 Ez 10000 tag, mivel 1997 prím, ebben a sorozatot modulo 10000 véve minden maradék pontosan egyszer szerepel, ezt most nem bizonyítom, de nem nehéz (teljes maradék rendszert alkotnak, vagy micsodát). Tehát szerepel modulo 1998-is, egy szám pedig 10000-rel osztva akkor ad 1998 maradékot, ha arra végződik (hiszen a...z0000 osztható 10000-rel)! Ez csak a megoldás létezését bizonyítja, de asszem csak ez volt a kérdés.
|
| Előzmény: [37] lorantfy, 2004-05-25 17:54:35 |
|
|
| [36] plx | 2004-05-25 17:42:12 |
 Gondoljunk egy B középpontú 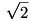 r sugarú gömbre. (A körfűrész persze nem vágná ki, mert a körfűrészlap megakadályozza az elfordulásban, "körfűrészív" lenne jó.) r sugarú gömbre. (A körfűrész persze nem vágná ki, mert a körfűrészlap megakadályozza az elfordulásban, "körfűrészív" lenne jó.)
|
| Előzmény: [12] lorantfy, 2003-12-11 13:08:19 |
|
|
| [34] plx | 2004-05-25 15:10:49 |
 Indirekt. Vegyük a konvex burkot. Ennek csak háromszög lapja lehet, különben egyszerű. Mindkét típusú háromszöglap esetén könnyen adódik a megoldás, ha a lap síkjára eső vetületeket figyeljük. Tehát nincs ilyen térbeli ötszög.
|
| Előzmény: [10] lorantfy, 2003-12-10 22:03:47 |
|
| [33] lorantfy | 2004-05-19 23:48:24 |
 9. feladat: Az 1997-nek melyik az a legkisebb többszöröse, amelyik 1998-ra végződik?
Makkosházi Matematika Verseny 2004 (7. osztály!)
|
|
| [32] lorantfy | 2004-04-29 21:35:24 |
 Kedves Fórumosok!
Arra gondoltam, hogy majd írtok be megoldások a lenti Arany Dániel feladatokra.
Kedvcsinálónak az I./3. megoldása:
2004182 < 2048182 = 211.182 = 22002 < 22004
8. feladat: Hány év múlva lesz először igaz, ha k az évszám és m,n egész számok, hogy
kn =mk
Pl. 65536-ban:
655364096 = 265536
|
| Előzmény: [31] lorantfy, 2004-04-24 21:27:23 |
|
| [31] lorantfy | 2004-04-24 21:27:23 |
 Kedves Fórumosok!
Április 22-én volt az Arany Dániel verseny döntője. Egy kategória kivételével mindegyikben volt 2004-el kapcsolatos feladat. Ezeket tenném itt közzé, ha nem ütközik jogi akadályokba:
Kezdők I./3. Melyik nagyobb 22004 vagy 2004182?
Kezdők II./2. Mely x,y, és z egész számokra igaz a következő egyenlőség?
x2+y2+z2=22004
Kezdők III./1. Melyik nagyobb a következő számok közül: 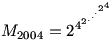 vagy vagy 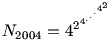 ? Mindkét emeletes hatványban 2004 db szám szerepel, váltakozva kettesek és négyesek. ? Mindkét emeletes hatványban 2004 db szám szerepel, váltakozva kettesek és négyesek.
Kezdők III./2. Tekintsük a következő számot: 444...4449, ahol az utolsó számjegy kivételével minden más jegy négyes, számjegyeinek száma pedig 2004-nek többszöröse. Bizonyítsuk be, hogy ez a szám nem egy prímszám négyzete!
Haladók I-II./3. Legfeljebb hány egész szám adható meg úgy, hogy semelyik kettő összege, semelyik kettő különbsége és semelyik kettő szorzata se legyen osztható 2004-gyel?
|
|
|
| [29] Rácz Béla | 2004-01-14 19:49:19 |
 Kedves fórumos diákok!
Igazából nem tudom, hogy ezt melyik fórumbe írjam, de - bár van róla szó a friss KöMaL-ben - szeretném én is mindenkinek felhívni a figyelmét a
KAVICS-pályázatra.
A részleteket a Fazekas-honlapon találhatjátok meg.
|
|
| [28] Zormac | 2004-01-14 16:17:33 |
 Bátortalan első hozzászólóként én is bedobom a kedvenc olimpiai példámat (igaz, ez nem geometria):
Hány olyan p-elemű részhalmaza van az {1,2,...,2p} halmaznak, amelynek elemeinek összege osztható p-vel? (p páratlan prím)
Az olimpiai példák egyébként remekül böngészhetők például ezen a címen: http://imo.math.ca/
-- z.
|
|
| [27] Sirpi | 2004-01-14 13:22:18 |
 Szia Nadorp!
Gratula a megoldáshoz! Hajszálpontosan így csináltam én is, csak az enyémet lassabb lett volna beírni, mert a,b,c helyett  , , , , -t használtam :-) -t használtam :-)
S
|
| Előzmény: [26] nadorp, 2004-01-14 11:40:55 |
|
| [26] nadorp | 2004-01-14 11:40:55 |
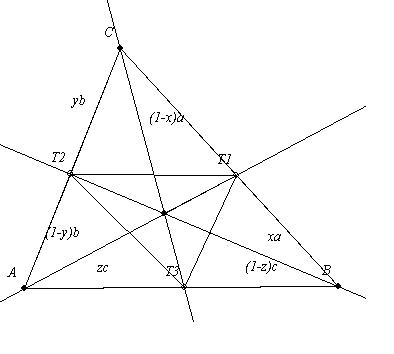
 Közlök a 6.b feladatra egy számolásos (nem annyira geometriai) megoldást.
Tegyük fel, hogy a BT1=xa,CT2=yb és AT3=zc (0<x,y,z<1, lásd az ábrát).Ekkor nyilván
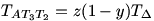
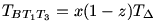
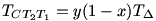 , ezért a bizonyítandó egyenlőtlenség: , ezért a bizonyítandó egyenlőtlenség:
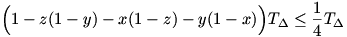
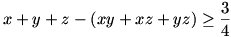
A Ceva tétel ( remélem tényleg az !!) szerint viszont
xa.yb.zc=(1-x)a.(1-y)b.(1-z)c, ahonnan következik,hogy
x+y+z-(xy+xz+yz)=1-2xyz, ezért elegendő bizonyítani, hogy
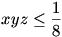 , ami következik az alábbi egyenlőtlenségekből: , ami következik az alábbi egyenlőtlenségekből:
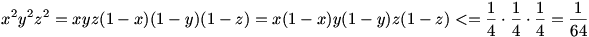
|
 |
|
|
| [24] lorantfy | 2004-01-13 23:40:56 |
 Kedves Géza, Sirpi és Fórumosok !
Nagy élvezettel olvastam Géza megoldását és persze az ábrák is nagyon tetszettek. Örülök Sirpi általánosításának. Egy egyszerű megoldás a 6. feladatra: Tekintsük a talpponti  csúcsai közül az ABC csúcsai közül az ABC legnagyobb szögével szemben lévőt és húzzunk párhuzamosokat rajta keresztül a másik két oldallal. A párhuzamosok az oldalakat D és E pontban metszik. legnagyobb szögével szemben lévőt és húzzunk párhuzamosokat rajta keresztül a másik két oldallal. A párhuzamosok az oldalakat D és E pontban metszik.
T1T3B =T2T3A =T2T3A = = és mivel ez a legnagyobb szög ezért T1 és T2 a CDT3E paralelogramma megfelelő oldalaira esnek. és mivel ez a legnagyobb szög ezért T1 és T2 a CDT3E paralelogramma megfelelő oldalaira esnek.
Először belátjuk, hogy 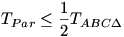 majd, hogy majd, hogy 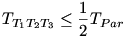 amiből amiből 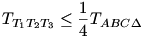
1. Válasszuk AT3 és T3B közül a kisebb (egyenlő) szakaszt és húzzunk D pontból párhuzamost AB-vel. Látható, hogy 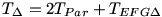 és és 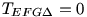 csak akor lehetséges, ha T3 AB oldal felezőpontja. csak akor lehetséges, ha T3 AB oldal felezőpontja.
2. CDT3E paralelogrammában T1 pontból húzzunk párhuzamost CD-vel, T2-ből pedig CE-vel.(fenti ábra) Látható, hogy T1T2T3G négyszög területe a paralelogramma területének fele. T1T3G területe csak akkor 0, ha T1=E vagy T2=D, ilyenkor egyenlőség van, különben területe csak akkor 0, ha T1=E vagy T2=D, ilyenkor egyenlőség van, különben 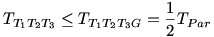 Talán Sirpi 6.b általánosítására is átdolgozható, de még nem volt időm rá. Talán Sirpi 6.b általánosítására is átdolgozható, de még nem volt időm rá.
|
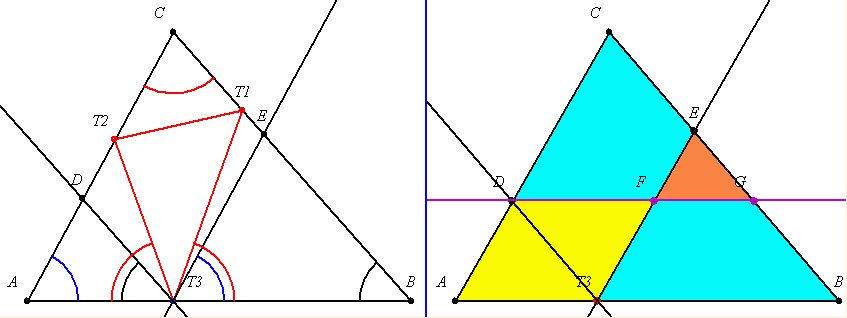 |
| Előzmény: [22] Kós Géza, 2004-01-13 11:28:20 |
|
| [23] Sirpi | 2004-01-13 13:19:40 |
 Sziasztok!
Géza, frappáns a megoldásod, de elolvasása közben felvetődött bennem a gondolat, hogy nyilván a magasságvonalak talppontjain kívül más belső pontokhoz tartozó talppontokra is igaz, hogy legfeljebb T/4 területú háromszöget határoznak meg. Gyors számolás után be is láttam, hogy ez minden belső pontra igaz. Úgyhogy ez lehet akár egy, mondjuk a
6b feladat: Az ABC háromszög belső pontja P. Az AP egyenes a BC oldalt a D pontban metszi, és hasonlóan adódnak a másik két csúcsból az E és F talppontok. Biz. be: 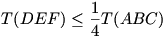
|
| Előzmény: [22] Kós Géza, 2004-01-13 11:28:20 |
|
| [22] Kós Géza | 2004-01-13 11:28:20 |
 Az egyenlőtlenséget számolás nélkül is be lehet bizonyítani, igaz, így nehezebb is....
Először is egy lemma. Legyen PQR egy tetszőleges háromszög, a körülírt körén a PQ, QR, RP ívek felezőpontjai FR, FP, illetve FQ. Ekkor a PFRQFPRFQ hatszög területe legalább kétszerese a PQR háromszög területének.
Bizonyítás: Először azt az esetet vizsgáljuk, amikor PQR hegyesszögű. A magasságpontja legyen M, ami a háromszög belsejében van. A magasságpont tükörképei az oldalegyenesekre legyenek TP, TQ és TR, ezek rajta vannak a körülírt körön (1. ábra). A tükrözés miatt a PTRQ háromszög területe megegyezik a PQM háromszög területével. A PQ körív legtávolabbi pontja a PQ egyenestől FR, ezért t(PFRQ ) ) t(PTRQ t(PTRQ )=t(PQM )=t(PQM ). (Egyenlőség akkor van, ha a TR és FR pontok egybeesnek, azaz PR=QR.) Másképpen fogalmazva, a PFRQM négyszög területe legalább kétszerese a PQM háromszögének. ). (Egyenlőség akkor van, ha a TR és FR pontok egybeesnek, azaz PR=QR.) Másképpen fogalmazva, a PFRQM négyszög területe legalább kétszerese a PQM háromszögének.
Hasonlóan kapjuk, hogy a QFPRM és RFQPM négyszögek területe legalább kétszerese a QRM és RPM háromszögek területének, összesen tehát a PFRQFPRFQ hatszög területe legalább kétszerese a PQR háromszög területének. Egyenlőség akkor van, ha a PQR háromszög szabályos.
Ha a PQR háromszög derék- vagy tompaszögű, például a P-nél levő szöge legalább derékszög, akkor a QFPR háromszög területe egymaga legalább akkora, mint a PQR háromszög területe, és ehhez még hozzájön a PFRQ és az RFQP háromszögek területe (2. ábra).
Teintsük most az ABC háromszög Feuerbach-körét (3. ábra). Ez többek között átmegy a magasságvonalak talppontjain és az AM, BM. CM szakaszok felezőpontjain. Az FA, FB, FC felezőpontok felezik a B1C1, C1A1, A1B1 köríveket, mert a magasságvonalak a talpponti háromszög szögfelezői. Az MB1A, MAC1, ..., MCB1 háromszögek területének az A1FCB1FAC1FB hatszög éppen a felét tartalmazza, ezért, a lemmát is alkalmazva, t(ABC)=2t(A1FCB1FAC1FB) 4t(A1B1C1). 4t(A1B1C1).
|
 |
| Előzmény: [17] lorantfy, 2004-01-11 11:21:59 |
|
| [21] tmbjg | 2004-01-12 17:37:53 |
 Köszönöm, időközben már rájöttem, hogy valószínűleg mire gondolt a feladat írója. Elnézést kérek a kérdésért, gondoltam, hogy ez tabu téma, de tegnap már annyira felidegesített a feladat, hogy nem tudtam jobbat kitalálni. Ma hideg fejjel könnyebb volt. Még egyszer köszönöm. Tisztelettel: Tóth Miklós, Batsányi János Gimnázium
|
|
