| [1624] bily71 | 2012-12-27 23:35:55 |
 Az élek második képe körív hiszen, ha O1-ből végigpásztázunk egy élet, akkor egy síkrészt kapunk, mely metszi a G1 gömböt, a metszet ekkor természetesen körív, így P egy élének első képe G1 egy főkörén van. Ha invertáljuk ezt a kört, akkor megint kört kapunk, vagyis egy él második képe az S síkon fekvő körön van. Mindezeket figyelembe vettem, de egyszerű ábrát akartam készíteni, mert valójában ennek nincs jelentősége. Az E''G' ívből mindegy mi lesz, mert P átforgatásakor az újonnan S-re érkező csúcsok nem lehetnek benne a vetület megfelelő összehúzásokkal már módosított tartományában a következő okok miatt.
Az összehúzást L-1-gyel kezdjük, majd átbillegtetve P-t L1 élein összehúzzuk a megnyúlt szomszédjait is. Utoljára az (ii) szerint kiválasztott L2-t húzzuk össze. Az L1 lap és szomszédai egy síkidomot határoznak meg S-n, melynek körvonala és L1 szomszédainak közös élei mentén, kivéve L2 azon éleit, miket F metsz, az S át van vágva. Miután L1-et a szomszédaival összehúztuk, a kapott síkidom körvonala eltávolodik a régi körvonaltól, mégpedig az összehúzott lapok irányába, így az összehúzott lapok nem metszetnek bele a nem összehúzott lapokba. L-1 szomszédai az összehúzás után nem metszethetnek bele L1-be, sem egymásba, hiszen L1-t szomszédaival együtt kiterítve a síkba a szomszédok közös élei nemhogy fedik egymást, hanem eltávolodnak egymástól. Ez azért van, mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o.
Mikor L2-t és szomszédait összehúzzuk, az L1 és L2 szomszédai által alkotott síkidom új körvonala eltávolodik a régitől, mint az előbb, tehát ez a síkidom sem metsz bele a nem összehúzott lapokba, vagyis nem keletkezik átfedés. L2 még nem összehúzott szomszédait összehúzva (itt is billegtetünk L3 a végére hagyva) az L2 újonnan összehúzott szomszédai nem metszetnek bele L2-be, sem egymásba ugyanazon okokból kifolyólag, mint amit leírtunk már L1 és szomszédai esetében. L2 újonnan összehúzott szomszédai nem metszethetnek bele az előbb összehúzott lapokba sem, hiszen akkor belemetszenének L2 már előzőleg összehúzott szomszédaiba is, ami nem lehet megint csak az előbbiekben már említett okokból. Átfedés tehát itt sem keletkezett.
Az előbbi gondolatmenetet alkalmazhatjuk L3-ra, L4-re és így tovább...
A lényeg még egyszer: Lk újonnan összehúzott szomszédai nem metszethetnek bele az előzőekben összehúzott lapok által alkotott síkidomba, mert akkor belemetszenének Lk már előzőleg összehúzott szomszédaiba is, ami nem lehet, mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o.
|
| Előzmény: [1623] HoA, 2012-12-27 15:04:35 |
|
| [1623] HoA | 2012-12-27 15:04:35 |
 További kellemes évvégét és évelejét mindenkinek!
Nem tudom, figyelembe vetted-e, és mert nem befolyásolja eredményeidet, egyszerűsítetted [1622] ábráját, minden esetre az S síkon a kétvesszős pontokat összekötő vonalak nem egyenes szakaszok.
[1617] metszet ábrájában persze a metsző sík O1 -en és O2 -n is áthalad, így az A'B' gömbi főkör ívet O2 -ből S-re vetítve egyenest kapunk. Ez azonban általában nem így van. A'B' az O1AB sík és G1 metszésvonala, G1 főköre. Ha ez nem megy át O2 -n, akkor a vetület S-en zárt görbe ( emlékezetem szerint kör ) lesz, melynek egy ívdarabja a háló A''B'' közötti vonala.
[1622] ábrája ígéretes, de még mindíg nem látok olyan állítást és annak bizonyítását, ami garantálná, hogy a végeredményül adódó kiterítésben nem lehet átfedés. Például: "P átforgatásakor az újonnan S-re érkező P csúcsok benne vannak a vetület megfelelő, esetleg összehúzásokkal már módosított tartományában". E'' jelöletlen szomszédját G'' -vel jelölve az összehúzás során mi lesz az E''G'' ívből? Egyenes szakasz? Vagy ha körív, akkor mekkora sugarú?
|
| Előzmény: [1622] bily71, 2012-12-26 23:24:30 |
|
| [1622] bily71 | 2012-12-26 23:24:30 |
 "Nem elemeztem a bizonyítást betűről betűre, de első ötletem az, nézd meg, mennyire igazak az összehúzásról elmondottak arra az Li'' lapra, melynek eredetijét, P poliéder Li lapját, az O1O2 szakasz átdöfi."
Átnéztem és átgondoltam. Az F fának a következő feltételeknek kell eleget tennie (F-et az egyszerűség kedvéért rajzolhatjuk közvetlenül P-re is).
(i) Az Li lapra (melyet az O1O2 egyenes döf) illeszkedő csúcs levél.
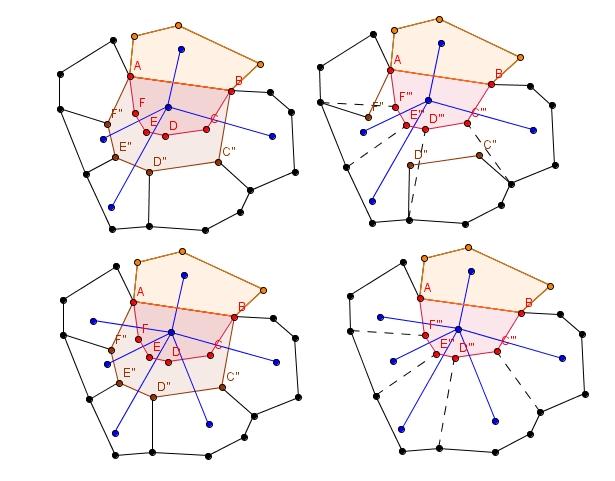
(ii) Létezik F1, F2, ..., Fm fa gráf sorozat úgy, hogy F1 egyetlen, az S síkkal párhuzamos L1 lapra illeszkedő csúcsból áll (ez legyen F gyökere), 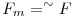 , továbbá Fk+1 úgy nyerjük Fk-ból, hogy kiválasztjuk Fk egy levelét (vagyis egy lapot, melyre Fk egy levele illeszkedik), majd összekötjük az összes olyan szomszédos lapra illeszkedő csúccsal, mely nem csúcsa Fk-nak. , továbbá Fk+1 úgy nyerjük Fk-ból, hogy kiválasztjuk Fk egy levelét (vagyis egy lapot, melyre Fk egy levele illeszkedik), majd összekötjük az összes olyan szomszédos lapra illeszkedő csúccsal, mely nem csúcsa Fk-nak.
Az ábrán (mely csak egy elképzelt esetet ábrázol) azt láthatjuk, mikor P-t átforgatjuk az AB élen, és az ABC''D''E''F'' lapot ráhúzzuk ABCDEF lapra. Az ábra felső részén látható, hogy ha nem (ii) szerint építjük fel F-et, akkor az összehúzás közben bár a összehúzott lap nem fed át egy lapot sem, de a megnyúlt szomszédainál felléphet átfedés, és nem tudhatjuk, hogy az megszűnik-e.
Az alsó részen módosítottuk F-et (ii) szerint, így a megnyúlt lapoknál sem lép fel átfedés. Most már kimondhatjuk, hogy az előbbi feltételeknek eleget tevő F szerint kiterítve P-t nem lép fel átfedés, és pont ezt akartuk megmutatni.
Amúgy kellemes ünnepeket! :)
|
 |
| Előzmény: [1620] HoA, 2012-12-23 16:24:41 |
|
| [1621] bily71 | 2012-12-23 20:44:42 |
 Igen, (ezt a "bizonyítást" a közzététel előtti álmatlan éjszakámon ötlöttem ki, csak úgy eszembe jutott) azon már a legelején gondolkoztam, hogy a "felső", vagyis az Li' lapot, amelyiket az O1O2 szakasz átdöfi, nem kellene hozzávenni a fához (ami így nem is, vagy hiányos feszítőfa), hanem utána biggyesztenénk oda az F* hiányos feszítőfa valamelyik levele után (de melyik után?), ugyanis ennek képe Li'' nem korlátos, nem világos, hogy mi történik vele az összehúzás közben, de később annyira nyilvánvalónak tűnt minden, hogy nem foglalkoztam vele.
Azonban úgy tűnik, hogy ha az Li'' nélküli sokszögre alkalmazzuk az összehúzást, akkor nem kapunk átfedést, még átgondolom, de annyira egyértelműnek tűnik.
|
| Előzmény: [1620] HoA, 2012-12-23 16:24:41 |
|
| [1620] HoA | 2012-12-23 16:24:41 |
 Én nem tudok, mivel eddig sohasem foglalkoztam ezzel a problémával, csak felszólításodra néztem bele. A "Dürer sejtés" Wikipedia oldalán azonban látható ez a hivatkozás:
http://www.ams.org/samplings/feature-column/fcarc-nets
Ebben megtalálhatod az alja felé a két következő idézetet:
"Her work related to finding a way of generating random 3-dimensional convex polyhedra and then choosing a random unfolding (not such simple issues) and seeing if the random unfolding overlapped. Her results showed that as the number of vertices of the solid increased, for a fixed specific solid the number of unfoldings where an overlap did occur increased" . ( Amiből itt csak az az érdekes, hogy növekvő csúcsszámmal növekszik azoknak a kiterítéseknek a száma, ahol átfedés van. ) És
"...no matter what reasonable type of tree Schlickenrieder picked, he was able to find examples of 3-dimensional convex solids where this tree did not lead to a net unfolding without overlaps." ( vagyis adott típusú fákat vizsgálva Sch.-nak sikerült olyan fát találni, mely nem vezetett átfedés nélküli kiterítésre )
A lényeg: A sejtés konvex poliéderekre sem azt mondja, hogy minden kiterítés átfedésmentes, hanem csak azt, hogy létezik átfedésmentes kiterítés. A Wikipédia cikk szerint "Dürer sejtette, hogy minden poliédert fel lehet vágni az élei mentén úgy, hogy lapjai (átfedés nélkül) kiteríthetőek legyenek a síkban, egy összefüggő sokszöget képezve." - és nem azt, hogy minden kiterítés ilyen.
Mivel te F megválasztására semmilyen különleges feltételt nem adtál meg, módszered az említett átfedéses kiterítéseket is létrehozná, tehát valahol a bizonyításban lehet a hiba. Nem elemeztem a bizonyítást betűről betűre, de első ötletem az, nézd meg, mennyire igazak az összehúzásról elmondottak arra az Li'' lapra, melynek eredetijét, P poliéder Li lapját, az O1O2 szakasz átdöfi.
|
| Előzmény: [1619] bily71, 2012-12-23 15:31:46 |
|
| [1619] bily71 | 2012-12-23 15:31:46 |
 Persze, hogy nem látod, mert a két sokszög ugyanaz. A különbség az út, hogy hogyan jutunk a sokszögig. Közvetlenül is felrajzolhatjuk H-t és F-et, majd szétvághatjuk, de attól még nem tudjuk, hogy lesz-e átfedés. Mutattam egy utat, ahol úgy kapjuk meg a sokszöget, hogy egyik lépésben sem keletkezik átfedés. Tulajdonképp azt próbálom demonstrálni, hogy H bármely F feszítőfája jó.
Most azért elbizonytalanítottál. Létezik olyan F, hogy a szétvágás és kiterítés során átfedést kapunk? Ha megkérlek, mutatnál erre példát?
|
| Előzmény: [1618] HoA, 2012-12-23 00:40:02 |
|
| [1618] HoA | 2012-12-23 00:40:02 |
 Nem látom, mi a különbség a módszereddel kapott síkbeli sokszög és aközött, hogy H-t - és így F-et - közvetlenül P-re rajzoljuk és P-t felvágjuk az F élei által nem metszett poliéder élek mentén. Vagyis kérlek mutass egy példát arra, ahol a két eredményül kapott sokszög különböző. Mert ha a két sokszög ugyanaz, akkor...
|
| Előzmény: [1616] bily71, 2012-12-21 22:42:34 |
|
| [1617] bily71 | 2012-12-22 23:07:33 |
 Azért több érdeklődést vártam. Ha jól tudom, a Dürer-sejtés még nyitott, Bezdek Dániel csak speciális estben bizonyította. Ha az előbbi megoldás jó, akkor én a poliéderek bővebb halmazán bizonyítottam.
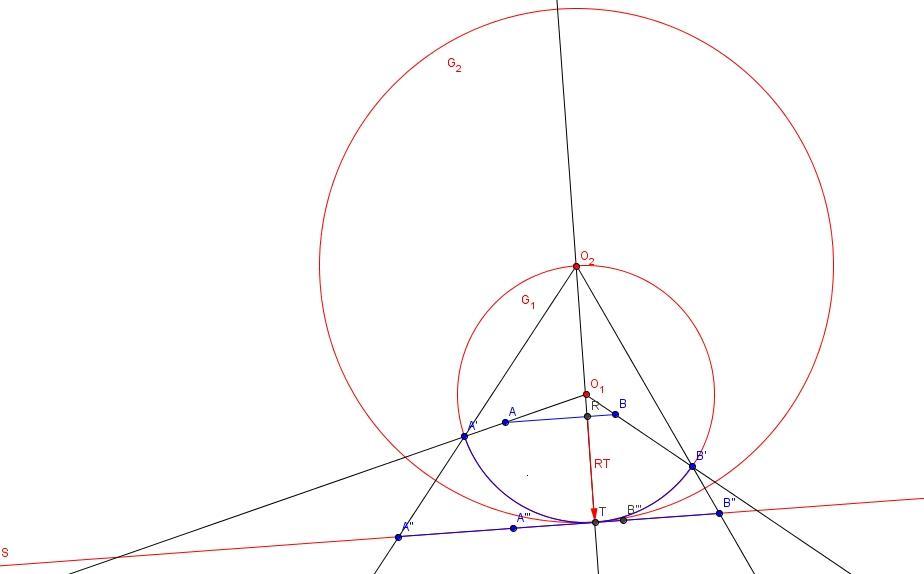
Készítettem egy ábrát, melyen két dimenziós metszetben P egy lapjára illeszkedő szakaszon mutatom be, hogy mit is csináltunk P-vel. Az AB szakaszt O1-ből G1 körre vetítjük, majd a kapott A'B' körívet O2-ből S-re invertáljuk, így kapjuk az A''B'' szakaszt. Ezek után eltoljuk AB-t 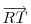 vektorral, kapjuk A1B1 szakaszt. Az A''B'' szakaszt ráhúzzuk A1B1-re, így kapjuk az A'''B''' szakaszt. Az AB és az A'''B''' szakaszok egybevágók. vektorral, kapjuk A1B1 szakaszt. Az A''B'' szakaszt ráhúzzuk A1B1-re, így kapjuk az A'''B''' szakaszt. Az AB és az A'''B''' szakaszok egybevágók.
Az A''B'' szakasz mindig nagyobb, mint az AB. Ugyanígy, mikor P-t görgetjük (elforgatjuk az éle, mint tengely körül), a görgetett lap mindig része a második képének, tehát összehúzást kell alkalmaznunk, hogy a harmadik kép egybevágó legyen az eredetivel. Az összehúzás során az átvágott élek mentén a szomszédos lapok eltávolodnak, vagyis rés keletkezik a síkon, így nem keletkezhet átfedés, a nem átvágott élek mentén pedig a szomszédos lap megnyúlik az összehúzás irányában, de átfedés itt sem keletkezik. Szemléletesen az történik, hogy felszabdaljuk az S síkot, majd az összehúzás transzformációval a síkrészeket ráhúzzuk P lapjaira, vagyis az egész S síkot ráképezzük P-re. (Ez nem egy szokványos transzformáció, hiszen két összehúzás között P-t ide-oda mozgatjuk.) Ez lenne a levezetés lényege. Kíváncsian várom a véleményeket.
|
 |
| Előzmény: [1616] bily71, 2012-12-21 22:42:34 |
|
| [1616] bily71 | 2012-12-21 22:42:34 |
 183. feladat. Adott P 3 dimenziós konvex poliéder. Terítsük ki P lapjait a síkba úgy, hogy átfedés nélkül egy összefüggő sokszöget alkossanak, azaz adjuk meg P egy hálóját!
Megoldás. Helyezzük P-t egy 3 dimenziós G1 gömbbe úgy, hogy az O1 gömb középpont P egy belső pontja legyen, továbbá P minden pontja G1 belső pontja legyen! Vetítsük P-t O1-ból G1 felszínére úgy, hogy ha Q pont P egy élének egy pontja, akkor Q' pont az O1Q egyenes és G1 felszínének metszete! Ekkor egy gömbre rajzolt P' gráfot kapunk.
Válasszuk ki P' minden lapjának egy belső pontját, (azaz a P' gömbre rajzolt gráf körei által határolt gömbfelszín tartományok egy belső pontját), majd kössük össze ezeket, ha két szomszédos lap, (azaz közös éllel rendelkező lapok) belső pontjai! Ekkor egy H gráfot kapunk. Legyen F H egy feszítő fája!
Sztereografikus projekciót alkalmazva képezzük P'-t és F-et az S síkra! S párhuzamos P egy lapjával, T pontban érinti érinti G1-et, ugyanitt érinti G2-t, az inverzió gömbjét, melynek O2 középpontja T átellenes pontja G1-en, továbbá O2 nem csúcsa P'-nek és F-nek, és nem illeszkedik P' és F egyik élére sem. Ekkor egy síkba rajzolt P'' gráfot és egy F' fát kapunk.
Legyen az R pont P, az S síkkal párhuzamos, L1 lapja és az O1T egyenes metszete! Toljuk el P-t az 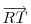 vektorral! Ekkor L1 eltolt képe illeszkedik S-re. vektorral! Ekkor L1 eltolt képe illeszkedik S-re.
Gondoljunk S-re úgy, mint vastagság nélküli rugalmas, vágható anyagból álló felületre! Vágjuk át S-t azon élek mentén, melyeket nem metsz F' egyik éle sem!
Legyen az L1 lap egy csúcsa V1, húzzuk bele V1''-t V1-be! Ismételjük ezt L1'' minden csúcsával! Az "összehúzás" transzformáció után L1'' képe egybevágó lesz L1-gyel, hisz fedik egymást.
Gördítsük át az eltolt P-t az egyik élén az S síkon az F' fa egy éle mentén, vagyis P egy olyan élén, mely metszi F' egy élét. Ekkor az L2 lap illeszkedik S-re, úgy, hogy az L1,L2 lapok közös éle fedi az összehúzott L1'' és a félig összehúzott L2'' lapok közös élét, továbbá L2 része L2''-nek. Legyen V2 az L2 lap egy csúcsa! Húzzuk bele V2''-t V2-be! Ismételjük ezt L2'' minden csúcsával! Az összehúzás után L2'' képe fedi L-2-t, így azok egybevágók. Az összehúzott L1'',L2'' lapok nem fedik át egymást. Az összehúzott L2'' nem fedi át egyik vele szomszédos másik lapot sem, hiszen vagy át van vágva az S sík a közös él mentén, így inkább távolodott szomszédjától, mivel az helyben maradt, vagy a közös élt metszi F'-et, ekkor nem keletkezik átfedés.
Gördítsük végig P-t F' minden útján az utak valamilyen sorrendjében! Egy út végére érve gördítsük visszafelé az úton P-t, míg az L1 lap nem illeszkedik újra S-re! Minden gördítés során alkalmazzuk az összehúzás transzformációt!
F' minden útját végigjárva egy összefüggő sokszöget kapunk, mely sokszög P lapjaival egybevágó sokszögekből áll, így a sokszög területe és P felszíne egyenlő, vagyis eleve kizárt, hogy a gördítések során átfedés keletkezett. Az S sík átvágása miatt az összehúzás során megkettőződött éleket újból fedésbe hozva P-vel egybevágó poliédert kapunk (a sokszögből visszahajtogathatjuk P-t), vagyis a feladatot sikerült megoldanunk.
P tetszőleges volt, ezért a feladatot megoldva egyúttal konstruktív bizonyítást adtunk Dürer sejtésére abban az esetben, ha a poliéder konvex.
Boldog Világvégét! :)
|
|
| [1615] w | 2012-12-12 17:59:04 |
 Ez is szép megoldás.
A feladat bemutatja, hogy több ismerettel sokkal bonyolultabban oldanánk meg egy nem nyilvánvaló általános iskolás feladatot, mint egy korlátos ismerettel rendelkező nyolcadikos. (Persze az más kérdés, hogy egy általános iskolás mit tesz, ha egy trigonometrikus egyenletet kellene fejtegetni.) Akinek elemi geometriával van dolga, annak állandó gyakorlásra van szüksége, hogy ezekhez való érzékét fenntartsa. (Megjegyzendő, hogy mindenhol van kivétel.)
A feladat megoldása:
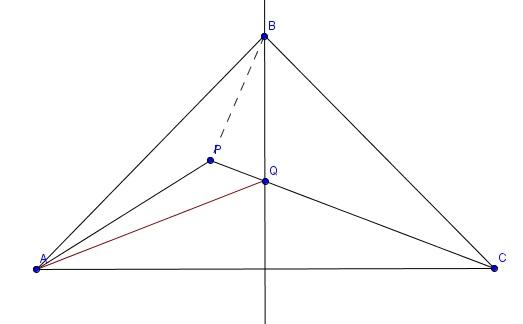
Célszerű az egyenlő szárúságot kihasználni. Rajzoljuk be a háromszög szimmetriatengelyét, ez messe CP-t Q-ban, ekkor QAC<=ACQ<=30°. Vegyük észre, hogy AP felezi a BAQ<-et, ráadásul PQ az AQB< felezője. Így P az AQB háromszög beírt körének középpontja, azaz BP felezi ABQ<-et. BPC<=180°-(80°/2+80°/4)-(50°-30°)=100°.
Ez egyszerű volt. Kis túlzással annyi kellett hozzá, hogy észrevesszük, hogy az egyenlő szárú háromszög szimmetrikus. Aki erre rákényszerítené a szabályos 18-szöget, az azért teszi, mert a feladatot ennél összetettebbnek képzeli, és jogosan. Tehát ajánlom a feladatok egyszerű megközelítését (aki elolvasta a bemutatkozásomat, az el is várhatja a könnyebb példákat :).
Megint más kérdés, hogy milyen a feladat általánosítása...
|
 |
| Előzmény: [1614] HoA, 2012-12-11 13:07:32 |
|
| [1614] HoA | 2012-12-11 13:07:32 |
 Hogy mennyire tömény és elegáns, azt ítélje meg más, minden esetre "nyolcadikosabb" , mint az előző.
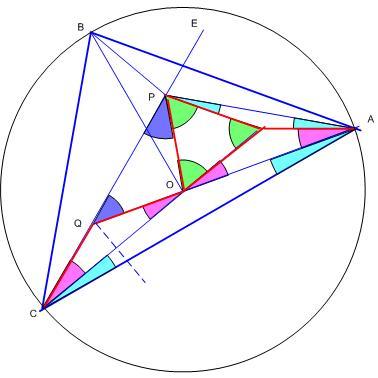
Építsük fel a mellékelt ábrát az ABC háromszög csúcsaiból, a körülírt kör O középpontjából és a CA oldallal 30 fokos szöget bezáró CE egyenesből kiindulva. CO felező merőlegesének és CE -nek a metszéspontja Q. Az állandó QC hosszúságú piros szakaszok ismételt felméregetésével kialakul az ábra. A 10, 20, 40 ill. 60 fokos szögeket kékkel, rózsaszínnel, lilával ill. zölddel jelöltem. Látható - és persze bizonyítható - , hogy P a feladatban definiált pont.
A BPC háromszöget O körül pozitív irányban 100 fokkal elforgatva P Q-ba , B C-be kerül, A BP szakasz képe tehát a PC-vel egy egyenesbe eső CQ, ezért BPC szög 100 fok.
|
 |
| Előzmény: [1611] w, 2012-12-10 16:46:48 |
|
| [1613] w | 2012-12-10 22:22:18 |
 Jogos a hozzászólásod. Én arra gondoltam, hogy a feladatot úgy is meg lehet oldani, hogy csak a következőket használhatjuk: háromszög belsőszög-összege, nevezetes vonalai, beírt kör, szög/szakasz/pont felvétele.
A Fálesz-HoA-megoldás sokkal hasznosabb, mint az, amire gondolok. Mindenesetre hamarosan - amint lesz időm az ábrát elkészíteni - közlöm a megoldásomat.
******
Mutassuk meg, hogy ha egy háromszög két belső szögfelezője azonos hosszú, akkor és csak akkor a háromszög egyenlő szárú.
|
| Előzmény: [1612] Lóczi Lajos, 2012-12-10 18:30:06 |
|
|
| [1611] w | 2012-12-10 16:46:48 |
 Köszönöm szépen, a megoldásotok nagyon szép, és igen sok feladatra felhasználható.
A feladatot eredetileg nyolcadik osztályosoknak tűzték ki, talán 2007-ben (?), ezért nyilván van olyan megoldás, ami tömény, elegáns háromszöggeometria.
|
| Előzmény: [1610] HoA, 2012-12-10 11:26:43 |
|
| [1610] HoA | 2012-12-10 11:26:43 |
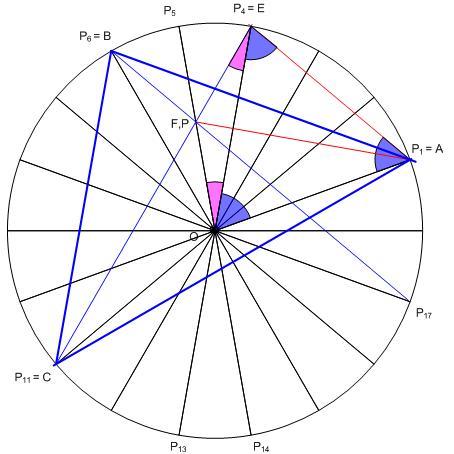
 A [1609] –beli megközelítés egy konkrét megvalósítása, a szükséges nem triviális közös metszéspont bizonyításával: Válasszuk meg az A, B, C csúcsokat az ábra szerint, így ABC a feladatban szereplő háromszög. Mivel egy sokszög oldalhoz, ill. a körülírt körben a hozzá tartozó ívhez 10 fokos kerületi és 20 fokos középponti szög tartozik, AOC  = 160 fok , így CAO = 160 fok , így CAO  = 10 fok. A CA –val 30 fokos szöget bezáró P11P4 ( = CE ) , egyenes és a P5P14 átmérő metszéspontja legyen F. Az OEF háromszögben OEF = 10 fok. A CA –val 30 fokos szöget bezáró P11P4 ( = CE ) , egyenes és a P5P14 átmérő metszéspontja legyen F. Az OEF háromszögben OEF  = 20 fok, mint a P11P13 ívhez tartozó kerületi szög, FOE = 20 fok, mint a P11P13 ívhez tartozó kerületi szög, FOE  = 20 fok, mint a P4P5 –höz tartozó középponti szög, OEF háromszög egyenlőszárú. Az AOE egyenlőszárú háromszögben O-nál 60 fokos szög van, mint P1P4 –hez tartozó középponti szög, AOE háromszög szabályos. AEFO deltoid, AF átlója felezi a 60 fokos OAE szöget, FAO = 20 fok, mint a P4P5 –höz tartozó középponti szög, OEF háromszög egyenlőszárú. Az AOE egyenlőszárú háromszögben O-nál 60 fokos szög van, mint P1P4 –hez tartozó középponti szög, AOE háromszög szabályos. AEFO deltoid, AF átlója felezi a 60 fokos OAE szöget, FAO  = 30 fok, FAC = 30 fok, FAC  = 40 fok , F tehát feladatunk P pontja. Mivel P rajta van a P5P14 átmérőn és a P11P4 átlón, ezért az utóbbinak P5P14 –re vett tükörképén , a P6P17 átlón is rajta van. A BCP háromszögben BCP = 40 fok , F tehát feladatunk P pontja. Mivel P rajta van a P5P14 átmérőn és a P11P4 átlón, ezért az utóbbinak P5P14 –re vett tükörképén , a P6P17 átlón is rajta van. A BCP háromszögben BCP  = P6CP4 = P6CP4 = 20 fok, CBP = 20 fok, CBP  = P11BP17 = P11BP17 = 60 fok, így BPC = 60 fok, így BPC  = 100 fok. = 100 fok.
|
 |
| Előzmény: [1609] Fálesz Mihály, 2012-12-10 09:28:23 |
|
| [1609] Fálesz Mihály | 2012-12-10 09:28:23 |
 Az ilyenfajta feladatokhoz egy kiváló cikk: Csirmaz László: Egy geometriai feladatról
A lényeg röviden:
1. Egy szabályos 18-szögben az átlók közötti szögek mind a 10o többszörösei.
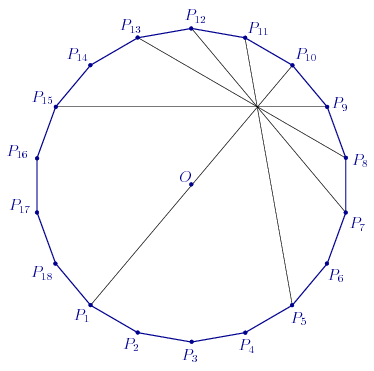
2. Vannak olyan átlók, amik nem teljesen triviálisan egy ponton mennek át. Például a O középpontú P1P2...P18 szabályos 18-szögben a P9P15 átló az OP12 sugár felező merőlegese, és ebből következik, hogy a P1P10 egyenes tükörképe a P9P15 átlóra éppen a P7P12 egyenes. Ha ezeket a P1P10 átmérőre is tükrözzük, láthatjuk, hogy a P1P10, P5P11, P7P12. P8P13 és P9P15 átlók egy ponton mennek át.
3. A feladat megoldása ezek után abból áll, hogy megkeressük a rengeteg oldal és átló között a feladat ábráját...
|
 |
| Előzmény: [1608] w, 2012-12-09 11:22:59 |
|
|
|
| [1606] w | 2012-12-08 21:34:35 |
 ABC háromszögben AB=AC, P belső pontra PAC<=40 fok, ACP<=30 fok. Mekkora a BPC<, ha ABC<=80 fok?
|
|
|
|
| [1603] Mordon | 2012-10-31 15:00:07 |
 P az ABC háromszög belső pontja. A CP egyenes az AB oldalt a D, az AP egyenes a BC oldalt az E, a BP egyenes a CA oldalt az F pontban metszi. Tudjuk, hogy PA+PB+PC=43 és PD=PE=PF=3. Határozzuk meg a PA.PB.PC szorzat értékét.
Ennek a tavalyi Szőkefalvi feladatnak a megoldását valaki le tudná írni?
Előre is köszönöm!
|
|
|
| [1601] HoA | 2012-10-24 13:02:31 |
 Gondolom mivel a szereplő betük közül N a B mellett van a billentyűzeten, a kérdező B-t gondolt. Ekkor a metszéspont Jónás T pontja, a keresett hosszúságok AT = 4/5 AC = 4/5 * 28 cm = 22.4 cm, BT = 3/5 BC = 3/5 * 21 cm = 12.6 cm , mint [1597]-ben.
|
| Előzmény: [1596] jonas, 2012-10-23 22:01:37 |
|
|










 = 160 fok , így CAO
= 160 fok , így CAO 



