| [1703] w | 2013-05-14 19:18:04 |
 Szerintem hasonló jellegű a belinkelt feladat. Talán a Steiner-tételt erre is rá lehetne nyomni? A másik az - amit gondolom észrevettél -, hogy hiperbolát invertálva és az alapkört mozgatva mindenféle szép őscsigát kaphatunk :-)
|
| Előzmény: [1702] Sinobi, 2013-05-14 17:38:05 |
|
| [1702] Sinobi | 2013-05-14 17:38:05 |
 felvettem az OB-n levő középpontú, O-n átmenő apollóniusz-köröket, leinvertáltam az ábrát O-ra, kaptam a következő feladatot:
Adott egy egyenesen B, O, rögzített, és egy F futópont. Adott az egyenesen kívül egy A pont. Hol lesz az FOA kör, és az FBF egyenes (BF felezőmerőlegese) metszéspontja? Geogebrában megnéztem, merőleges hiperbolának néz ki. Feladat: bizonyítsd be a sejtést, vagy cáfold (adj meg 6 metszéspont koordinátát úgy, hogy nem lesznek merőleges hiperbolán)
|
 |
| Előzmény: [1679] ibiro, 2013-04-05 13:09:20 |
|
| [1701] Maga Péter | 2013-05-02 08:18:47 |
 Általában nem mondhatjuk. Elnézést, ebből a szempontból az [1697]-ben leírt példa túl speciális volt, ahol véletlenül ez is igaz. De ugyanott legyen inkább a görbe f(t)=k(t2). Ekkor f'(t)=2tk'(t)=k(t)2tk'(0): itt a k(t) a csoportelem, amivel eltoljuk a 2tk'(0) Lie-algebra elemet (ami csak t=0-ban egyenlő f'(0)-val, f' látványosan nem invariáns). A képlet nem mondja azt, hogy a görbe érintője maga invariáns vektormező, az invarianciát csak a TeG és a TgG érintőterek természetes azonosításához használjuk.
Másképpen: azt nem tehetjük fel, hogy a görbe érintője (a mozgó pont sebessége) invariáns, de azt igen, hogy minden egyes pontban illeszkedik egy invariáns vektormezőre (ez persze lehet minden pontban más és más). Tehát a képletbeli gX érintő nemcsak az eltoláson keresztül függ g-től, hanem maga az X is mutat(hat) g-függést, ld. a fenti f(t)=k(t2) példát, ahol gyorsulva járjuk be a körvonalat.
|
| Előzmény: [1700] Lagrange, 2013-05-01 17:25:23 |
|
| [1700] Lagrange | 2013-05-01 17:25:23 |
 Na most már majdnem teljesen világos. A mozgás kijelöl egy görbét a Lie-csoporton, ennek a görbének a sebességét pedig egy X vektormezőnek tekintjük, ami egy adott g pontban a g görbe szerinti deriválás, tehát X(g)=dg/dt. Csak annyi a kérdés, hogy miért mondhatjuk a sebesség vektormezőre (ami matematikailag a görbe érintője) hogy az balinvariáns?
|
| Előzmény: [1699] Maga Péter, 2013-04-30 09:03:37 |
|
| [1699] Maga Péter | 2013-04-30 09:03:37 |
 ,,Ez a Lie-algebra definíciója, vagy az Exponenciális leképezéshez és a Hausdorff-Campbell formulához van köze? Vagy arról van szó, hogy egy vektormezőt egyértelműen meghatároz egy pontban felvett értéke?'' Hát, igazából minden mindennel összefügg, ahogy mondani szokás:). De a formulához a második mondatod a kulcs: ,,egy invariáns vektormezőt egyértelműen meghatároz egy pontban felvett értéke'' (természetesen ez nem igaz minden vektormezőre).
A wikipediás leírás szerintem használható, neked főleg a leképezés deriváltjáról szóló bekezdés kell, a leképezésed az Lg-1 eltolás.
|
| Előzmény: [1698] Lagrange, 2013-04-30 03:40:23 |
|
| [1698] Lagrange | 2013-04-30 03:40:23 |
 Köszönöm a választ.
Igazából az előre tolást meg visszahúzást értem, csak azt nem értem, hogy ez a képlet hogy jön ki. Ez a Lie-algebra definíciója, vagy az Exponenciális leképezéshez és a Hausdorff-Campbell formulához van köze? Vagy arról van szó, hogy egy vektormezőt egyértelműen meghatároz egy pontban felvett értéke? Szóval sokat olvastam erről a témáról, de nem áll össze a kép :S
Egy merev test mozgásának differenciálegyenletét kéne ennek segítségével levezetni, úgy, hogy a pályája a Lie-csoporton egy görbe, a sebessége meg a Lie-algebrájának egy eleme.
|
| Előzmény: [1697] Maga Péter, 2013-04-29 10:22:55 |
|
| [1697] Maga Péter | 2013-04-29 10:22:55 |
 Ha jól sejtem, ezzel az előretolás-vissahúzás dologgal vannak nehézségeid. Konkrét példák sokat tudnak segíteni, egy nagyon egyszerűt le is írok.
Legyen
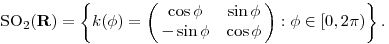
Modulo 2 számolva k( számolva k( )k( )k( )=k( )=k( + + ). Most vegyük fel ezen a t ). Most vegyük fel ezen a t k(t),(t k(t),(t [0,2 [0,2 ]) görbét. Ennek deriváltja a k(t) pontban: ]) görbét. Ennek deriváltja a k(t) pontban:
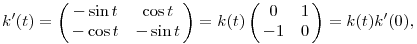
ahol k'(0) már a Lie-algebra eleme:
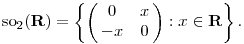
(A Lie-algebrát általában gót betűkkel jelöljük, de a fórum TeX-je nem érti a frak és mathfrak parancsok egyikét sem, ezért a kisbetű.)
Magyarán: vesszük az érintőt, visszahúzva az egységelembe megkeressük a neki megfelelő Lie-algebra elemet, majd azt előretoljuk. A kérdéses képlet csak ennyit mond.
|
| Előzmény: [1696] Lagrange, 2013-04-29 03:02:33 |
|
| [1696] Lagrange | 2013-04-29 03:02:33 |
 Üdv! Remélem valaki képen van differenciálgeometria terén. Arról lenne szó, hogy egy Lie-csoporton való mozgást kéne leírni differenciálegyenlettel. Konkrétan azt nem értem, hogy a (dg/dt)=gX egyenlet hogy jön ki. A képletben g eleme a Lie csoportnak, X meg a Lie algebra eleme, tehát egy vektormező, amit ugye úgy kapunk, hogy vesszük az egységelemnél az érintő térnek egy elemét. Eddig ahol olvastam visszahúzásokról (pullback) meg előretolásokról (pushforward) volt benne szó, de nem sikerült megértenem. Küldök egy képet is, hogy miről is van szó.
|
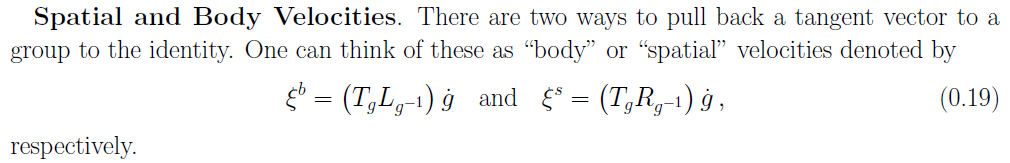 |
|
| [1695] Sinobi | 2013-04-28 00:34:29 |
 ,,Már látjuk, hogy nem lesz valami szép végeredmény"
Hé! Nekem tetszik!
Észrevehetted volna, hogy a kör tháleszkör, és az FDA< derékszög, így FDA ~ BFA.
felírva, hogy szögfelezőtétel: 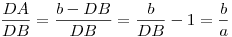 tehát tehát 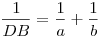
A hasonló derékszögű háromszögek miatt (befogótétel?): 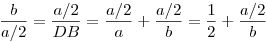
és ebből már szépen látszik is, hogy 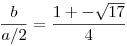
Ugyanilyen: ha egy háromszög egyik szöge derékszög, akkor a másik kettőt nem lehet úgy megválasztani, hogy a szögfelezőkre rakott kör átmennyen egy csúcson (megfigyelés). Bizonyítsd be a megfigyelést. Mekkora lehet egy háromszögben egy adott szög maximuma, hogy a másik kettőből lehessen alkotni Sinobi-tipusú háromszöget?
Két különböző eset, hogy a csúcson átmegy, vagy nem megy át a kör, nem tudom melyik milyen nehéz (megoldhatók-e egyáltalán elvadult koordinátázás nélkül).
|
| Előzmény: [1694] w, 2013-04-26 22:16:11 |
|
| [1694] w | 2013-04-26 22:16:11 |
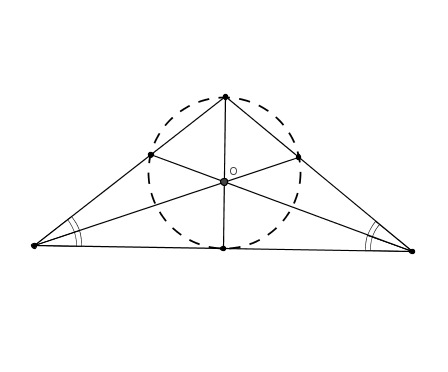
 Szép kis egyszerű feladat, kis ötlet kell hozzá. Ezért le is lőném. A szöveg kihagyja, de az ábrából felteszem, hogy a szárszög csúcsa van rajta a gondolt körön. Megjegyezném, hogy amúgy csak ez a csúcs lehet rajta.
Betűzzük le: legyen ABC a háromszög, ahol AB=AC=b és BC=a hosszú. Legyenek a szögfelezők talppontjai D AB, E AB, E AC, F AC, F BC. Szimmetria miatt a szereplő k kör érinti a BC alapot. Másrészt szögfelezőtétel miatt AD/DB=AE/EC=b/a, vagyis ráadásul BC. Szimmetria miatt a szereplő k kör érinti a BC alapot. Másrészt szögfelezőtétel miatt AD/DB=AE/EC=b/a, vagyis ráadásul 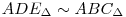 . Az ötlet az, hogy nagyítsuk ADE-t . Az ötlet az, hogy nagyítsuk ADE-t  =(a+b)/b aránnyal A-ból ABC-be, ekkor k képe ABC körülírt köre lesz, melynek átmérője =(a+b)/b aránnyal A-ból ABC-be, ekkor k képe ABC körülírt köre lesz, melynek átmérője 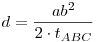 ismert képlet szerint. AF képe pont egy átmérő lesz, ahol AF az ABC háromszög magassága: AF=2tABC/a. Tehát felírható, hogy: ismert képlet szerint. AF képe pont egy átmérő lesz, ahol AF az ABC háromszög magassága: AF=2tABC/a. Tehát felírható, hogy:
d=AF.
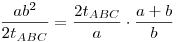
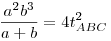 . .
Már látjuk, hogy nem lesz valami szép végeredmény, GeoGebra szerint ABC< kb. 38,7° lesz (ha megszerkesztjük). Akkor legyen az alapon fekvő szög x, a trigonometrikus területképletet behelyettesítve:
a2b3/(a+b)=a2b2sin2x
b=(a+b)sin2x
b=(2bcos x+b)sin2x
1=(2cos x+1)(1-cos2x)
Hát ha trigonometrikus egyenlet, akkor oldjuk is meg:
1=2cos x-2cos3x+1-cos2x
2cos3x+cos2x-2cos x=0
Új ismeretlen: y=cos x.
y(2y+y-2)=0
Mivel 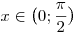 , ezért y=0 nem gyök. A másodfokú tag diszkriminánsa 17, gyökei , ezért y=0 nem gyök. A másodfokú tag diszkriminánsa 17, gyökei 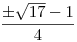 , ahol a pozitívra lesz szükség: , ahol a pozitívra lesz szükség: 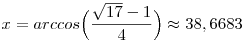 . (A könnyű érthetőség kedvéért szögben adom meg.) . (A könnyű érthetőség kedvéért szögben adom meg.)
Kitűnik még, hogy cos x szerkeszthető, ezért ABC háromszög is.
|
| Előzmény: [1693] Sinobi, 2013-04-26 20:11:26 |
|
| [1693] Sinobi | 2013-04-26 20:11:26 |
 Másik feladat: mekkorák annak az egyenlőszárú háromszögnek a szögei, ahol a szögfelezők talppontjaira illesztett kör átmegy a háromszög csúcsán?
|
 |
|
| [1692] Sinobi | 2013-04-26 20:08:45 |
 Borzasztó sok olyan görbe létezik, amin rajta van egy (na jó, kettő) meghatározott pont. :) Egyre kevésbé hiszem azt, hogy a feladatod megszerkeszthető, lehet, hogy létezik szép megoldás mondjuk vonalzóeltolással, fapálcikákkal, kötél és rajzszög alapú ellipsziszővel etc. de nem látok ilyet.
|
|
| [1691] ibiro | 2013-04-26 12:31:40 |
 "Mivel M1 ill M2 ellipszis pontok, nem kell bizonyítani, hogy MA + MB állandó ( az adott ellipszisen ) hisz ez az ellipszis definíciójából következik" ... de honnan veszed hogy ellipszis pontok - ez csak a te feltételezésed ! Bízonyisd be és akkor elhiszem.
Sinobi [1680] szerint egy "csúnya csigabigán", szerinted egy "elfajult ellipszisen" , szerintem pedig egy hurkon és egy parabolán vannak. Igaza van-e valakinek ??? Addig senkinek amig nem jön bízonyitással.
|
 |
| Előzmény: [1690] HoA, 2013-04-25 11:21:01 |
|
| [1690] HoA | 2013-04-25 11:21:01 |
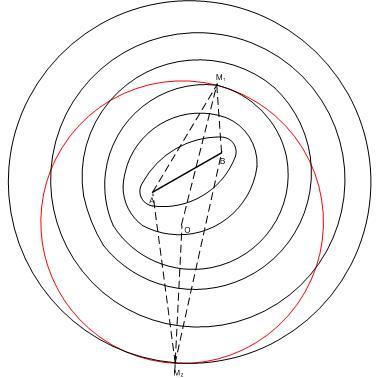
 A körön belüli általános helyzetű A és B pontokhoz mint fókuszokhoz tartozó ellipszisek az AB szakasztól, mint elfajult ellipszistől az "AB felezőpontja körüli nagyon nagy sugarú majdnem-kör" -ig ( elnézést a pongyola fogalmazásért ) folytonosan nőnek a nagytengely folyamatos növelésével. A legkisebbeknek nincs közös pontjuk a körrel. Lesz egy olyan, melynek egy közös pontja van a körrel, ez M1, ezután lesznek olyanok, melyeknek több közös pontjuk van a körrel. Eljutunk egy olyan nagy ellipszisig, melynek ismét csak egy közös pontja lesz a körrel M2 . Mivel M1 ill M2 ellipszis pontok, nem kell bizonyítani, hogy MA + MB állandó ( az adott ellipszisen ) hisz ez az ellipszis definíciójából következik. Talán csak annyiban kell szigorítani a fenti gondolatmenetet, hogy belássuk: ha egy körnek és egy ellipszisnek csak egy közös pontja van, akkor az érintési pont és így az itt húzott érintő egyenesek azonosak. Ebből már következik a feladat feltételének teljesülése.
|
 |
| Előzmény: [1689] ibiro, 2013-04-25 08:09:39 |
|
| [1689] ibiro | 2013-04-25 08:09:39 |
 Ehhez kellene bizonyitani hogy MA+MB állandó, de mi van akkor ha az ellipszis a kör belsejében lesz és nem érinti a kört ? A feladat nem mond semmit a kör és a szakasz helyzetéről.
|
| Előzmény: [1688] HoA, 2013-04-24 13:18:49 |
|
|
|
|
|
| [1684] Kemény Legény | 2013-04-20 19:06:18 |
 A koszinusztételes megoldást kicsi jobban "be lehet csomagolni" vektorok (és azok skaláris szorzatának) használatával. Ha az OA,OB,OC,OD,OP vektorokat rendre a,b,c,d,p jelöli, akkor
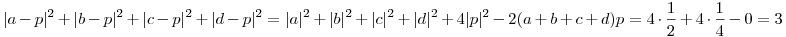 , mert a+b+c+d=0. , mert a+b+c+d=0.
|
| Előzmény: [1683] Layven, 2013-04-20 18:47:24 |
|
| [1683] Layven | 2013-04-20 18:47:24 |
 Igen, ez lehetőségként végig megvolt bennem, de az nem lett volna szép megoldás. Végül sikerült megoldani koordináták nélkül.(ABCD négyzet csúcsai, O a középpontja,P a kiválasztott pont a beírt körön.)
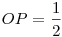 , , 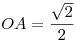
Koszinusztétel az AOP háromszögben:
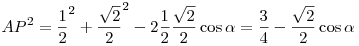
Felírva mindegyik oldalt hasonlóképpen és összegezve:
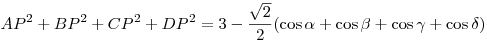
Most megmutatjuk, hogy a koszinuszok összege 0. A, O és C pontok egy egyenesben vannak, tehát AOP +POC +POC =180o, azaz =180o, azaz  + + =180o, hasonló módon pedig =180o, hasonló módon pedig  + + =180o =180o
Ismert, hogy 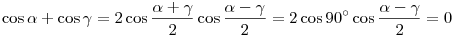
Hasonló módon kijön,hogy cos  +cos +cos  =0, tehát a koszinuszok összege valóban 0, vagyis AP2+BP2+CP2+DP2=3 =0, tehát a koszinuszok összege valóban 0, vagyis AP2+BP2+CP2+DP2=3
|
| Előzmény: [1682] Sinobi, 2013-04-20 12:32:17 |
|
| [1682] Sinobi | 2013-04-20 12:32:17 |
 Próbáld koordinátákkal. Vegyél fel egy P(Xp,Yp) pontot, és számold ki egy (mondjuk origó középponttú) egységnégyzet csúcsaitól a távolságnégyzetek összegét.
|
| Előzmény: [1681] Layven, 2013-04-20 11:32:22 |
|
| [1681] Layven | 2013-04-20 11:32:22 |
 A következő problémán akadtam fent: Bizonyítsuk be, hogy ha ABCD egységnégyzet beírt körén lévő pont P, akkor AP2+BP2+CP2+DP2=3
|
|
| [1680] Sinobi | 2013-04-13 19:10:10 |
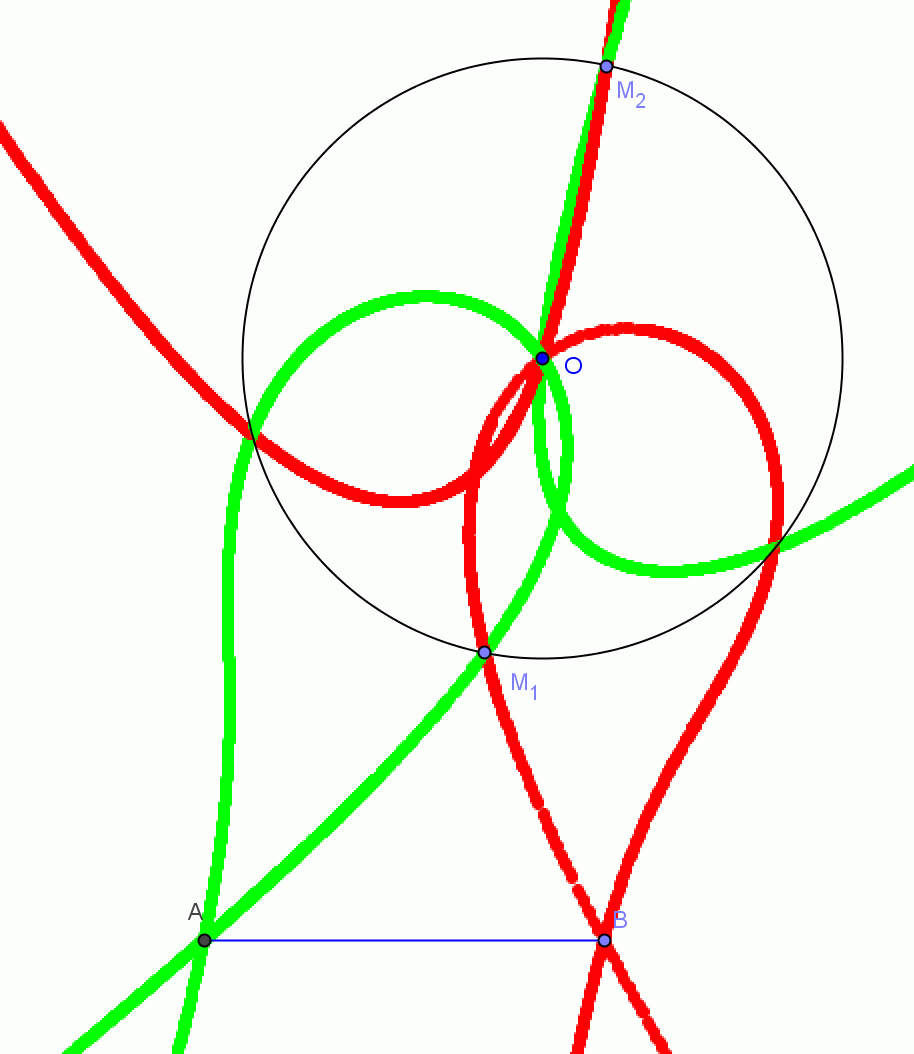
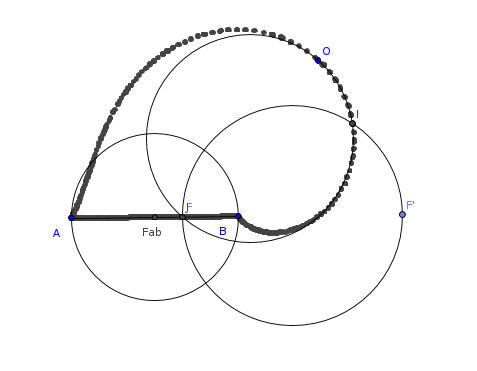
 Az olyan I pontok halmaza, ahol I rajta van AB F-hez tartozó szögfelezőkörén, és az FO tháleszkörén, (azaz AIB szögfelező talppontja F és FIO merőleges) egy csúnya csigabigán vannak. Kérdés: igaz-e, hogy ha meg tudjuk szerkeszteni valahogy a csúnya csigabiga és minden O középponttú kör metszéspontjait, akkor a csúnya csigabiga és egy tetszőleges kör ill. és egy tetszőleges egyenes metszéspontjait is.
|
 |
| Előzmény: [1679] ibiro, 2013-04-05 13:09:20 |
|
| [1679] ibiro | 2013-04-05 13:09:20 |
 Adott az AB szakasz és az O középpontú R sugarú kör. Határozzuk meg azt az M pontot (pontokat) a körön melyre az OM egyenes az AMB szög szögfelezője.
|
|







 számolva k(
számolva k( )k(
)k( )=k(
)=k( k(t),(t
k(t),(t [0,2
[0,2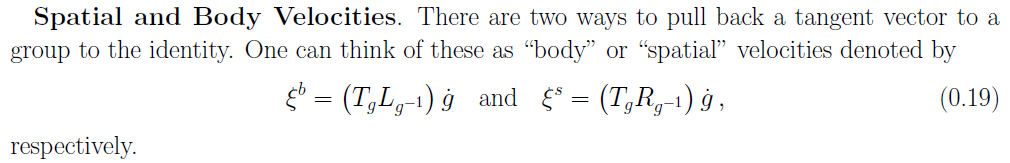
 =(a+b)/b aránnyal A-ból ABC-be, ekkor k képe ABC körülírt köre lesz, melynek átmérője
=(a+b)/b aránnyal A-ból ABC-be, ekkor k képe ABC körülírt köre lesz, melynek átmérője 





 +POC
+POC +
+ +
+ =180o
=180o 