| [387] axbx | 2006-03-13 20:48:33 |
 Nem megy nékem az geometria..
|
|
| [386] HoA | 2006-03-10 16:17:31 |
 Köszönöm az ábrát.
Legyen az AB átmérőjű f félkör középpontja O, sugara R. F rajta van f A-ból vett 1/2 arányú kicsinyítésén vagyis az AO átmérőjű f2 félkörön. n hossza A pont k-ra vonatkozó hatványának négyzetgyöke. Az AF távolságot d-vel, k sugarát r-rel jelölve n2=(d+r)(d-r)=d2-r2 . C-t - és ezzel F-et és d-t - rögzítve ez akkor a legnagyobb amikor r a legkisebb, vagyis amikor k belülről érinti f-et. Ekkor D az OF egyenes és f metszéspontja, jelöljük Dm-mel.
C-t az f félkörön mozgatva, C és F helyzetét a 0 és  közé eső BAC = OAF = közé eső BAC = OAF =  szöggel jellemezve, mivel F rajta van OA Thalesz-körén szöggel jellemezve, mivel F rajta van OA Thalesz-körén
d=Rcos ,r=R(1-sin ,r=R(1-sin ) )
n2=R2(cos2 -(1-sin -(1-sin )2)=R2(cos2 )2)=R2(cos2 -1-sin2 -1-sin2 +2sin +2sin )=R2(cos2 )=R2(cos2 -cos2 -cos2 -sin2 -sin2 -sin2 -sin2 +2sin +2sin )= )=
=2R2(sin -sin2 -sin2 )=2R2(sin )=2R2(sin )(1-sin )(1-sin ) )
Ez pedig a számtani és mértani közép egyenlőtlenség miatt akkor a legnagyobb, ha sin =1-sin =1-sin =1/2 Ez a vizsgált tartományban =1/2 Ez a vizsgált tartományban  =30o -nál következik be. Így DOA szög = CBA szög = 60o , A, D, C és B pontok egy szabályos hatszög egymás utáni csúcsai. sin =30o -nál következik be. Így DOA szög = CBA szög = 60o , A, D, C és B pontok egy szabályos hatszög egymás utáni csúcsai. sin =1/2 -t helyettessítve =1/2 -t helyettessítve 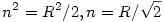
|
 |
| Előzmény: [385] BohnerGéza, 2006-03-09 20:26:52 |
|
|
| [384] HoA | 2006-03-09 17:53:28 |
 - Az én értelmezésemben a rögzített AB átmérőjű félköríven C és D csak ACDB vagy ADCB sorrendben lehetnek.
- F az AC szakasz vagy az AC ív felezőpontja?
|
| Előzmény: [382] BohnerGéza, 2006-03-09 12:15:40 |
|
|
| [382] BohnerGéza | 2006-03-09 12:15:40 |
 68. feladat: C és D a rögzített AB átmérőjű félköríven vannak ABCD sorrendben. Legyen F az AC felezőpontja, k az F középpontú, D-n átmenő kör és n az A-ból k-ig húzott érintőszakasz. Hol van C és D, ha n a lehető leghosszabb? Mekkora ekkor n? (AB-hez képest.)
|
|
| [381] hobbymatekos | 2006-03-08 14:48:24 |
 Sziasztok. Én úgy gondolom: a szabályos háromszög oldallapok súlypontjaiba a lapok területével azonos skalárok (mint tömeg pontrendszer) tömegközéppontjában lesz a tetraéder súlypontja. (Vagyis a statikai nyomatékok vektorainak bármely geometriai pontra számitott eredő nyomaték vektorának a súlypontba redukáltja nullvektor.)
|
| Előzmény: [378] BohnerGéza, 2006-02-23 23:30:05 |
|
| [379] axbx | 2006-02-27 16:34:28 |
 Már a véleményemet se mondhatom el.. (Fődmívelö) Azért nem vót szép, hogy bannoltak.
Na csak Az lenne a kérdésem, hogy hogyan kell bizonyítani a kör egyenletét?
|
|
| [378] BohnerGéza | 2006-02-23 23:30:05 |
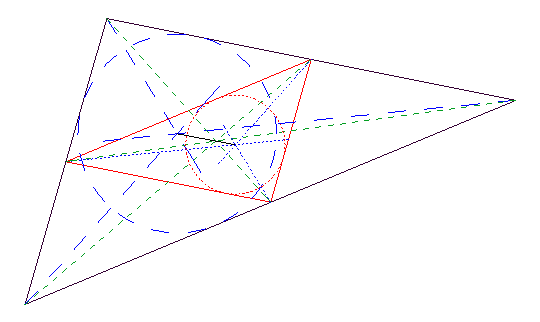
 Azt hiszem, az előző feladat után természetesen adódik, az érdeklődés miatt is, ha a térbeli analóg feladatot is kitűzöm.
67. feladat: Hol van a homogén vékony lemezből álló ABCD tetraéderhéj fizikai értelemben vett súlypontja.
|
|
|
|
|
|
|
| [372] jonas | 2006-02-23 22:45:46 |
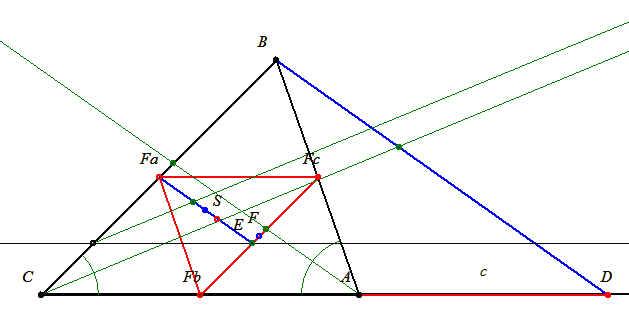
 Akkor a keresett pontot úgy is megkaphatjuk, hogy az eredeti háromszög beírt körének középpontját -1/2-szeresére nagyítjuk az eredeti háromszög súlypontjából, vagy úgy is, hogy az eredeti háromszög csúcsait b+c,c+a,a+b arányban súlyozzuk. (Hol is van az a háromszög-nevezetes-pont-katalógus?)
|
| Előzmény: [369] jonas, 2006-02-23 22:34:34 |
|
| [371] lorantfy | 2006-02-23 22:41:25 |
 Az FcEFa háromszög hasonló CDB háromszöghöz, így az Fc-ból induló szögfelező a szemközti oldalt éppen (b+c)/a arányban osztja. Tehát S pont az FaFbFc háromszög szögfelezőinek metszéspontja, vagyis a beírt körének középpontja.
|
 |
| Előzmény: [369] jonas, 2006-02-23 22:34:34 |
|
|
| [369] jonas | 2006-02-23 22:34:34 |
 Azzal hogy az egyes oldalakat drótból készítenénk el, egyenértékű, ha az oldalak felezőpontjába rakunk az oldalhosszal arányos súlyokat, és ezeknek a súlypontját keressük. Na de a középvonal-háromszög oldalai fele olyan hosszúak, mint az eredeti háromszög megfelelő oldalai. Ezért a középvonal-háromszög csúcsait kell súlyozni a szemközti oldalakkal, így pedig a beírt körét kapjuk.
|
| Előzmény: [368] jonas, 2006-02-23 22:29:56 |
|
|
| [367] jonas | 2006-02-23 22:26:52 |
 Nézzük csak. Nevezetes pont. Egy nagyon hosszú egyenlőszárú háromszögnek a felénél van, tehát nem lehet a magasságpont, a beírt kör középpontja, a súlypont vagy a Feuerbach kör középpontja, csak a körülírt kör középpontja lehetne. Az viszont nyilván nem lehet, mert az a háromszögön kívül is lehet, a drót súlypontja viszont nem. Akkor kevésbé nevezetes pont lesz.
|
| Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11 |
|
| [366] lorantfy | 2006-02-23 22:22:21 |
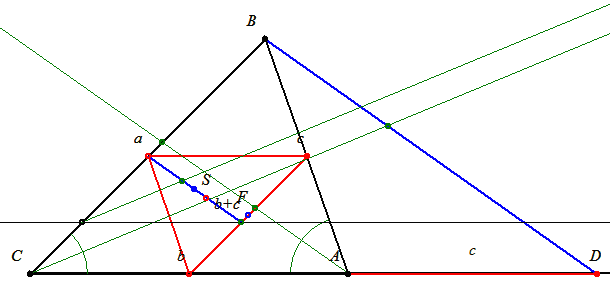
 Szerkesszük meg ezt a speciális súlypontot!
Az oldalfelező pontokba helyezzünk az oldalak hosszának megfelelő tömegpontokat.
A 'bc' szakaszt c/b arányban kell osztanunk. A szögfelező b/c arányban osztja. Tükrözzük ezt a pontot a szakasz felezőpontjára és helyezzünk ebbe a pontba b+c tömegpontot.
Már csak az 'a b+c' szakaszt kell (b+c)/a arányban felosztani. A C-ből induló szögfelező BD szakaszt a/(b+c). Ehhez hasonló kisháromszöget alakítunk ki és ebben a szögfelező azonos arányban osztja a szemközti oldalt.
Már csak tükröznünk kell ezt a pontot a felezőpontra. Ez lesz az S súlypont. Remélem idáig jó!
|
 |
| Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11 |
|
|
|
|
| [362] BohnerGéza | 2006-02-23 08:15:11 |
 66. feladat: Hol van egy homogén, vékony drótból készült ABC háromszögnek a fizikai értelemben vett súlypontja? ( ABC-hez kapcsolható nevezetes pont lesz.)
|
|




 szöggel jellemezve, mivel F rajta van OA Thalesz-körén
szöggel jellemezve, mivel F rajta van OA Thalesz-körén 


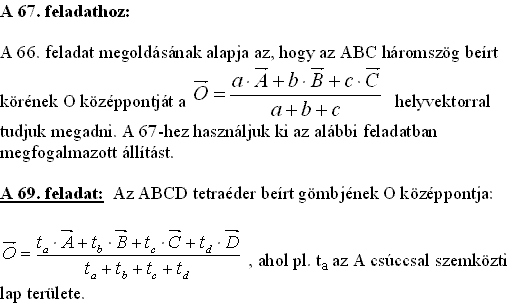







 -t és képezzünk egy nála kisebb hasonló
-t és képezzünk egy nála kisebb hasonló