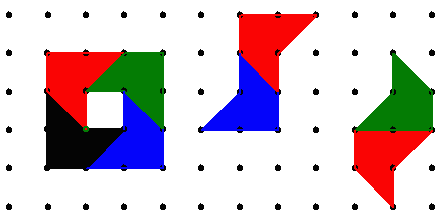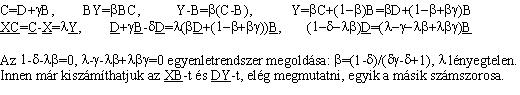|
| [79] lorantfy | 2004-02-29 22:31:52 |
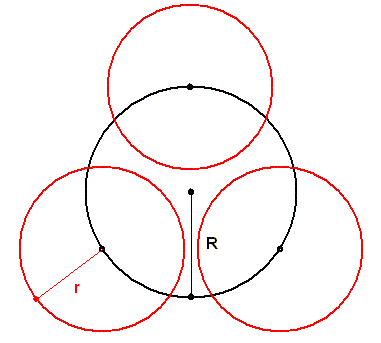
 18. feladat: Mekkor legyen r, hogy a piros körök negyedeljék a nagy kört? (Egyszerű, de nem akartam a "Grafi logikai" topikba tenni.)
|
 |
|
| [78] Sirpi | 2004-02-27 14:19:35 |
 Szia Miklós!
A feladat első részét bevállalom, azaz belátom, hogy nem-lyukas poliéderekre a szöghiány 720o.
Legyen a poliédernek c csúcsa, e éle és l lapja. Az Euler-féle poliéder-tétel szerint nemlyukas poliéderekre c-e+l=2.
Legyenek a poliéder lapjai rendre n1,n2,...,nl oldalúak. Ekkor 2e=n1+n2+...+nl, mert a lapok éleinek számát összeadva minden élt pontosan kétszer számolunk.
A szöghiány c.360o mínusz a poliéderlapok szögeinek összege. Definíció szerint ezt csúcsonként rendezve számoltuk ki, de megtehetjük ezt laponként rendezve is, a sorrend megváltoztatásával az összeg nem változik. Mivel egy ni oldalú lapon a szögösszeg (ni-2)180o, így a teljes szöghiány:
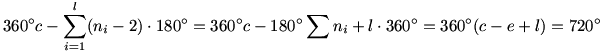
Látható, hogy az eredmény csak c-e+l értékétől függ, amit a test Euler-karakterisztikájának neveznek. "Egyszerű" testekre ez az érték 2, míg pl. tórusszal homeomorf alakzatokra ez az érték 0, ilyenkor a teljes (előjeles) szöghiány is 0o.
S
|
| Előzmény: [77] Kristóf Miklós, 2004-02-26 13:22:22 |
|
| [77] Kristóf Miklós | 2004-02-26 13:22:22 |
 Kedves Mindenki! Most egy kicsit nehéz feladat jön: Egy poliéder egy csúcsa körül valahány lap van, egy lapon a két él valamekkora szöget zár be. Adjuk össze a csúcs körül a szögeket, az eredmény egy konvex poliédernél kisebb mint 360 fok. Amennyivel kisebb, azt szöghiánynak nevezzük. Adjuk össze a poliéder összes csúcsának szöghiányát, egy gömbbel homeomorf poliéder esetén a teljes szöghiány 720 fok kell legyen. Példa: Kocka: 8 csúcs, egy csúcs körül 3x90 fok van, a szöghiány tehát 90 fok. 8 csúcs van, és 8x90 fok az 720 fok. Na, ennyit bevezetőnek. Egy síkbeli kirakómintánál a szöghiány nulla, ezért síkminta. Most jön a feladat: adjunk meg olyan alakzatot, amellyel a szöghiány nagyon pici de nem nulla, pl. kisebb mint 1 fok. Csináljunk ebből az alakzatból minél nagyobb lapszámú "gömböt"! Ez a kirakóminta lokálisan hasonlítson valamely síkbeli kirakómintára.
Ha ez a feladat így egyben túl komplikált, akkor egyszerűsíteni lehet. Lehet olyan minta is, ahol nem egy hanem 2 vagy 3 alakzat szerepel.
Például 3 féle rombuszból csináltam 132 oldalú "romboédert". Ha sikerül valahogy lefotóznom és beszkennelnem, akkor elküldöm a képét.
|
|
| [76] Kristóf Miklós | 2004-02-26 13:08:58 |
 Kedves Onogur! Valóban ezek a négyzet kirakások, azzal a kis kiegészítéssel, hogy az egyes gyűrűk helyettesíthetők a tükörképükkel is, így a 3x3-asra 2, az 5x5-ösre 4, a 7x7-esre 8, és általában 2 az n-iken különböző megoldás lehet.
Az extra elem nélküli téglalap lehetetlenségének bizonyítása majdnem olyan izgalmas, mint egy konkrét megoldás megtalálása!
|
| Előzmény: [71] Hajba Károly, 2004-02-24 12:57:06 |
|
| [75] Hajba Károly | 2004-02-25 23:42:25 |
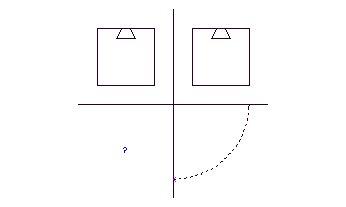
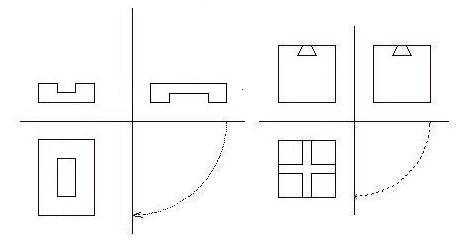
 17. feladat
Egy fakockába betétet véstünk az ábra szerint elől és oldalnézettel. Milyen lehet a felülnézete, ha tudjuk, hogy az egy darabból álló betét kivehető?
HK
|
 |
|
| [74] Hajba Károly | 2004-02-25 21:55:38 |
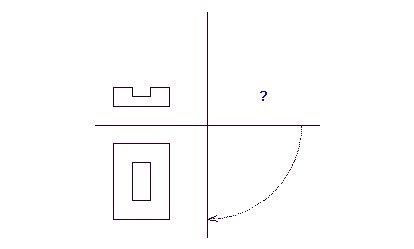
 16. feladat:
Egy kis "Ábrázoló geometria" - Milyen lehet az ábrázolt idom oldalnézete?
HK
|
 |
|
| [73] Csimby | 2004-02-25 10:43:41 |
 Szeretném kijavítani magamat, ugyanis 10 db. négyzetre mégiscsak találtam egy megoldást!
|
|
| [72] Csimby | 2004-02-24 20:52:49 |
 Kedves Onogur!
A feladatot először itt láttam: http://www.stetson.edu/ efriedma/touchingn/ , itt 4-re, 12-re és 14-re van megoldás, de a többi esetről semmmit sem mond. Én találtam megoldást minden páros n-re, azt pedig, hogy a páratlanok miért nem jók nagyon könnyű belátni. Az, hogy 6,8,10 -re miért nem jó szerintem nehezebb dió, tulajdonképpen csak 6-re néztem meg, mert nem találtam egyszerű módszert, de amit kitaláltam szerintem működik 8-ra és 10-re is. A feladatot egyébként úgy gondoltam, hogy összefüggő legyen az alakzat és a csúcsokban történő érintés is érintésnek számítson. Most lelőttem a poént, hogy mikor van megoldást, de a konstrukciókat és bizonyításokat attól még ki lehet találni, és elképzelhető, hogy 8,10-re van megoldás csak én nem találtam.
|
|
| [71] Hajba Károly | 2004-02-24 12:57:06 |
 Kedves Miklós!
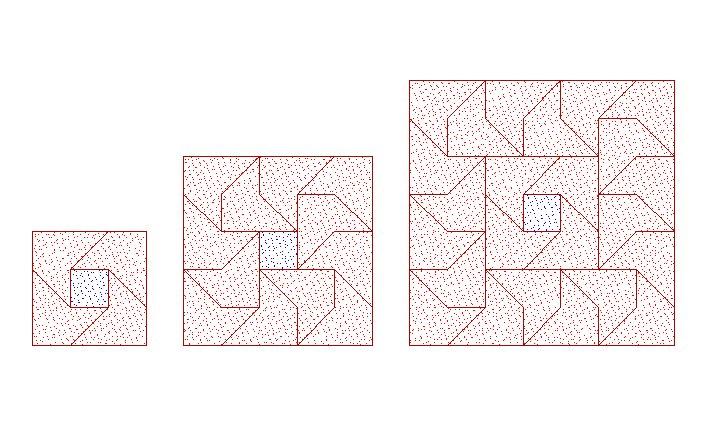
A 3*3, 5*5, 7*7, ... négyzet kirakása nagyságrendekkel könnyebb, mint az eredeti feladatod, főleg László képei után. Érdekes lenne a 4*4, ... 2n*2n, négyzeteket kirakni a kiegészítő négyzet számoságának bizonyos korlátozásával (,de ebbe még bele kellene mélyedni :o).
Szóval az az érzésem az eredeti feladattal kapcsolatban, hogy nagyobb valószínűséggel lehetne bizonyítani a kirakás lehetetlenségét, mint kirakni. De hát ez csak egy érzés.
S csak illusztrációnak az első bekezdésbeli kirakások:
|
 |
| Előzmény: [67] Kristóf Miklós, 2004-02-24 10:56:07 |
|
| [70] Hajba Károly | 2004-02-24 11:03:55 |
 Kedves Csimby!
Újabb érdekes feladatokat kotortál elő valahonnan.
Tehát, ha jól értem, akkor egységnégyzeteket kell lehelyeznünk.
Ha 4 db négyzetet úgy helyezek el, hogy az egy nagyobb négyzetet alkosson, akkor elvileg mind a 4 négyzet 3 másikat érint. Így elvileg minden n*4 négyzetet le lehet helyezni, hogy 3 másikat érintsen, feltéve, hogy nem egybefüggő alakzatot kell alkotni a végeredménynek.
Tehát a fenti hozzászólásomban 3 pontosítási eset is van:
(1) egységnégyzet; (2) "keresztbe érintés" sarok a sarokkal érintés-e; (3) a végeredmény lehet-e széteső vagy egybefüggőnek kell lennie?
HK
|
| Előzmény: [65] Csimby, 2004-02-23 23:17:38 |
|
| [69] Kristóf Miklós | 2004-02-24 11:03:10 |
 Kedves Lorantfi! Köszönöm az ábrát, igen, ez az az alakzat. Az első ábra prezentálja azt az esetet, amikor egy exta elemet, egy négyzetet is használok. Az eredeti feladatban viszont extra elem nélkül kell megcsinálni a téglalapot. Az alakzat tükörképe is használható. Úgy érzem, vagy nincs megoldás, vagy ha van akkor nagyon nagy.
|
| Előzmény: [60] lorantfy, 2004-02-18 13:46:01 |
|
|
| [67] Kristóf Miklós | 2004-02-24 10:56:07 |
 Kedves Géza! A feladat tőlem származik, nem emlékszem hogy valaha is láttam volna máshol. Természetesen fel lehet adni pontversenyben is, de azzal a megjegyzéssel hogy semmi se garantálja hogy létezik megoldás, illetve lehet hogy a legkisebb megoldás is többezer elemből áll. Én olyan versenyként adnám fel, ahol nem időre mérik a megoldást, hanem az nyer aki előbb beküld egy működő megoldást, és ezután még azok kapnak pontot akik ettől eltérő új megoldást küldenek be. A versenynél meg lehet említeni a nevem, hogy ez tőlem származik. Még nagyon sok feladatot tudok. Pl. feladat lehet aperiodikus de szabályos minták kirakása ezzel az alakzattal az egész síkon.További feladat lehet olyan kirakóminta, ahol ez az alakzat egy másikkal együtt szerepel párban. Pl. ha még egy egységnégyzet is megengedett, akkor lehet 3x3, 5x5, 7x7... stb négyzet kirakása. Milyen más extra alakzat jöhet szóba?
|
 |
| Előzmény: [63] Kós Géza, 2004-02-19 11:41:11 |
|
| [66] Csimby | 2004-02-23 23:23:30 |
 Bocsánat, kifelejtettem, hogy a négyzetek legyenek egybevágóak!
|
|
| [65] Csimby | 2004-02-23 23:17:38 |
 15.feladat El lehet-e helyezni 6,8,10 db. négyzetet a síkban úgy, hogy mindegyik pontosan 3 másikat érintsen?
El lehet-e helyezni páratlan sok négyzetet a síkban úgy, hogy mindegyik pontosan 3 másikat érintsen?
El lehet-e helyezni 4,12,14,16... db. négyzetet a síkban úgy, hogy mindegyik pontosan 3 másikat érintsen?
|
|
| [64] lorantfy | 2004-02-22 22:27:05 |
 Kedves Géza és Fórumosok!
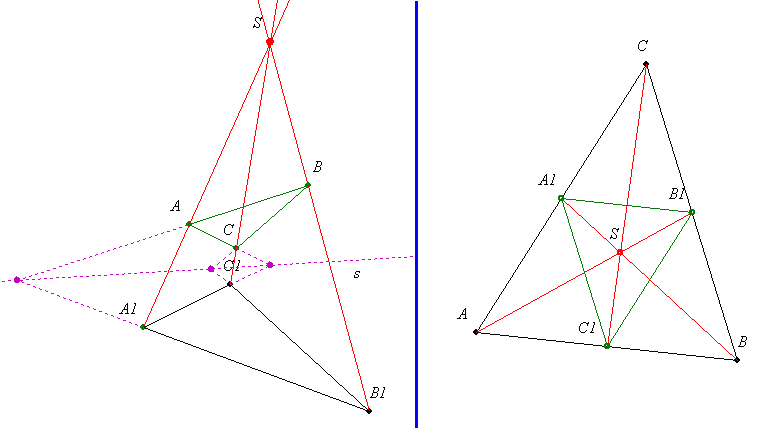
Desargues tétele: Ha két  csúcspontjait összekötő egyenesek: AA1, BB1 és CC1 egy S pontban metszik egymást, akkor a két csúcspontjait összekötő egyenesek: AA1, BB1 és CC1 egy S pontban metszik egymást, akkor a két  megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek. megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek.
A tétel megfordítása: Ha két  megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek, akkor a megfelelő csúcspontokat összekötő egyenesek: AA1, BB1 és CC1 egy pontban metszik egymást. megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek, akkor a megfelelő csúcspontokat összekötő egyenesek: AA1, BB1 és CC1 egy pontban metszik egymást.
Mi köze van a tétel megfordításásnak ahhoz, hogy a  súlyvonalai egy ponban metszik egymást? Az ábráról ez már leolvasható. súlyvonalai egy ponban metszik egymást? Az ábráról ez már leolvasható.
Ha a két  megfelelő oldalegyeneseinek metszéspontjai ideális pontok - vagyis ha az oldalegyenesek egymással párhuzamosak - a tétel akkor is igaz. A megfelelő oldalegyeneseinek metszéspontjai ideális pontok - vagyis ha az oldalegyenesek egymással párhuzamosak - a tétel akkor is igaz. A  középvonalai pedig nyilván párhuzamosak az oldalakkal. középvonalai pedig nyilván párhuzamosak az oldalakkal.
(A tétel a Hajós-ban: Ha két háromszög pontra nézve perspektív, akkor egyenesre nézve is perspektív és fordítva)
|
 |
| Előzmény: [58] Kós Géza, 2004-02-16 13:51:32 |
|
|
| [62] BohnerGéza | 2004-02-18 16:06:33 |
 Kedves Fórumosok!
Igazán nem László [56] és Géza [58] bosszantására ( sőt ha nem lesz más jelentkező, akkor az általuk várt megoldást is megadom), hanem tanulságos volta miatt írom a következőket:
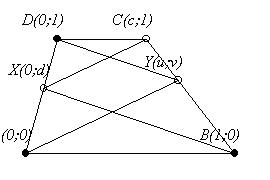
Amíg egyenesek párhuzamosságáról, metszéspontjukról van csak szó egy feladatban, célszerű lehet ferdeszögű koordinátarendszert használni. A krsz-t kezdőpontja és alapvektorai határozzák meg, melyekre ilyenkor elég, ha a nem párhuzamosak feltétel teljesül. A 14. feladat [46] esetén az A-t véve kezdőpontnak, az AB-t és AD-t véve alapvektornak a következő ábra alapján lehet számolni.
Ajánlom a módszert a 10.C. feladat [45] ábráját tekintve megoldására is. Ott célszerű a D-ből induló A ill. C felé mutató egységvektorokkal indulni. ( D(0;0), A(b;0), C(0;c), B(b;c), X(b;a), ... ) Igaz, így a megoldás annyira egyszerű lesz, hogy az már nem is szép, de a versenyen gyorsan, bemelegítésként megoldhatunk esetleg így egy feladatot.
|
 |
|
|
|
| [59] Kristóf Miklós | 2004-02-18 12:55:21 |
 Kedves Mindenki! Lehet-e téglalapot kirakni az alábbi alakzatból?
Bocs, nem tudom felrajzolni.Mindent egy sorba ír ez. Így kell rajzolni: Két lépés le, egy lépés jobbra, egy lépés jobbra fel, egy lépés balra, egy lépés balra fel. Ez tehát egy konkáv ötszög. A kirakást természetesen négyzethálós papíron kell elképzelni.
|
|
| [58] Kós Géza | 2004-02-16 13:51:32 |
 Csak egy apróság a projekítv geometria kedvelőinek.
Azt, hogy a súlyvonalak egy ponton mennek át, a Desargues-tétel megfordításával érdemes (és érdekes) kapcsolatba hozni. (Ezt is a feleségemtől tanultam. :-))
|
| Előzmény: [54] BohnerGéza, 2004-02-10 23:50:33 |
|
| [57] BohnerGéza | 2004-02-15 21:31:44 |
 Kedves László és Fórumosok!
László észrevétele teljesen jogos, nem egyszerű a javasolt megoldás, így további útmutatást adok. ( Nem gondoltam végig, ráadásul elszámoltam az Y vektort. )
A megoldás lényege a következő: A-ból B-be és D-be mutató vektorok és a gamma ismeretében a trapéz adott, a delta meghatározza X-et. Az AY párhuzamos XC feltétel meghatározza Y-t, tehát bétát is (deltától függ). Ehhez kihasználjuk majd, hogy ha pD=qB, akkor p=q=0, mivel d és B nem egyirányú vektorok. A béta ismeretében igazolható a BX párhuzamos YD. A megoldás befejezését most is az érdeklődőkre bízom. Jóval egyszerűbb a számolás, ha a helyvektorok kezdőpontjának a szárak metszéspontját vesszük, ezt is javaslom végigszámolni azoknak, akik még keveset foglalkoztak vektorokkal.
|
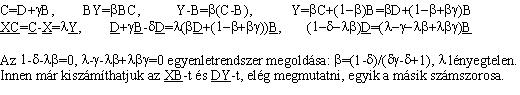 |
|
| [56] lorantfy | 2004-02-13 10:48:13 |
 Kedves Géza és Fórumosok!
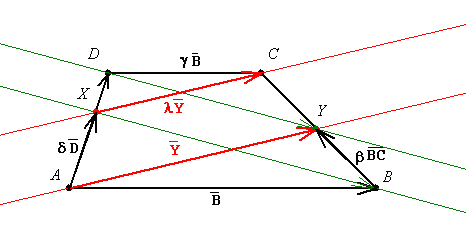
Természetesen bármilyen módszerrel adott megoldást szivesen látok a 14. feladatra. Azért szeretném ha megoldaná valaki a Papposz tétel felhasználásával is, hogy a [44] és [45] hozzászólásom ne legyen hiábavaló.
Persze Géza megoldási javaslatát is be kellene fejeznie valakinek...(Remélem Géza nem sértődsz meg érte, de szerintem a bafejezés nem mindenkinek nyilvánvaló!) Segítségül egy ábra:
|
 |
| Előzmény: [55] BohnerGéza, 2004-02-13 00:38:12 |
|












 csúcspontjait összekötő egyenesek: AA1, BB1 és CC1 egy S pontban metszik egymást, akkor a két
csúcspontjait összekötő egyenesek: AA1, BB1 és CC1 egy S pontban metszik egymást, akkor a két