|
| [964] BohnerGéza | 2007-12-31 14:05:01 |
 A megkötés valóban nem kell, a kitűzők talán a 9-eseknek szóló feladatot "nehezítették", lehessen általánosítani. A korosztálytól nem feltétlenül trigonometriát használó megoldást vártak. Az elemi tetszett nekem jobban.
|
| Előzmény: [963] SmallPotato, 2007-12-30 19:30:47 |
|
| [963] SmallPotato | 2007-12-30 19:30:47 |
 A megoldás szerintem is helyes. (Pontosabban: nekem is ez jött ki. :-) )
Két hozzáfűznivalóm lenne azért:
A feladat kifejezetten hegyesszögű háromszöget ír; Te nem ilyet rajzoltál, bár elsőre nekem sem tűnik lényeginek a megkötés. (Majd lehet, hogy engem is helyreigazítanak. :-D)
A másik: a jövőre nézve szerencsésebb lenne (mivel megszokott), ha a háromszög csúcsait az óramutató járásával ellentétes sorrendben betűznéd, és a szögeket ugyanezen sorrendben osztanád ki (az A csúcsban  , a B csúcsban , a B csúcsban  stb.) stb.)
Azért merem ezt kérni, mert emlékszem első táblai geometria-szereplésemre a gimiből: nem szokványosan betűztem a háromszöget, és a padsorokból tömény húúúúúú jött ... :-)))
|
| Előzmény: [962] S.Ákos, 2007-12-30 12:06:40 |
|
|
| [961] BohnerGéza | 2007-12-30 01:01:09 |
 A komáromi Selye János Magyar Tannyelvű Gimnázium Cornides István Emlékversenyének ( 2007.12.07 ) egy szép feladatát ajánlom:
128. feladat: Az ABC hegyesszögű háromszögben az A-nál lévő szög a B-nél lévő kétszerese. A C-ben a BC-re állított merőleges AB-t D-ben metszi. Mennyi az AC / BD arány?
|
|
|
| [959] Cogito | 2007-12-14 17:02:50 |
 Kedves HoA!
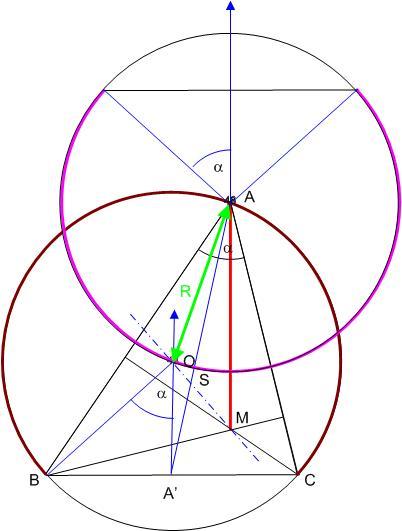
A feladatot pár napja én is megoldottam, csak az idő hiányzott, hogy letisztázva közölhető állapotba hozzam. Egyetértek azzal, hogy ez a kör a keresett mértani hely abban az esetben, ha a feladatot az ABC síkra szűkítjük. A részleteket most mellőzve nekem az jött ki, hogy a mértani helynek eleget tévő P pontokra teljesül, hogy
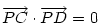 | (1) |
, ahol a C pontnak O-ra való középpontos tükörképe D. Mint látható, itt (egyrészt) azon pontok halmazáról van szó, melyekből a CD szakasz derékszög alatt látszik. Ez pedig az a C és D pontok nélküli gömbfelület, amely az Általad kapott kör CD körüli megforgatásával áll elő. Itt is igaz (másrészt) hogy a C és D pont is a mértani helyhez tartozik, hiszen a P C, vagy P C, vagy P D esetben egy-egy nullvektor miatt teljesül (1). A levezetés itt is megfordítható, tehát a teljes gömbfelület a keresett mértani hely. D esetben egy-egy nullvektor miatt teljesül (1). A levezetés itt is megfordítható, tehát a teljes gömbfelület a keresett mértani hely.
Ez az általános megoldás, hiszen a feladat szövege megengedi, hogy P-t térbeli pontnak tekintsük, a levezetés(ek) pedig ennek az értelmezésnek is eleget tesznek.
|
| Előzmény: [958] HoA, 2007-12-14 08:26:03 |
|
|
|
| [956] szegeddiák | 2007-11-28 21:32:57 |
 Sziasztok...segítségre lenne szükségem néhány feladatjoz..ha vki meg tudja oldani ezeket kérem rakja fel vagy vegye fel velem a kapcsolatot.Igazán sürgős lenne mert pénteken ebből zh-t írok.köszi előre is
tehát a feladatok: kocka élén áll ábrázolni Monge féle ábrázolással csúcsán álló , élén álló oktaéder ábrázolása monge féle ábrázolással teraéder lapján , csúcsán és élén áll szintén monge ábrázolással.
|
|
|
| [954] Hajba Károly | 2007-11-28 08:11:00 |
 Még mindig kevés az infó. A négyzet melyik egyenese az egyenes és melyik pontja a pont? Mikorra kellene? Péntekre tudnám elkészíteni a segédábrát, de majd az 'ábrázoló geometriában', oda való.
|
| Előzmény: [953] tyotyke, 2007-11-28 07:52:38 |
|
| [953] tyotyke | 2007-11-28 07:52:38 |
 Szia! Igen elhamarkodottan írtam le a dolgokat.Egy pont és egy egyenes két képéről van szó, és ebből kell egy kockát szerkesztenünk, csak a négyzetet azért irtam, mert az már 2-es és onnantól kezdve a magasságvonalak szerkesztésével a kocka csak néhány lépés. Fel kell vennünk egy első fővonalat......stb., leforgatotott háromszögből berajzoljuk a valódi kocka oldalhosszát.....Ezek lépések a szerkesztésből. Remélem igy már érthető!!!:) Köszönöm a segítséget,érdeklődést! Üdv!
|
|
| [952] HoA | 2007-11-27 18:47:11 |
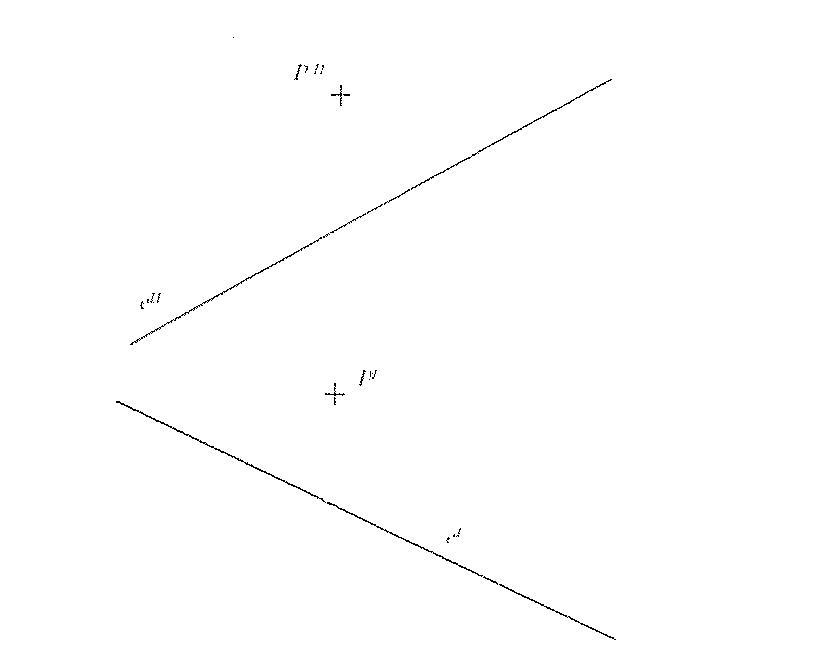
 Szia! Biztos vagy te abban, hogy ez két egyenes és két pont a síkban? Nem egy ábrázoló feladatról van szó és egy pont és egy egyenes két vetületét látjuk? ( Ehhez javasolnám az "ábrázoló geometria" témakört ). És mi a feladat? Hogy kell egy (vagy két?) pontból és egyenesből négyzetet és kockát szerkeszteni? Az ábrázoló esetben el tudok képzelni olyan feladatot, hogy szerkesszünk négyzetet, melynek egyik csúcsa az adott pont, oldalegyenese/átlóegyenese az adott egyenes. Vagy szerkesszünk kockát, melynek egyik csúcsa az adott pont, egyik élének/lapátlójának/testátlójának egyenese az adott egyenes. Ezek egyike a feladat?
|
| Előzmény: [950] tyotyke, 2007-11-27 12:18:55 |
|
|
| [950] tyotyke | 2007-11-27 12:18:55 |
 Sziasztok! Végig néztem a forum hozzászólásokat és meg kell hogy állapítsam, hogy itt profik társalognak! Ebből adódóan jött az ötletem, hogy a Ti segítségeteket fogom kérni és remélem segítetek is nekünk! Egy zh feladat megoldására lennénk kiváncsiak, szerkesztővonalak ábrázolásával és némi magyarázattal.A feladat általában egy tetszőlegesen adott két egyenes és két pont a síkban, amiből először egy négyzetet, majd abból egy kockát kell szerkeszteni. Megpróbálom a kiinduló ábrát csatolni, remélem sikerül. Segítségeteket előre is köszönöm!
|
|
|
|
| [947] BohnerGéza | 2007-11-26 13:20:09 |
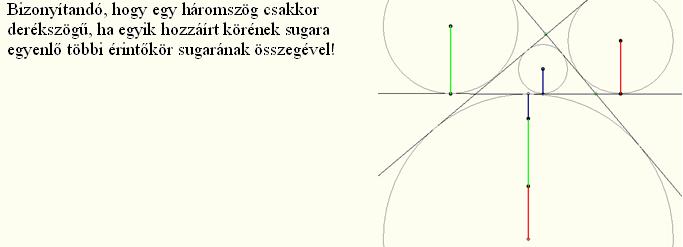
 A feladatot a következő érdekes észrevétel miatt tűztem ki:
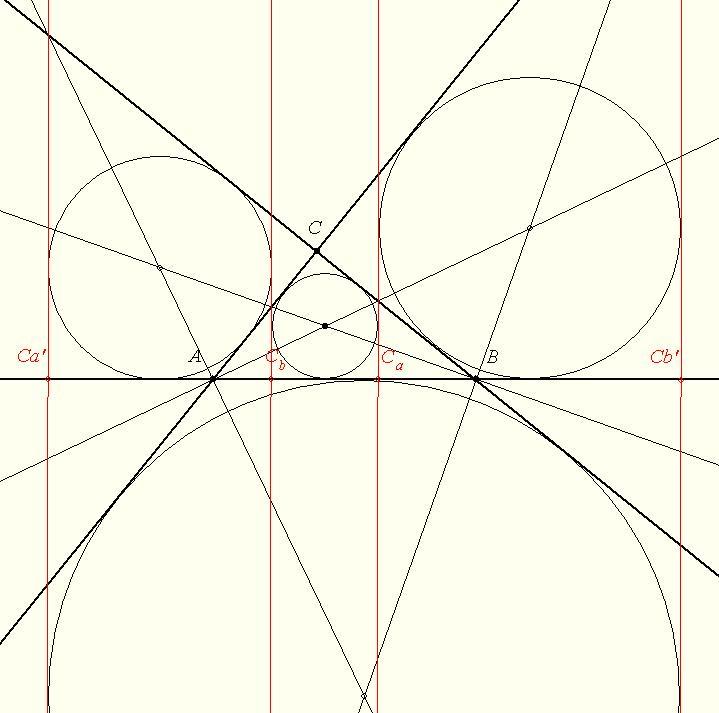
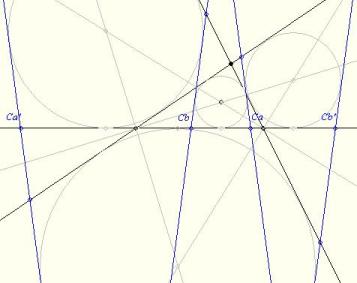
Legyen ABC C-nél derékszögű. Tükrözzünk a C-n nem átmenő szögfelezőkre! Például Ca' a C-nek az A-hoz tartozó külső szögfelezőre való tükörképe. Ekkor AC egyenes képe AB lesz és BC képe a Ca'-n átmenő AB-re merőleges egyenes, amely érint a b és c indexű hozzáírt köröket. ....
|
 |
| Előzmény: [946] HoA, 2007-11-26 10:29:32 |
|
|
| [945] Python | 2007-11-25 12:32:17 |
 Legyenek a háromszög oldalai a, b, c, beírt körésnek sugara r, a hozzáírt körök sugara ra, rb, rc (pl. ra az a oldalhoz írt kör) ! Tegyük fel hogy pl. rc=r+ra+rb! Felhasználva hogy a t háromszögterületre 2t=r(a+b+c)=ra(-a+b+c)=rb(a-b+c)=rc(a+b-c)
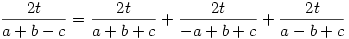
A nevezők a háromszög-egyenlőtlenség miatt pozitívak, felszorozva; 2t-vel osztva
![(a+b+c)\left[(a-b+c)(-a+b+c)+(a+b+c)(a-b+c+-a+b+c)\right]=](keplet.cgi?k=99215EE03C84BB72)
=(a+b+c)(a-b+c)(-a+b+c)
Elvégezve a műveleteket
4c(c2-b2-a2)=0
Itt 4c 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű. 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.
|
| Előzmény: [943] BohnerGéza, 2007-11-22 18:21:24 |
|
|
|
|
|



 =2
=2 , mivel a E a DCB háromszögben a körülírható kör kp-a. De így CDE
, mivel a E a DCB háromszögben a körülírható kör kp-a. De így CDE

 stb.)
stb.) 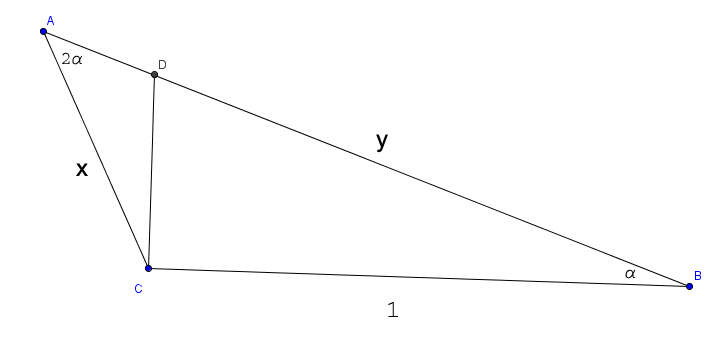


 C, vagy P
C, vagy P

 irányszögére - az MA = A'O iránytól mérve
irányszögére - az MA = A'O iránytól mérve  <
<


 =s-c;
=s-c;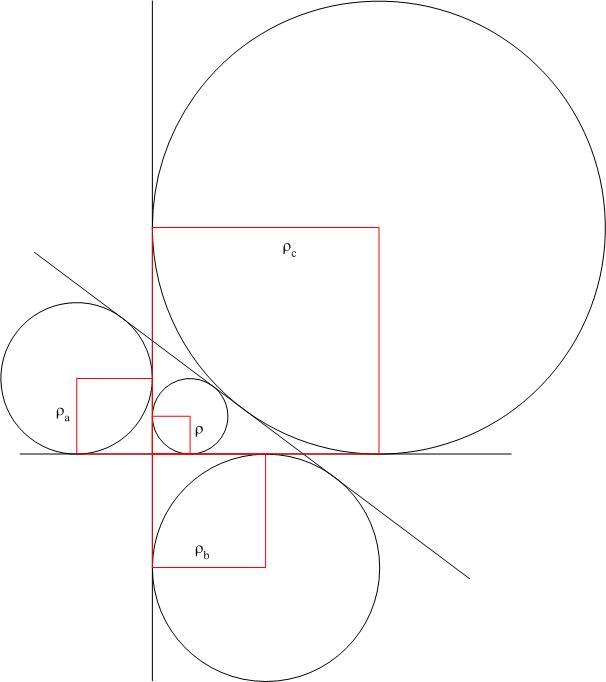

 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.
0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.