|
| [1949] Sinobi | 2022-01-20 17:35:41 |
 Szerintem ezt a kérdést megválaszoltam [1940]-ben, mekkorák az A és B-beli szögek.
A B-beli szög 64.34, az
A-beli szög 51.32.
Az ábrádat nem látom jól, de ha a 0 fok van jobb oldalt, és az alsó kör óramutatóval megegyezően, a felső pedig ellentétesen van számozva (???), akkor a metszéspontok az alsó körön
270 +- A-beli szög = 270 +- 51.32 = 321.32 és 218.68,
míg a felső körön
90 +- B-beli szög = 90 +- 64.34 = 154.34 és 25.66.
|
| Előzmény: [1947] HappyEffendi, 2022-01-19 20:34:48 |
|
| [1948] HappyEffendi | 2022-01-19 22:54:38 |
 Amint 1943-as hsz-ben jeleztem közreadnám a következő feladatot:
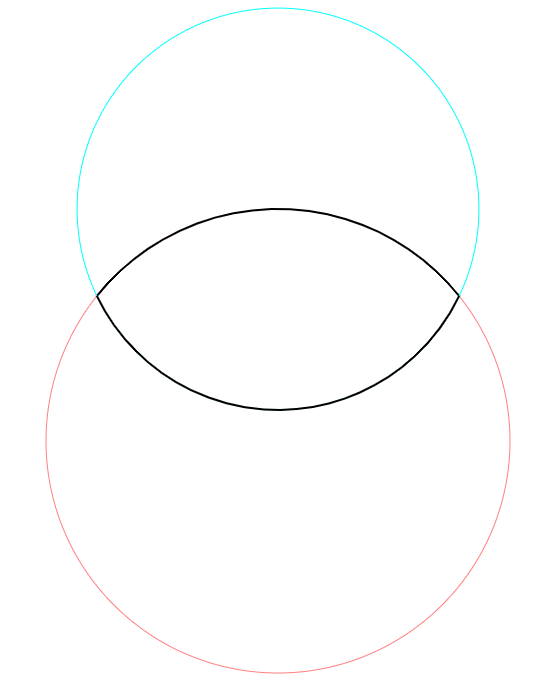
Adott egy 'r' sugarú kör, és annak ívén levő középponttal 6 db 'gyök(3)*r/2' sugarú kör.
Mekkora a 12 fehér köríves vonallal határolt alakzat területe?
|
 |
|
| [1947] HappyEffendi | 2022-01-19 20:34:48 |
 Kedves Erzsébet!
Köszönöm, hogy foglalkozol a témával!
Megpróbálom még szakszerűbben leírni a feladatot:
Adott két kör. A nagyobbik sugara 'r', a kisebbiké 'gyök(3)*r/2'. A kisebbik kör középpontja a nagyobbik 270. fokán van. 1943-as hozzászólás ábrája szerint.
A feladat: középpontjaiktól számítva egy-egy teljes körív mentén, hány foknál vannak a metszéspontjaik?
|
| Előzmény: [1946] Berko Erzsebet, 2022-01-17 16:58:15 |
|
| [1946] Berko Erzsebet | 2022-01-17 16:58:15 |
 Sajnos a pontos feladatot nem írtad. Adott két kör. Ha a metszéspontot összekötöm a körök középpontjával, akkor a szög: 64,34 fok. VAGY Két görbe hajlásszöge: metszéspontban húzott érintők által bezárt szög. Ez is 64,34 fok.
|
| Előzmény: [1945] HappyEffendi, 2022-01-16 23:46:29 |
|
|
|
| [1943] HappyEffendi | 2022-01-06 14:41:58 |
 Kedves Sinobi!
Boldog Újévet Kívánok (természetesen mindenki másnak is)!
Sejtettem, hogy szakszerűtlen lesz a feladat leírása, de a segítségeddel mégis sikerült elindulnom a megoldás felé, főleg, miután rájöttem, hol keressem az egyenlőszárú háromszöget. :)
Az alap kérdésem az lett volna, hogy egy-egy körnek hányadik fokainál vannak a másik körrel való metszéspontjai?
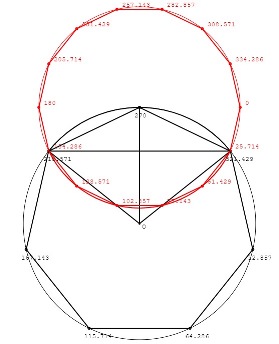
Szerkesztés közben arra is rájöttem, hogy a két kör metszéspontjai egy, a nagy körbe írható szabályos hétszög, és egy, a kis körbe írható szabályos tizennégy-szög egy-egy csúcsánál vannak.
Gondolom, a geometriában képzettek ezt kapásból tudtják.
A metszéspontok e szerint:
a kis körnél 25,714 és 154,286 fok,
a nagy körnél 218,571 és 321,429 fok,
az alábbi ábra szerint.
A fenti kérdés egy összetettebb feladat része volt, amivel, ha sikerül ábrázolnom, ismét jelentkezem.
Köszönöm segítségeteket!
|
 |
| Előzmény: [1941] Sinobi, 2021-12-31 10:11:02 |
|
| [1942] Berko Erzsebet | 2022-01-02 08:13:12 |
 Szerintem először le kellene írni a feladatot, vagyis pontosítani kellene. Metszéspontok szöge? Mivel ez számomra nem világos, én pl. a két érintő szögére gondoltam.
Két metsző kör szögén a metszéspontban meghúzott körérintők szögét értjük.
|
|
| [1941] Sinobi | 2021-12-31 10:11:02 |
 Mármint a szög arccos( (piros/2) / kék ), ahol a piros gyök(3)/2, a kék pedig 1.
|
|
| [1940] Sinobi | 2021-12-31 10:02:11 |
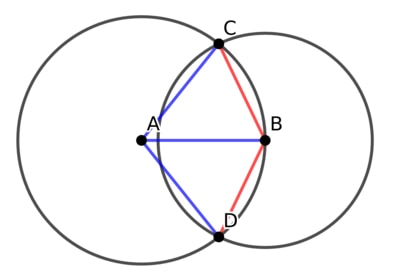
 Úgy értelmeztem a kérdésedet, hogy a körívek által bezárt szögre vagy kíváncsi (ábrán az ABC háromszög C-ben levő szöge). Most inkább úgy hiszem, hogy az ábrán az ABC háromszögben A-ban, illetve B-ben levő szögekre (vagy azok duplájára) vagy kíváncsi.
Akárhogy is, a háromszög oldalai (r, r, sqrt(3)/2 r), aminek az alapon fekvő szögei (C és B-beli szögek) arcos( kék/ (piros/2) ) = arccos( gyök(3) / 2 / 2), az A-beli szöge meg 180-2*arccos( gyök(3) / 4)).
|
 |
| Előzmény: [1939] HappyEffendi, 2021-12-30 20:31:56 |
|
|
| [1938] Sinobi | 2021-12-30 15:21:39 |
 Körök szöge az ugyanaz, mint a metszéspontba húzott sugarak szöge.
Ha felveszed a középpontokat és a metszéspontba húzott sugarakat, akkor egy (r,r,gyök(3)/2 r) egyenlőszárú háromszöget kapsz, és ennek a szögeire vagy kíváncsi.
|
| Előzmény: [1936] HappyEffendi, 2021-12-27 23:49:47 |
|
| [1937] HappyEffendi | 2021-12-28 00:14:23 |
 Elnézést, az ábra lemaradt, de talán nincs is rá szükség!
|
 |
|
| [1936] HappyEffendi | 2021-12-27 23:49:47 |
 Kedves Fórumozók!
Segítséget kérnék, mivel nem vagyok járatos a matematika és geometria világában:
Adott két egymást metsző kör. Az egyik r, a másik négyzetgyök(3) * r / 2 sugarú. A nagyobbik kör érinti a kisebbik középpontját.
Kérdésem: mi a képlet a metszéspontok szögeinek meghatározásához?
JavaScript-ben rajzoltam meg canvas-on, szemre többé-kevésbé jól kidekáztam az értékeket, de jó lenne, ha a gép pontosan kiszámolná. A teljesség kedvéért ideírom a körívrajzolás kódját:
ctx.arc(x, y, r, (Math.PI / 180) * 218.65, (Math.PI / 180) * 321.35);// nagy kör íve, ctx.arc(x, y, Math.sqrt(3) * r / 2, (Math.PI / 180) * 25.65, (Math.PI / 180) * 154.35);// kis kör íve, az óramutató járása szerint.
Bocsánat a valószínűleg szakszerűtlen feladatleírásért és előre is köszönök minden segítséget!
|
|
|
| [1934] Erben Péter | 2021-06-07 14:39:58 |
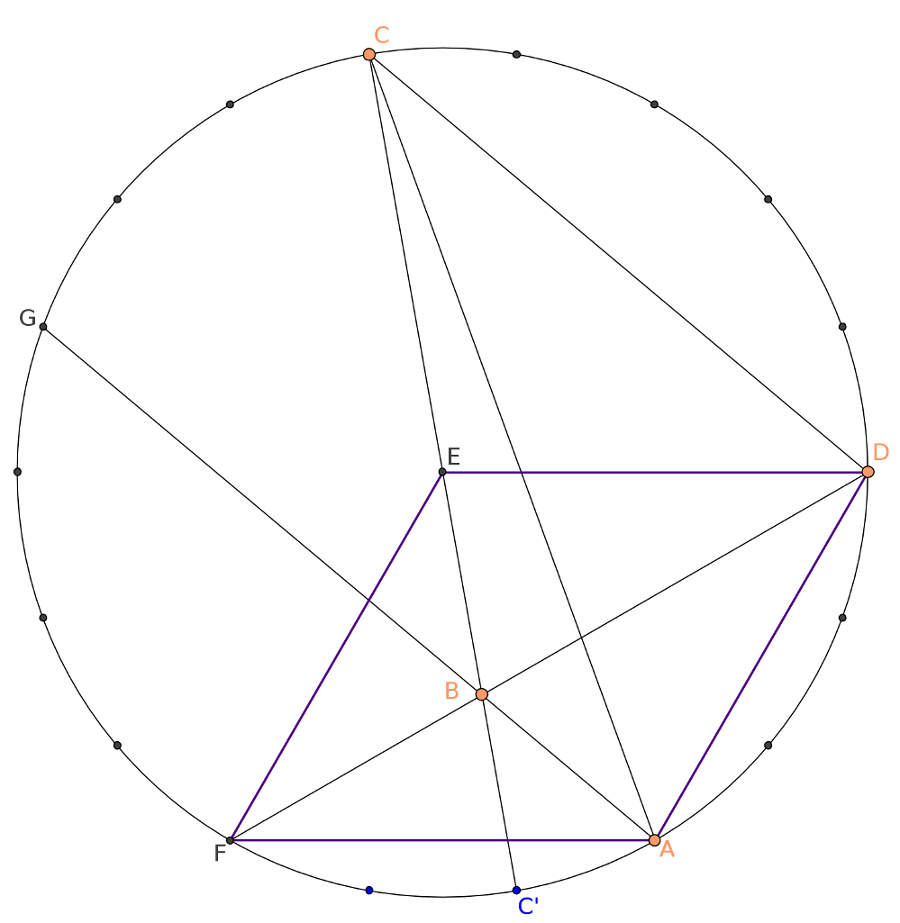
 A feladat egy lehetseges eredete a szabalyos 18-szog atloinak az a tulajdonsaga, hogy egymassal bezart szoguk mindig a 10 fok egesz tobbszorose.
Ha \(\displaystyle C\), \(\displaystyle D\) es \(\displaystyle A\) egy szabalyos 18-szog megfelelo csucsai, akkor \(\displaystyle E\) eppen a sokszog kozeppontja.
A kozbulso lepes, hogy a \(\displaystyle CC'\), \(\displaystyle AG\) es \(\displaystyle DF\) atlok egy ponton mennek at, ami peldaul visszavezetheto arra, hogy \(\displaystyle EDAF\) egy rombusz, amelynek szogei 120 fok es 60 fok.
Mindez persze nem a feladat megoldasa, inkabb azt mutatja, hogyan "keszulhetett" a kerdes.
|
 |
| Előzmény: [1933] Lpont, 2021-06-07 12:32:53 |
|
| [1933] Lpont | 2021-06-07 12:32:53 |
 I. Szögszámolással adódik, hogy BD felezi az ABCD négyszög B-nél levő szögét.
II. A-t tükrözve BD-re a kapott E pont rajta van BC egyenesén és AD=ED.
III. Újabb szögszámolás után EDC háromszög egyenlő szárú, ED=EC.
IV. Harmadjára is szögeket számolva EC=EA, tehát AE=EC=ED=AD, azaz AED háromszög szabályos, minden szöge 6alfa, így alfa=10fok.
|
| Előzmény: [1932] rezes, 2021-06-06 13:18:23 |
|
| [1932] rezes | 2021-06-06 13:18:23 |
 \(\displaystyle ABCD\) konvex négyszögben \(\displaystyle BC=CD, BAC\sphericalangle=3\alpha\), \(\displaystyle BCA\sphericalangle=\alpha,\) \(\displaystyle ACD\sphericalangle=3\alpha\), \(\displaystyle DAC\sphericalangle=5\alpha.\) Mennyi \(\displaystyle \alpha\) értéke?
|
|
| [1931] HoA | 2021-02-03 12:52:03 |
 Bocsánat, elírás. Helyesen:
A \(\displaystyle D_0D_1F_1\) és \(\displaystyle D_0D_2F_2\) háromszögek hasonlók, \(\displaystyle D_0, F_1 és F_2\) egy egyenesen vannak.
|
| Előzmény: [1930] HoA, 2021-02-03 12:34:31 |
|
| [1930] HoA | 2021-02-03 12:34:31 |
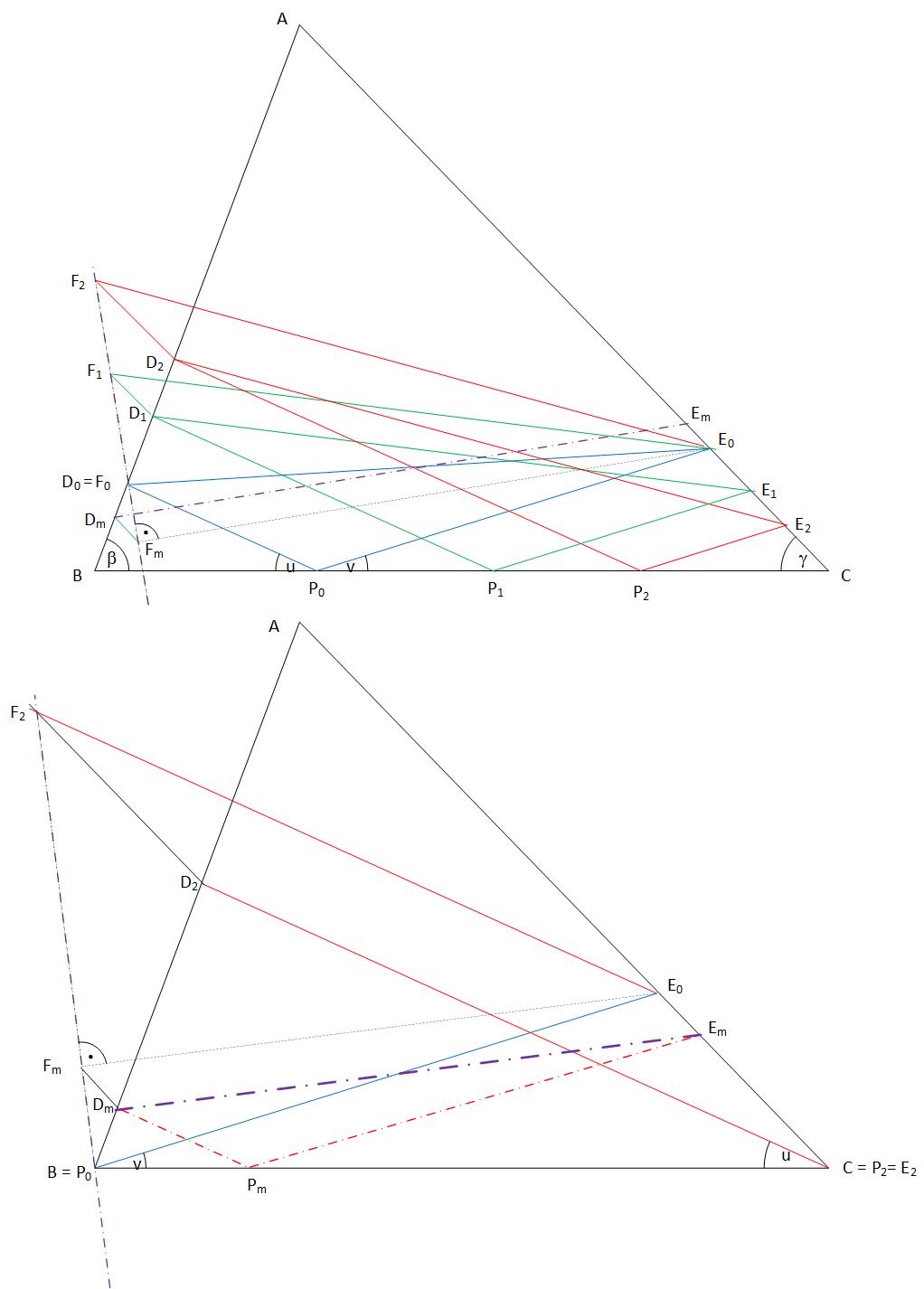
 Legyen \(\displaystyle P\) egyik helyzete \(\displaystyle P_0\). Rajzoljuk meg az ehhez tartozó \(\displaystyle P_0D_0\) és \(\displaystyle P_0E_0\) szakaszokat. P egy másik, \(\displaystyle P_1\) helyzetéhez tartozzanak A \(\displaystyle D_1\) és \(\displaystyle E_1\) pontok. A párhuzamos szelők tétele szerint \(\displaystyle BP_0 D_0\) háromszögből \(\displaystyle D_0D_1 = k P_0P_1\) , ahol \(\displaystyle k = \frac{sin u}{sin(\beta + u)}\) . Hasonlóan a \(\displaystyle P_0CE_0\) háromszögből \(\displaystyle E_0E_1 = m P_0P_1\) , ahol \(\displaystyle m = \frac{sin v}{sin(\gamma + v)}\) . Toljuk el \(\displaystyle E_1D_1\) -et önmagával párhuzamosan az \(\displaystyle AC\) egyenes mentén úgy, hogy \(\displaystyle E_1\) \(\displaystyle E_0\) -ba kerüljön. \(\displaystyle D_1\) új helyzete legyen \(\displaystyle F_1\) . \(\displaystyle D_1E_1E_0F_1\) paralelogramma, \(\displaystyle D_1F_1 \# E_1E_0\) , \(\displaystyle \frac{D_0D_1}{D_1F_1} = \frac {k}{m}\). Ismételjük meg egy további \(\displaystyle P_2\) pontra a \(\displaystyle P_1\) -re elvégzetteket. Kapjuk a \(\displaystyle D_2 , E_2, F_2\) pontokat. \(\displaystyle \frac{D_0D_2}{D_2F_2} = \frac {k}{m}\). A \(\displaystyle D_0D_1F_1\) és \(\displaystyle D_0D_2F_2\) háromszögek hasonlók, \(\displaystyle D_0, D_1 és D_2\) egy egyenesen vannak. A megfelelő \(\displaystyle D_iE_i\) szakasszal párhuzamos és azonos hosszúságú \(\displaystyle F_iE_0\) szakaszok egyik végpontja közös (\(\displaystyle E_0\)) , a másik az \(\displaystyle F_iF_j\) egyenesen mozog. Közülük a legrövidebb az \(\displaystyle E_0\) -ból az \(\displaystyle F_iF_j\) -re bocsátott merőleges \(\displaystyle F_m\) talppontját \(\displaystyle E_0\) -lal összekötő szaksz lesz. A keresett legrövidebb \(\displaystyle DE\) szakaszt akkor kapjuk, ha \(\displaystyle E_0F_m\) -et az \(\displaystyle AC\) egyenes mentén úgy toljuk el, hogy \(\displaystyle F_m\) az \(\displaystyle AB\) egyenesre essék, a szakasz végpontjai legyenek \(\displaystyle D_m és E_m\)
A szerkesztést úgy hajthatjuk végre a legkevesebb vonal megrajzolásával, ha P két szélső helyzetét használjuk. Legyen tehát \(\displaystyle P_0 = B, P_2=C\) , \(\displaystyle E_0\) az \(\displaystyle AC\) oldalnak az a pontja, melyre \(\displaystyle E_0BC \angle = v\) , \(\displaystyle D_2\) az \(\displaystyle AB\) oldalnak az a pontja, melyre \(\displaystyle D_2CB \angle =u\) . \(\displaystyle CD_2\) -t \(\displaystyle CA\) mentén úgy eltolva, hogy \(\displaystyle C\) \(\displaystyle E_0\) -ba jusson \(\displaystyle D_2\) kerüljün \(\displaystyle F_2\) -be .\(\displaystyle E_0\) -ból az \(\displaystyle F_2B\) egyenesre bocsátott merőleges talppontja legyen \(\displaystyle F_m\) . A legrövidebb DE szakaszt \(\displaystyle E_0F_m\) -nek \(\displaystyle AC\) -vel párhuzamos eltolásával kapjuk úgy, hogy \(\displaystyle F_m\) az \(\displaystyle AB\) egyenesen lévő \(\displaystyle D_m\) -be kerüljön, \(\displaystyle E_0\) pedig \(\displaystyle E_m\) -be.
Ujjgyakorlatnak hagyjuk annak bizonyítását, hogy a \(\displaystyle D_m\) -ből \(\displaystyle D_2C\) -vel húzott párhuzamos és az \(\displaystyle E_m\) -ből \(\displaystyle E_0B\) vel húzott párhuzamos egy, a \(\displaystyle BC\) egyenesen fekvő, feladatunk megoldását adó \(\displaystyle P_m\) pontban metszik egymást.
|
 |
| Előzmény: [1929] sakkmath, 2021-01-21 23:58:57 |
|
| [1929] sakkmath | 2021-01-21 23:58:57 |
 A 192. feladat valóban nyitott. Talán ezért (is) nagyon nehéz, de megoldható. Az általam ismert megoldást nyolc éve publikálták, azóta a közlés helyén, egy közismert, frekventált oldalon, állócsillagként ragyog: még nem reagált rá senki – legalábbis ott nem. Ebből arra következtetek, hogy máig csak ez az egy megoldás létezik. Ez a dolgozat – a szerkesztéses részét tekintve – mindvégig euklideszi szerkesztésekkel jut el a \(\displaystyle P\) pont keresett pozíciójához.
Beírom a lényegesen könnyebb,193. feladatot is, amely csak u és v szerepét tekintve különbözik a rokon 192.-től. Találjunk euklideszi szerkesztést alkalmazó megoldást a következő, 193. feladatra:
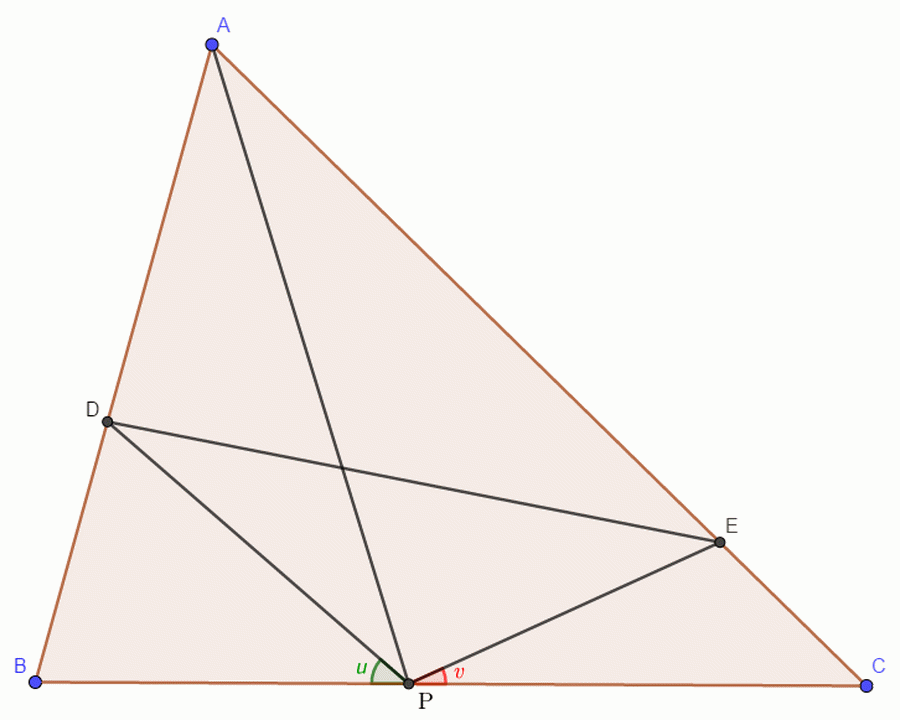
Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalán mozog egy \(\displaystyle P\) pont. Az \(\displaystyle AB\) oldal \(\displaystyle D\), valamint az \(\displaystyle AC\) oldal \(\displaystyle E\) pontjára fennáll, hogy rögzített e két szög: \(\displaystyle u=BPD∠\) és \(\displaystyle v=CPE∠\). Keressük meg a \(\displaystyle P\) pont azon helyzetét, amelyre a \(\displaystyle DE\) szakasz hossza minimális!
|
 |
| Előzmény: [1928] Sinobi, 2021-01-19 18:24:05 |
|
| [1928] Sinobi | 2021-01-19 18:24:05 |
 Nagyon nyitott a feladat, és nekem kételyeim is vannak azzal kapcsolatban, hogy van értelmes, szép válasz. Az ennél egyszerűbbnek tűnő
Philo szelő probléma: adott egy szög és benne egy pont, keressük meg a legrövidebb szakaszt, amely átmegy a ponton, és a végpontjai a szög két szárán van
sem szerkeszthető már körzővel és vonalzóval. Bár az például megoldható olyan eszközzel, amelyik megadja két kúpszelet metszéspontjait.
|
|
| [1927] sakkmath | 2021-01-13 23:43:55 |
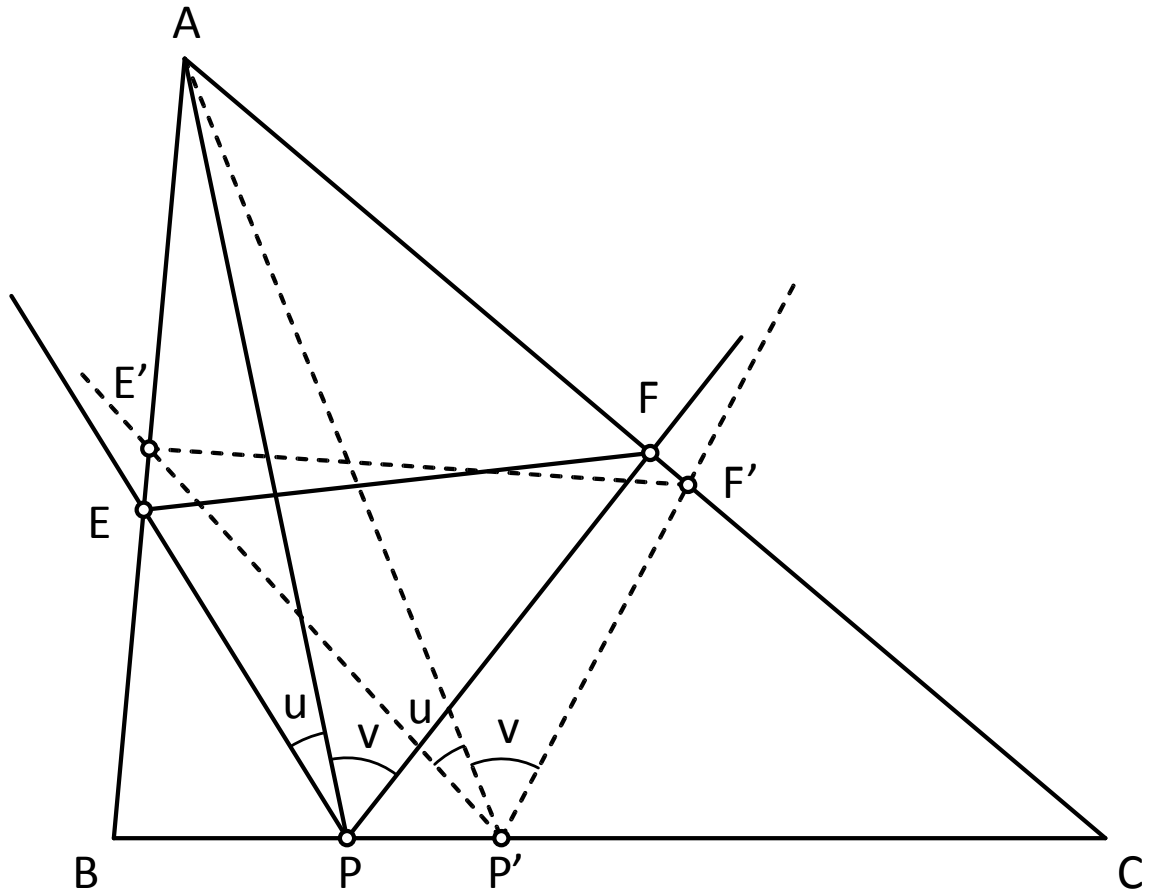
 \(\displaystyle {\bf 192.}\) \(\displaystyle {\bf feladat}\): Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalán mozog egy \(\displaystyle P\) pont. Az \(\displaystyle AB\) oldal \(\displaystyle E\), valamint az \(\displaystyle AC\) oldal \(\displaystyle F\) pontjára fennáll, hogy konstans az \(\displaystyle u = EPA\angle\) és a \(\displaystyle v = APF\angle\). Keressük meg a \(\displaystyle P\) pont azon helyzetét, amelyre az \(\displaystyle EF\) szakasz hossza minimális!
|
 |
|
| [1926] HoA | 2019-12-06 14:58:36 |
 Mit nevezzünk helytállónak? A módszer körívekből állít össze egy, az ellipszist közelítő görbét. Megvizsgálhatjuk például, a megfelelő tengelyeket egymásra fektetve a tengelyek hosszának függvényében a nagytengely pontjait abszcisszáknak, az ellipszis ill. a közelítő görbe hozzárendelt pontjait ordinátáknak tekintve, mennyi az ordináták eltérésének maximuma. Vagy mekkora a két görbe közötti területdarabok "vastagsága" . Te mire gondoltál ?
|
| Előzmény: [1925] TTibi, 2019-12-04 16:55:34 |
|














