A 33. Nemzetközi Fizikai Diákolimpiai feladatai

A feladatok megoldását novemberi számunkban közöljük.

Elméleti forduló

A feladatok kidolgozására 5 óra állt a versenyzők rendelkezésére.

1. feladat. Földbe hatoló radar

A földbe hatoló radart a földfelszín alatt, nem túl mélyen elhelyezkedő tárgyak felderítésére és helyük meghatározására használják. Működésének lényege, hogy elektromágneses hullámokat sugároz a földbe, és érzékeli a tárgyakról visszaverődő hullámokat. Az antenna és az érzékelő közvetlenül a föld felszínén, ugyanabban a pontban helyezkedik el.

Ha egy \(\displaystyle \omega\) körfrekvenciájú, lineárisan polarizált elektromágneses síkhullám a z tengely irányában halad, akkor benne az elektromos térerősség a következő összefüggéssel írható le:

(1)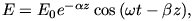

ahol E₀ állandó, a csillapodási együttható, \(\displaystyle \beta\) pedig a (kör)hullámszám. Esetünkben \(\displaystyle \alpha\) és a következő összefüggésekkel adható meg:

(2)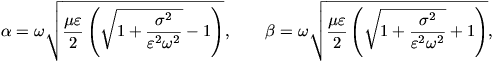

ahol \(\displaystyle \mu\), \(\displaystyle \varepsilon\) és \(\displaystyle \sigma\) a közeg mágneses permeabilitását, elektromos permittivitását és elektromos vezetőképességét jelöli. (=_0r, =\(\displaystyle \varepsilon\)_0r, a vezetőképesség pedig a fajlagos ellenállás reciproka.)

Egy, a talajban lévő tárgyat érzékelhetetlennek tekintünk, ha a felszínről induló radarjel amplitúdója 1/e-nél (37%-nál) nagyobb arányban csökken le akkorra, amikor a jel a tárgyhoz érkezik. Rendszerint 10 MHz-1000 MHz között változtatható frekvenciájú elektromágneses hullámot használnak, mert ez felel meg a tárgyak helymeghatározásának és az észlelés felbontóképességének.

A radar felhasználhatósága függ a felbontóképességétől. A felbontóképesség az a minimális távolság, amely esetén még két ilyen közeli visszaverő objektum megkülönböztethető. Ez határesetben azt jelenti, hogy a két objektumról visszaverődő hullám fáziskülönbsége a detektornál (alkalmas helyzetben) eléri a 180^o-ot.

(Adatok: \(\displaystyle \mu\)₀ =4\(\displaystyle \pi\)^.10^-7 H/m és ₀=8,85^.10^-12 F/m.)

Kérdések

1. Tételezzük fel, hogy a talaj nem mágneses (=₀), és teljesül, hogy \(\displaystyle \left(\frac{\sigma}{\omega\varepsilon}\right)^2\ll1\). Az (1) és (2) összefüggések felhasználásával add meg a hullám v terjedési sebességét \(\displaystyle \mu\)-vel és \(\displaystyle \varepsilon\)-nal kifejezve (1,0 pont).

2. Határozd meg a talajbeli érzékelés maximális mélységét, ha a talaj vezetőképessége 1,0 mS/m, permittivitása 9\(\displaystyle \varepsilon\)₀, valamint teljesül a 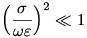feltétel! (S = ohm^-1, és felhasználhatod, hogy =₀.) (2,0 pont).

3. Tegyük fel, hogy két párhuzamos vezető rúd fekszik a talajban 4 méter mélyen. A talaj vezetőképessége 1,0 mS/m, és a permittivitása 9\(\displaystyle \varepsilon\)₀. A radar jó közelítéssel az egyik rúd felett van. Tételezzük fel, hogy az érzékelő pontszerű. Határozd meg, hogy legalább mekkora frekvenciára van szükség ebben az elrendezésben 50 cm-es vízszintes (oldalirányú) felbontóképesség eléréséhez (3,5 pont)!

4. Ugyanebben a talajban meg szeretnénk mérni, hogy egy vízszintesen eltemetett rúd mekkora d mélységben fekszik. Ezért a detektorral, a talajon, a rúdra merőleges irányban fekvő x egyenes mentén méréseket végzünk, mérjük egy radarimpulzus visszaérkezésének t idejét. Az eredményt az 1. ábra mutatja.

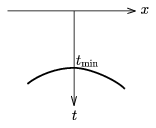
1. ábra. A t visszaérkezési idő az x detektorhelyzet függvényében, t_min  = 100 ns

Add meg a t visszaérkezési időt x függvényeként, és határozd meg a d mélységet (3,5 pont)!

2. feladat. Elektromos jelek érzékelése

Néhány tengeri állat képes bizonyos távolságból más élőlényeket érzékelni olymódon, hogy ezek az élőlények (például légzésük közben, vagy más izomösszehúzódással járó folyamat során) elektromos áramokat hoznak létre. Vannak olyan ragadozók, melyek ezt az elektromos jelet használják fel arra, hogy meghatározzák zsákmányuk helyzetét, még akkor is, ha az homokkal van betemetve.

A zsákmányállat által keltett áram és a ragadozó észlelési folyamatának fizikai mechanizmusát az 2. ábrán látható módon modellezhetjük. A zsákmány által keltett áram két gömb között folyik, melyek a zsákmány testében találhatóak, és egyik pozitív, másik negatív potenciálú. A két gömb középpontja közti távolság l_zs, mindkét gömb sugara r_zs, ami sokkal kisebb, mint l_zs. A tengervíz fajlagos ellenállása . Tételezzük fel, hogy a zsákmányállat testének fajlagos ellenállása ugyanakkora, mint a környező tengervízé.

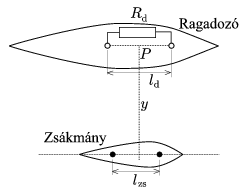
2. ábra. Egy modell, ami bemutatja, hogyan érzékeli egy ragadozó a zsákmányból származó elektromos teljesítményt

Annak érdekében, hogy leírjuk, hogyan érzékeli a zsákmányból származó elektromos teljesítményt a ragadozó, az előzőekhez hasonlóan az érzékelőt (detektort) is két gömbnek tekintjük, melyek a ragadozó testében helyezkednek el, érintkeznek a környező tengervízzel, és párhuzamosan fekszenek a zsákmány testében lévő gömbpárral. Ezek a gömbök l_d távolságra helyezkednek el egymástól, mindkettőjük sugara r_d, ami sokkal kisebb, mint l_d. Esetünkben az észlelő középpontja y távolságra helyezkedik el a zsákmánytól, és éppen a forrás felett található. Mind l_zs, mind l_d sokkal kisebb, mint y. Az elektromos térerősség a ragadozó helyén, a két gömböt összekötő vonal mentén állandónak tekinthető. Ennek megfelelően feltehetjük, hogy az észlelő, amely a zsákmányhoz, a környező tengervízhez és a ragadozóhoz csatlakozik, a 3. ábrán bemutatott módon zárt áramköri rendszert alkot.

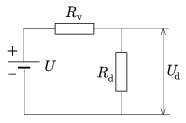
3. ábra. Az érzékelő ragadozót, a zsákmányt, és a környező tengervizet magában foglaló ekvivalens zárt áramköri rendszer

Az ábrán feltüntetett U potenciálkülönbség a zsákmány által a ragadozó leendő helyén keltett elektromos mezőben az érzékelő gömbök középpontjai között fellépő feszültséggel egyenlő (amikor a ragadozó még nincs is a helyén). R_v a környező tengervíz ellenállása, R_d a ragadozó érzékelő (detektáló) egységének ellenállása, U_d pedig a detektáló gömbök közötti feszültség az észlelés közben.

Kérdések

1. Tekintsünk egy végtelen, homogén közegben levő pontszerű áramforrást, amiből I áram folyik ki. Határozd meg a j áramsűrűség vektort (egységnyi felületen átmenő áramot) a forrástól r távolságban (1,5 pont)!

2. Az E=^.j differenciális Ohm-törvényre alapozva határozd meg az E_r elektromos térerősség vektort a ragadozó állat érzékelő gömbjei közötti P pontban (lásd a 2. ábrát) egy olyan esetben, amikor a zsákmány testében lévő gömbök között I_zs áram folyik (2 pont).

3. Ugyanezen I_zs áramra határozd meg a zsákmányban lévő forrásgömbök közötti U_zs feszültséget (1,5 pont)!

Határozd meg a két forrásgömb közötti R_zs ellenállást és a forrás P_zs teljesítményét (1 pont)!

4. Határozd meg a 3. ábrán lévő R_v és U_d értékeket (1,5 pont), és számítsd ki a forrásból a detektorba átvitt P_d teljesítmény értékét (0,5 pont)!

5. Határozd meg R_d optimális értékét, amely az észlelt teljesítmény maximumához vezet (1,5 pont), és határozd meg a maximális teljesítmény nagyságát is (0,5 pont)!

3. feladat. Lejtős úton mozgó nehéz jármű

A 4. ábra egy nehéz jármű (például egy pótkocsi) egyszerűsített modelljét mutatja. A jármű hajlásszögű lejtős úton halad, első és hátsó kerekei hengerszimmetrikusak. Mindkét kerék M tömegű, vastag, hengeres csőnek tekinthető, melyek külső sugara R₀, míg belső sugaruk R_i = 0,8 R₀, továbbá a kerekeknek küllőik is vannak, egy-egy keréken 8 darab, a 8 küllő teljes tömege 0,2 M. A kerekek az 5. ábrán látható módon modellezhetők. A járműtestet tartó alvázszerkezet tömege elhanyagolható. A jármű az úton lefelé halad, mozgását a nehézségi és a súrlódási erők határozzák meg. Az első és a hátsó kerék a járműhöz képest szimmetrikusan helyezkedik el.

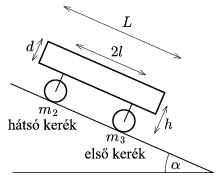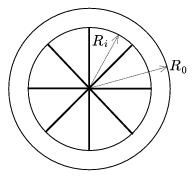4. ábra	5. ábra. A kerekek egyszerűsített modellje

A henger és az út közötti tapadási (statikus), illetve csúszási (kinetikus) súrlódási együtthatókat jelöljük rendre \(\displaystyle \mu\)_s-sel és \(\displaystyle \mu\)_k-val. A téglatest alakú járműtest tömege m₁ = 5 M, hossza L, vastagsága pedig d. Az első és a hátsó kerekek tengelyei közötti távolság 2 l, míg a kerekek középpontjának a járműtest középsíkjától mért távolsága h. Tételezd fel, hogy a kerekek súrlódásmentesen csapágyazottak.

Kérdések

1. Számítsd ki az egyes kerekek tehetetlenségi nyomatékát (1,5 pont)!

2. Rajzold le a járműtestre, továbbá az első és a hátsó kerekekre ható összes erőt! Minden egyes részre írd fel a mozgásegyenleteket (2,5 pont)!

3. A jármű nyugalomból indul, és a nehézségi erő hatására szabadon mozog. Állapítsd meg a rendszer összes lehetséges mozgástípusát, és határozd meg az egyes gyorsulásokat a megadott fizikai mennyiségek segítségével (4 pont)!

4. Tegyük fel, hogy a jármű nyugalomból indulva tiszta gördüléssel éppen d utat tett meg, amikor az útnak egy olyan szakaszára érkezik, ahol a súrlódási együtthatók hirtelen kicsiny \(\displaystyle \mu\)_s' és \(\displaystyle \mu\)_k' értékekre csökkennek, és így mindkét kerék csúszni kezd.

Számítsd ki az egyes kerekek haladási sebességét és szögsebességét, amikor a jármű a nyugalmi helyzethez képest összesen s méter utat tett meg. Ekkor feltehetjük, hogy d és s sokkal nagyobbak, mint a jármű méretei (2 pont).

Kísérleti forduló

A feladatok kidolgozására összesen 5 óra állt a versenyzők rendelkezésére.

I. feladat. Az e/k_B arány meghatározása elektrolízissel

Elméleti áttekintés

A víz elektrolízisét a következő reakcióval írhatjuk le:

\(\displaystyle \rm H_2O\to2\,H^++O^{2-},\)

\(\displaystyle \rm2\,H^++2\,e^-\to H_2;\) \(\displaystyle O^{2-}\to O_2+2e^-\).

A reakció akkor játszódik le, ha elektromos áram folyik a vízbe merülő két elektródán át. Feltehetjük, hogy a reakciókor keletkező mindkét gáz ideális.

A reakcióban keletkező egyik gázt egy kémcsőben fogjuk fel, amin önkényes (nem mm beosztású) skála van. A teljes áthaladó töltés és a kémcsőben lévő gáz térfogatának ismeretében az e/k_B arány meghatározható, ahol e az elektron töltése és k_B a Boltzmann-állandó.

Ez a mérési feladat két részből áll. (Az A és B részeket, továbbá a II. mérést akármilyen sorrendben, sőt egymással párhuzamosan, szimultán módon is elvégezheted. Vedd figyelembe, hogy az elektrolízis lassú folyamat.)

A rész: A kémcsövön lévő önkényes skála kalibrálása dinamikai módszer segítségével. Erre a kalibrálásra szükséged lesz ennek a mérés B részében is, sőt a II. mérési feladatban is.

B rész: Az e/k_B arány meghatározása a víz elektrolíziséből.

A következő ismereteket felhasználhatod:

• A helyi nehézségi gyorsulás: g = (9,78 \(\displaystyle \pm\)0,01) ms^-2.

• A kémcső belső és külső átmérőjének aránya: \(\displaystyle \alpha\)= 0,82\(\displaystyle \pm\)0,01.

A hőmérséklet (T) és a nyomás (P) éppen aktuális értékeit a rendezők fogják megadni.

Az I. mérés (A és B rész) végrehajtásához rendelkezésedre álló eszközök és berendezések:

• Egy kémcső, önkényes (nem milliméter beosztású) skálával.

• Három különböző átmérőjű, szigetelt rézvezeték:

  • 1. nagy átmérőjű barna,
  • 2. kis átmérőjű barna,
  • 3. kék.

• Változtatható feszültségforrás (0-60 V, max. 1 A).

• Egy műanyag tartály és egy üveg víz.

• Egy nehezék, melyen műanyag rögzítő található (ezzel lehet az elektródát a víz alatt a helyén tartani a műanyag szigetelés megsértése nélkül).

• Egy digitális stopper.

• Egy multiméter (ügyelj a helyes használatára).

• Egy fából készült kémcsőtartó, amellyel a kémcsövet függőlegesen lehet tartani.

• Egy pipetta.

• Egy függőleges tartóállvány.

• Fehér javító festék, amellyel jeleket tehetsz megfelelő helyekre.

• Vágóeszköz (kés).

• Olló.

• Ragasztószalag.

• Egy acélgolyó.

• Egy vékony, rozsdamentes acéllap, melyet elektródaként használhatsz.

• (Nem)mm-papír.

Vedd figyelembe, hogy az összes skála a ,,mm-papírokon'' és a kísérleti eszközökön (például a kémcsövön) ugyanolyan skála-osztású, de nem milliméteres.

Mérési feladatok

A rész: A kémcsövön lévő önkényes skála kalibrálása

• Keress egy olyan, jól ismert (dinamikai) módszert, amivel a kémcsőn lévő önkényes skála átszámítható (kalibrálható) mm skálára.

• Add meg azt az egyenletet, ami kapcsolatot teremt a kísérletedben mérhető mennyiségek és a kémcsőre nyomtatott önkényes skála között, és vázold a mérési összeállítást.

• Gyűjtsd össze és használd a mérési adataidat az ismeretlen hossz-skála kalibrálására!

B rész: Az e/k_B arány meghatározása

• Állítsd össze az elektrolízises mérést úgy, hogy abban megfelelő módon legyen a kémcső elhelyezve, hogy a reakcióban keletkező gázok egyikét felfoghasd!

• Vezesd le azt az egyenletet, amely kapcsolatot teremt a következő mérendő mennyiségek között: t idő, I áram, \(\displaystyle \Delta\)h vízszintkülönbség.

• Gyűjtsd össze és elemezd mérési adataidat! Az egyszerűség kedvéért felteheted, hogy a kémcsőben a gáz nyomása a mérés során állandó marad.

• Határozd meg az e/k_B arányt!

II. feladat. Optikai ,,fekete'' doboz

Ebben a feladatban nem kell meghatároznod az eredmények pontosságát, azaz nem szükséges hibaszámítással vagy hibabecsléssel foglalkoznod!

Leírás

Ebben a feladatban egy kocka alakú dobozban elhelyezkedő optikai elemeket kell azonosítanod. A zárt doboz két keskeny nyílással rendelkezik, melyeket vörös színű műanyagfólia fed. Az ismeretlen optikai elemek azonosítása a rendszer optikai viselkedése alapján lehetséges. A nyílásokat fedő vékony műanyagfólia optikai hatása elhanyagolható.

A nyílások középpontjain átmenő egyenest nevezzük a doboz tengelyének. A dobozban (a vörös színű műanyagfólia mögött) három optikai elem helyezkedik el, amelyek között lehetnek azonosak is. Az ismeretlen optikai elemek lehetséges típusai a következők.

• Sík- vagy gömbtükör.

• Gyűjtő- vagy szórólencse.

• Párhuzamos síklapokkal határolt átlátszó lemez (planparalel lemez).

• Prizma.

• Optikai rács.

Az átlátszó optikai elem(ek) anyagának törésmutatója az alkalmazott hullámhosszra 1,47.

A felhasználható eszközök

• Egy 670 nm hullámhosszon működő lézer mutatópálca. (Figyelem: Ne nézz közvetlenül a lézernyalábba!)

• Optikai sín, távolságbeosztás nélkül.

• Az optikai sín mentén mozgatható tartó, amire a dobozt teheted.

• Egy ernyő, ami csatlakoztatható az optikai sín végéhez, de le is választható, és más méréshez felhasználható.

• ,,Milliméterpapír'', melynek távolságegysége nem 1 mm. A ,,milliméterpapír'' ragasztószalaggal az ernyőhöz rögzíthető.

• Függőleges tartóállvány, univerzális befogóval. (Megegyezik az I. mérési feladatnál felhasznált állvánnyal.)

Lehetséges optikai elemek Meghatározandó jellemzők tükör görbületi sugár; a tükör normálisa és a doboz tengelye által bezárt szög lencse* gyűjtő vagy szórólencse; fókusztávolság, elhelyezkedés a dobozon belül planparalel lemez vastagság, a törőoldalak síkja és a doboz tengelye által bezárt szög prizma törőszög, a prizma egyik törőlapja és a doboz tengelye közötti szög optikai rács* rácsállandó, a rácsvonalak iránya, a rács elhelyezkedése a dobozon belül

^* Az említett eszköz csak úgy helyezkedhet el a dobozban, hogy síkja merőleges a doboz tengelyére.

Figyelem! A biztosított ,,milliméterpapír'' távolságegysége megegyezik az I. feladatban használt papíréval, de ez a távolságegység nem 1 mm.

Feladat

Találd ki, hogy milyen optikai alkotóelemek vannak a dobozban (összesen 3 darab), és határozd meg ezek egyéni jellemzőit!

Végső válaszodban az optikai elemek távolság jellegű jellemzőit (például fókusztávolság, görbületi sugár, rácsállandó, stb.) milliméterben, mikrométerben vagy a ,,milliméterpapír'' beosztása által meghatározott egységben add meg.