English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Solution of exercises for practice C

C. 607. The sides of a square are 12 cm long. If the square is rotated through 90^o about the point P, the total area covered by the two squares is 211 cm². If the rotated square is rotated again through 90^o about P, a third square is obtained. The total area covered by the three squares is 287 cm². Where is the point P?

Suggested by G. Bakonyi, Budapest

Solution. The result of the second rotation is the reflection of the original square in the point P. If P is not inside the original square, then the mirror image has no common point with the original one and thus the total area of the three squares must be greater than 2^.144 cm²= 288 cm².

Assume that there is a point P in the interior of the square, such that if the square is rotated through 90^o about P, the total area is 211 cm². The area of one square is 144 cm², and the area of the overlapping part is 2^.144 cm²- 211 cm²= 77 cm². By subtracting the overlapping area from the area of the square, we get 144 cm²- 77 cm²=67 cm².

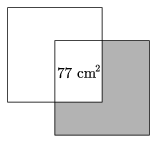
The first rotation increased the area by this amount (the shaded region in the figure). The 2nd square is now rotated about P through 90^o. As the rotated image of the 1st square is the 2nd one, and the rotated image of the 2nd square is the 3rd one, the rotated image of the common part of the 1st and 2nd squares is necessarily the common part of the 2nd and 3rd squares. Thus the total covered area may increase by at most the same amount as the previous time, that is, the covered area cannot exceed 211 cm²+ 67 cm²= 278 cm², as opposed to the given 287 cm². Therefore, no such point P exists.

B. Udvari, Baja