English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Solutions of problems B

B. 3416. A convex polyhedron is bounded by quadrilateral faces, its surface area is A, and the sum of the squares of its edges is Q. Prove that Q\(\displaystyle \ge\)2A.

Proposed by Á. Besenyei, Tatabánya

Solution. First we prove that the sum of the squares of the sides of any quadrilateral is at least four times its area. Using the notations of the figure, the area of the quadrilateral is

\(\displaystyle A_{ABCD}=A_{ABD}\pm A_{BCD}\le A_{ABD}+A_{BCD}=\frac{a\cdot d\cdot\sin\alpha}{2}+\frac{b\cdot c\cdot\sin\gamma}{2}\le\frac{ad+bc}{2}. \)

From the inequality between the arithmetic and geometric means, \(\displaystyle ad\le\frac{a^2+d^2}{2}\) and \(\displaystyle bc\le\frac{b^2+c^2}{2}\), and thus 4A_ABCD\(\displaystyle \le\)a²+b²+c²+d², as stated above.

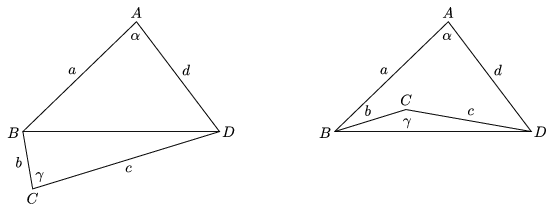
If the corresponding inequality is set up for each face of the polyhedron, and the inequalities are summed, the left-hand side will be 4A, and the right-hand side will be 2Q, as each edge belongs to two faces of the convex polyhedron. Therefore, 4A\(\displaystyle \le\)2Q, and hence 2A\(\displaystyle \le\)Q, and we are done.

Based on the solution by A. Babos, Budapest