 | English Issue, December 2002 | |||
| Previous page | Contents | Next page | ORDER FORM | |
Solutions of problems for physics P
P. 3425. What is the picture of the spoked wheel of a bicycle like on a photo-finish? (The photo finish is made the following way: pictures of a very narrow band around the finish line are made in very short time intervals using electronic camera. These are then placed next to each other at distances corresponding to the expected speed of the bicycle.)
(6 points)
Submitted by: Bodor András, Budapest
Solution. For the sake of simplicity let us take the radius and velocity of the wheel both as 1 unit (in this case the angular velocity is also 1 unit). Let us choose a co-ordinate system where axis x lies in the direction of the horizontal motion of the bicycle and axis y points vertically upwards.
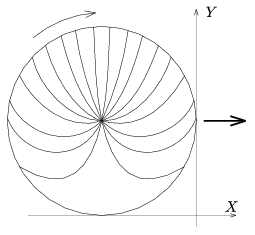
When the axle of the wheel is in point (-1,1) (when the forefront of the wheel touches the finish line where x=0), the equation of a spoke including an \(\displaystyle \alpha\) angle with axis x is: y-1=tan \(\displaystyle \alpha\).(x+1). (We neglected the size of the wheel hub, that is all the lengthened spokes are supposed to go through the axis of the wheel.) After a certain t time the spoke turns by -t angle and the wheel moves t distance in the direction of the positive axis x, so the equation of the spoke will be: y-1=tan (\(\displaystyle \alpha\)-t) .(x-t+1). In the photo-finish those points can be seen that are on axis y, that is those that correspond to the condition x=0 and they are positioned in the height of:
Y=y (t)x=0=1+ tan (\(\displaystyle \alpha\)-t).(1-t),
and their horizontal co-ordinate (corresponding the 1 unit horizontal speed) is X=-t. (Those co-ordinates that give the `virtual reality' of the photo-finish are denoted by capital letters and they are not to be mixed up with the real co-ordinates of the spokes denoted by lower case letters!)
Let us make a graph of the function Y(X)=1+ tan (\(\displaystyle \alpha\)+X).(X+1) with different alpha angles (choose values in 20o steps)! The rim of the wheel looks like a circle in the photo-finish too since a rotation maps a circle into a circle and the proper amount of `electronic displacement' of the points takes their translational motion proportionally into account.
The problem of spokes is not so simple. As can be seen in the figure they are very distorted in these images, and their shape corresponds well to the shape of the spokes on the real electronic photo-finishes (After important bicycle events these can be found and studied on the Internet as well.) (Such a photo-finish can be seen on the home page of KöMaL at the preliminary short solution of the recent problem. The editor.)
Based on the paper of Dőry Magdolna
(10th form student of Ferences Secondary Grammar School, Szentendre)
