 | English Issue, December 2002 | |||
| Previous page | Contents | Next page | ORDER FORM | |
Interesting new characteristics of the electrostatic field
Balázs Pozsgay
There are many important and interesting characteristics of the electrostatic field, such as the spherical symmetry of the field of a point charge or the theorem which states that outside a homogeneously charged spherical shell an electrostatic field generated by it is the same as that of a point charge having the same overall electric charge, and the electric field strength inside the shell is zero. Beyond these well-known features there arose a question in my mind of which I have not heard or read in any book, neither of the proposal nor of the solution of the problem. This problem - mainly after having been considered thoroughly - cast a new light on the characteristics of electrostatic fields (and also of those fields that can be described with similar equations, such as magnetostatic and gravitational fields) for me.
A problem of averaging
The question I was concerned with was: what result do we get in an arbitrary electrostatic field (not necessarily having a spherical symmetry) if we average the electric field strength vector and the electric potential on the surface of an imaginary sphere?
My guess was that the average electric field vector would be the same as the electric field vector in the centre of the sphere and the average potential would be the same as the electric potential in the centre of the sphere. As we will see, the guess is not correct in general, but is not too far from the truth and with a slight modification a true statement can be given.
The `brute force' method
Let us calculate the average of the potential mechanically, that is let us call upon the help of the integral calculus. (If the Reader is inexperienced in this chapter of mathematics, do not put away this paper just skip this section, because in the latter sections there is also an elementary solution offered to this problem!)
Let us first take a field where there is only one point charge and it is in \(\displaystyle \ell\) distance of the centre of the imaginary sphere of radius R. Under the `average' of the U potential we mean the quantity of:
\(\displaystyle U_{\rm{average}}=\frac{\sum_iU_i\cdot df_i}{\sum_idf_i} \)
Interpretation: the surface of the sphere is divided into dfi surface elements (i is an appropriately chosen index of the elements) and the average of the electric potentials detectable on the surface weighted with the size of the surface elements is calculated. (We must emphasize here that dfi means the size of a surface element, a scalar quantity, and it should not be mixed up with the `directional surface element' a vector used in calculating fluxes).
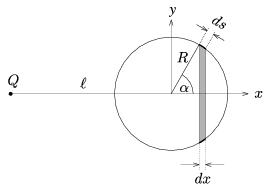
Let us get down to calculation. Take the co-ordinate frame as seen in the figure. The point charge resides on axis x, and let us take the centre of the sphere as the origin. Let us divide the surface of the sphere into belts of width dx. The first step is to determine the size of these surface belts.
\(\displaystyle df=2\pi y\cdot ds=2\pi R\sin\alpha\cdot\frac{dx}{\sin\alpha}=2\pi R\cdot dx. \)
That is, we got that the size of the spherical belts depend only on dx and that makes our further task quite simple. With the above equation the whole surface of the sphere can easily be calculated:
\(\displaystyle F=\sum df=2\pi R\cdot\sum_{x=-R}^{+R}dx=2\pi R\cdot2R=4\pi R^2. \)
In the next step let us calculate the potential in the surface points with x co-ordinates.
\(\displaystyle U=\frac{kQ}{r}, \)
where
\(\displaystyle r=\sqrt{{(\ell+x)}^2+y^2}=\sqrt{{(\ell+x)}^2+R^2-x^2}= \sqrt{\ell^2+2\ell x+R^2}. \)
Now, we can do the integration itself. Since the surface elements with the same distance from the point charge are on a thin spherical belt, it is sensible to divide the sphere into such belts or zones and make the averaging according to these.
\(\displaystyle U_{\rm{average}}=\frac{1}{F}\int U\cdot df= \frac{1}{4\pi R^2}\,2R\pi\cdot kQ\cdot\int_{-R}^R \frac{1}{\sqrt{\ell^2+2\ell x+R^2}}\,dx=\)
\(\displaystyle =\frac{kQ}{2\ell R}\big(|\ell+R|-|\ell-R| \big)= \cases{ \frac{kQ}{\ell},{\rm\ if\ }\ell\ge R,\cr\frac{kQ}{R},{\rm\ if\ }\ell\le R.}\)
We have arrived at a strange formula. Firstly, its form is peculiar, since in the final formula only one is present of the two quantities, R and \(\displaystyle \ell\), and in a symmetric way. Secondly, the physical interpretation is also interesting, because the same formula describes the potential derived from a homogeneously charged spherical shell of charge Q in distance \(\displaystyle \ell\). The present problem under investigation is quite different to that, as it appears, but we will see that there is a close connection between the two (and that can be well exploited).
An elementary solution resulting from energetic considerations
Now let us think that the so far imaginary (or `virtual') spherical shell is an existing (insulator) body which is charged homogeneously with q=1 total charge. What is the interaction energy of this homogeneously charged spherical shell and a point charge of magnitude Q residing in \(\displaystyle \ell\) distance from its centre?
This energy can be determined in two ways. On the one hand, we can calculate the potential derived from the spherical shell in the place where the point charge is located (this can easily be done since the charge distribution has a spherical symmetry) and multiply it with the magnitude of the point charge (Q). The result is well-known, it is exactly the same as the final form of equation (3).
But there is another way. In the spherical symmetric (Coulomb) field of the point charge Q we can calculate the potential energy of the homogeneously distributed charge of the spherical shell. In theory it can be done by dividing the spherical shell into small parts in thought, multiplying the quantities of charge of the surface elements (df), that is df/(4\(\displaystyle \pi\)R2), by the potentials resulting from the Q point charge at the place of the given surface elements, and summing up these energies.
The second method is technically much more difficult than the first one. But fortunately we do not have to go through the complicated summing procedure since its result is obviously the same as that of the first calculation.
N.B. the quantity resulted by the second method is the average potential on the sphere of radius R originated from charge Q. Benefiting from the fact that the two calculations have identical results, the average value in question can be determined with an elementary method leaving out the integral calculus:
\(\displaystyle U_{\rm{average}}=\cases{ \frac{kQ}{\ell},{\rm\ if\ }\ell\ge R,\cr\frac{kQ}{R},{\rm\ if\ }\ell\le R.} \)
The average of the electric field strength vector
The next problem is the averaging of the electric field vector. On the basis of our foregoing results this can be done in two ways. The first method is based on the idea that the field vector is in close connection with the potential, or more exactly with the rate of its spatial variation. This connection can be described in a mathematical form: if from a location where the electric field vector is E we move on with a small \(\displaystyle \Delta\)x displacement vector, the change in the potential will be:
\(\displaystyle \Delta U=-{\overrightarrow{E}}\cdot{\overrightarrow{\Delta x}}. \)
(In the above expression the dot between the two vector quantities means the dot-product of the two vectors, and the negative sign expresses that going in the direction of \(\displaystyle \overrightarrow{E}\) the potential energy decreases.)
From all these it follows that if we know the potential in every location in an electrostatic field, we can calculate the field vector with (5) as well. In a given place the components of the field vector can be calculated by moving out from the given location in the direction of all three co-ordinate axes by \(\displaystyle \Delta\)s displacement and divide the change in the potential with \(\displaystyle \Delta\)s. The resulting three quantities are just the field vector components (except for the sense).
It is not the field vector in a point we would like to determine now but rather the field vector average. Since the components of the average field vector are equal with the average of those consequent components and these can be expressed by the energy variation of the whole sphere due to displacement we can achieve our aim with equations (4) and (5). The x component of the average field vector can be calculated by displacing the sphere along the axis x by \(\displaystyle \Delta\)s, calculating the variation of the average potential in this position and dividing it by \(\displaystyle \Delta\)s. (We exploit here the fact that the change in the average and the average change in the potential are identical.)
Let us see what equation (4) and the above procedure tells us of the average field vector. If the point charge is inside the sphere, we can move the sphere in any direction but the average potential will not change, since it depends only on R and independent of \(\displaystyle \ell\). For this reason, the average field vector on the surface of the sphere is nil. If the charge Q is outside the sphere, the situation is a bit more difficult. However, in this case we can exploit the fact that the average potential is independent of R, so the sphere can be point-like as well. But in this case, the potential energy would be the well known interaction energy of two point charges and the field vector derived by its variation would be equal with the Coulomb filed in the centre of the sphere. Summarizing briefly: The average of the field vector of a point charge on a sphere can be calculated as:
\(\displaystyle
{\overrightarrow{E}}_{\rm{average}}=
\cases{
\frac{kQ}{\ell^2}\cdot\frac{\overrightarrow{\ell}}{\ell},{\rm\ if\ }\el\)R,\cr0,{\rm\ if\ }\ell
Superposition
So far we have dealt with one point charge and the average of its electric field on an imaginary sphere. What is the case if the electrostatic field is generated by several point charges (or a continuous distribution of electric charge)? The resultant electric field is the vector sum (superposition) of the field of the single point-like charges and the average of the sum is the sum of the average of the single constituent fields.
In the previous section we saw that - in the case of a point charge - the average field vector is equal with the field vector detectable in the centre of the sphere. From the superposition principle it follows that the average of the resultant field vector of an arbitrarily complex electrostatic field is equal with the electric field vector in the centre of the sphere generated by the charges residing outside of the sphere. The charges residing inside the sphere do not add to the average. This is the small modification that was not included in the guess-based first form of our theorem. It is interesting that summing according to directed (considered as vector quantities) surface elements (averaging) the situation is just the opposite: the addition of the charges outside of the sphere is nil and the result depends only on the charges inside the sphere, and only these determine the electric flux going through the surface.
Action-reaction
As a conclusion we show that the result obtained for the average of the electric field vector could have been determined more simply without any reference of the potential, with a straight method valid for the most general fields without any symmetry.
Let us suppose that there is an actually existing, evenly charged spherical surface and its overall charge equals the unit charge. In this case, the average of the field vector just equals the force exerted on the sphere by the whole charge system. This force is - according to the action-reaction law - the same as the force exerted on the charge system by the electrostatic field of the sphere with opposite direction. As the sphere is evenly charged, its field corresponds to the field of a point charge (outside of the sphere). So the force is that of a point charge of unit charge exerted on the charges outside of the sphere.
Let us apply the action-reaction principle again: the resultant force exerted on the charges outside of the sphere is equal with the force exerted on a point-like unit charge in the centre of the sphere (apart from the sense), and this equals the electric field vector derived from the outer charges in the centre of the sphere. What is the case with the inner charges? We leave this matter to the reader.
Throughout these considerations we exploited only the inverse square law of the field of a point charge and the superposition principle. The Newtonian gravitational field also possesses these characteristics. And with some further considerations the results are also valid in a magnetic field (Although there is no magnetic pole in Nature, the magnetic field can be describe as if there were separate magnetic poles, and the same kind of laws are valid as in electrostatics). Therefore all of our statements are valid in the same form for the gravitational and magnetostatic fields and also applicable for all `Coulomb-like' vector fields that may be discovered in the future.
