New exercises and problems in Mathematics
January 1998
New exercises for practice in January 1998
C. 489. Joe and Charlie went on an excursion. At the end of their hike they arrived at a highway and decided to take a bus. Joe continued to walk forward to the next bus-stop at a speed of 4 km/h, while Charlie assumed that the previous stop was closer by, and thus headed in the opposite direction at a speed of 6 km/h. They each arrived just on time to catch the bus. Find out if Charlie's assumption was right, given that the bus travelled at a speed of 60 km/h.
C. 490. Prove that the difference between any two odd perfect squares is divisible by 8.
C. 491. Prove that every triangle has at most one such side which is smaller than the corresponding altitude.
C. 492. We measure the angles of inclination of a tower, emerging on level ground, at distances of 50 m and 100 m from its base, respectivley. The two measures sum up to 45o. Determine the height of the tower.
New exercieses in January 1998
Gy. 3174. Ann and Bob play the following game. First they draw an nxn square and colour its horizontal sides with red and its vertical sides with blue. Ann starts the game and then they move alternately. At each move, Ann (Bob) chooses a small square which is not yet coloured and which already has at least one red (blue) side, and colours it with red (blue). The game ends when either Ann (Bob) connects the horizontal (vertical) sides with a chain of red (blue) fields such that any two consecutive ones share a common edge, in which case she (he) wins the game, or when a player, whose turn it is, cannot move, in which case the game is a draw. Determine those values of n for which one of the two players has a winning strategy.
Gy. 3175. Let a and b denote positive numbers. Prove
inequality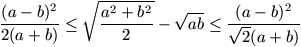 
.
Gy. 3176. Define a sequence (ai) by
a1=0, a2=2, a3=3,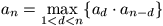 
for n=4,5,6,... Find
a1998.
Gy. 3177. There are two Hungarian teams, the Bolyai TC and the E\"otv\"os TK, among those qualified for the 16 best teams in the Europe Cup. How likely is that they are going to play against each other? (After each match, one team qualifies for the next round and the other one is eliminated from the contest.)
Gy. 3178. In a triangle of unit area, what is the smallest possible length of the second largest side?
Gy. 3179. The vertices of tetrahedron BRYG are coloured with blue, red, yellow and green, respectively. Next, the edges of the tetrahedron are coloured such that all the four colours are used and the colour of each edge agrees with the colour of one of its vertices. Prove that there can be found a vertex such that either the three edges starting at that vertex or the other three edges have the three colours blue, red and green, respectively.
Gy. 3180. Let a,b,c be the sides of a
triangle. Given that the area of the triangle is
(a-b+c)(a+b-c), prove that
the length of the angle bisector opposite to side a is
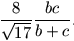
Gy. 3181. In a right square based pyramid, the centres of the inscribed and circumscribed spheres coincide. Find the angle formed by any two neighbouring lateral edges.
New problems in January 1998
F. 3208. Given that the positive numbers x, y, z satisfy x2+xy+y2=9, y2+yz+z2=16, z2+zx+x2=25, determine xy+yz+zx.
F. 3209. Consider a connected graph on n vertices and assign a real number to each edge of the graph which is to be called the value of that edge. For any path of the graph, the value of the path is defined as the largest value of any edge along the given path. For any two vertices x,y of the graph, let f(x,y) denote the smallest possible value of a path connecting x with y. Prove that the cardinality of the range of f is not greater than n-1.
F. 3210. Is it possible that the range of a polynomial of real
coefficients in two variables is the (open) interval
?
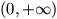F. 3211. Let n>2 be an integer and
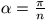. Prove equality
.
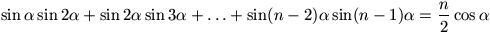F. 3212. In a triangle ABC, F denotes the midpoint of side BC and E denotes the common point of BC and the angle bisector starting at A. The circumcircle of triangle AEF intersects sides AB and AC at points B1 and C1, respectively. Show that BB1=CC1.
F. 3213. Consider two skew lines wich are extensions of two edges of a cube, respectively. A unit segment is placed arbitrarily along each line. In which position of the two segments has the tetrahedron determined by their endpoints a maximum volume?
New advanced problems in January 1998
N. 159. Prove that every convex n-gon can be dissected, with nn-3 pairwise non-crossing diagonals, into triangles such that no vertex of the polygon is inside the circumcircle of any triangle.
N. 160. A sequence (an) is defined by
a0=a1=0, a2=1 and
an+3=an+1+1998an.
Prove that equality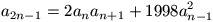 
holds for every
positive integer n.
N. 161. The coefficients of a polynomial p are integers whose absolute values are not greater than 1998. Given that p(2000) is a prime number, prove that p cannot be written as a product of two polynomials, each of positive degree and of integer coefficients.
N. 162. The complete graph G on n vertices is to be decomposed as a union of complete bipartite graphs such that each edge of G belongs to exactly one of the bipartite graphs. Find the minimum number of bipartite graphs needed for such a decomposition.