New exercises and problems in Mathematics
February 1998
New exercises for practice in February 1998
C. 493. Find all perfect squares with the following property: if we divide them by 11, the (partial) quotient is a prime number and the remainder is 4.
C. 494. Write the numbers 1,2,...,n in a row, in increasing order. In the next row, write the same numbers in decreasing order. Consider the difference of any two numbers, one of which is lying below the other. Determine the sum of the absolute values of all such differences.
C. 495. Prove that if the base angles of a trapezoid are not congruent, then the diagonal starting at the vertex of the smaller angle is longer than the other diagonal.
C. 496. The diagonals of a regular hexagonal prism have lengths 12 and 13. Calculate the volume of the polyhedron.
New exercieses in February 1998
Gy. 3182. The non-negative real numbers a,b,c,d add up
to 1. Prove inequality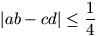 
.
Gy. 3183. Some people, who know each other very well, are sitting at a round table. Some of them always tell the truth, but the others always lie. Each of them claims that he is veracious, but the kth person sitting on his right hand side is a liar. How many people can be there around the table?
Gy. 3184. In America, temperature is measured in Fahrenheit degrees. This is a linear scale in which the melting point of ice is taken as 32 degrees (32 oF) and the boiling point of water is taken as 212 oF. Someone gives us the temperature in Fahrenheit degrees, rounded to the nearest integer degree. We then convert it to the Celsius scale and round it to the nearest integer degree. Express, in centigrades, the maximum possible deviation of the temperature calculated this way from the actual temperature.
Gy. 3185. The numbers 1,2,...,n are assigned, in some order, to the vertices A1, A2, ..., An of a regular n-gon.
- a) Prove that the sum of the absolute values of the differences
between adjacent numbers is at least 2n-2.
- b) Find the number of arrangements in which the above sum is exactly
2n-2.
Gy. 3186. Construct a triangle, given the lengths of an altitude and a median, starting at the same vertex of the triangle, and the distance between that vertex and the orthocentre of the triangle.
Gy. 3187. Ann and Bob agreed to have a date somewhen between 5 and 5:30 p.m. Assuming that they arrive within the specified interval, find the probability that no one has to wait more than 10 minutes for the other.
Gy. 3188. Prove that every tetrahedron has a vertex such that the edges starting at that vertex can be rearranged to form a triangle.
Gy. 3189. Rotate a cube of unit edge by 60o about one of its diagonals. Calculate the volume of the intersection of the rotated cube with the original one.
New problems in February 1998
F. 3214. Aladdin walked all over the equator in such a way that in each moment he either was moving to the west or was moving to the east or applied some magic trick to get to the opposite point of the Earth. We know that he travelled at most 19000 km's alltogether during his westward moves. Prove that there was a moment when the difference between the distances he had covered moving to the east and moving to the west, respectively, was at least half of the length of the equator.
F. 3215. We are given real numbers
a1, a2, ..., an
such that each of them is greater than a positive number k.
Prove inequality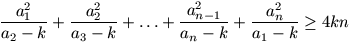 
.
F. 3216. Decide, whether inequality
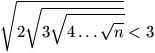holds for every natural number
n.
F. 3217. Let s1, s2, s3 denote the lengths of the medians in a triangle, and let d1, d2 and d3 denote the distances of a point P from the medians, respectively. Prove that one of the products s1d1, s2d2 s3d3 equals the sum of the other two.
F. 3218. We are given a triangle A1A2A3 and a point P inside the triangle. Let Bi, for i=1,2,3, denote the foot of the perpendicular from P to line AiAi+1 (indices are taken modulo 3). In a similar manner, we can obtain a triangle C1C2C3 from triangle B1B2B3, and then triangle D1D2D3 from triangle C1C2C3. Prove that triangle D1D2D3 is similar to triangle A1A2A3.
F. 3219. Each face of a regular dodecahedron is coloured with one of four colours, red, blue, yellow and green, such that adjacent faces have different colours. Find the number of such edges for which one of the two faces incident to the edge is blue and the other one is green.
New advanced problems in February 1998
N. 163. Consider words of length 3n obtained from a
three letter alphabet A,B,C according to the
folllowing rules. Firstly, each letter has to be used exactly n
times. Secondly, for each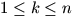 
, the
kth letter `A' has to precede the kth letter
`B', which, in turn, has to precede the kth letter
`C'. Prove that the number of such words is
.
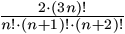N. 164. Is there any number in the Fibonacci sequence whose six last digits (in decimal system) are all 9?
N. 165. Sets A0, A1,
A2, ..., Ak are subsets, each of
size 2n, of a set of 4n elements. Prove that there can be
found two of them whose intersection has at least
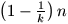elements.
N. 166. We are given four points on a line in the following order: A,B,C,D. Moreover, we know that AB=CD. Is it possible to construct the midpoint of segment BC, if we are only allowed to use a straightedge?