New exercises and problems in Mathematics
April 1998

New exercises for practice in April 1998

C. 501. One morning in the school the integers from 1 through a certain number were written on the blackboard. A student carefully erased one of them. There would have been nothing special about it if someone had not noted that the average of the remaining numbers had been 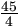. Try to figure out which number was erased.

C. 502. Let us denote the roots of equation x²-2bx+b²-c²=0 by x₁ and x₂. Prove that the roots of equation x²-2b(b²+3c²)x+(b²-c²)³=0 are 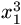and .

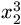C. 503. Given are two isosceles triangles. The inscribed circles of the triangles touch the legs at their points of trisection closer to the base of the triangle in one case and further from the base of the triangle in the other case. In which case covers the inscribed circle a greater portion of the area of the triangle?

C. 504. The points A, B, C, D, E, F lie in the 3 dimensional space. How are the points positioned if there exists a plane, in the same distance from each of the points, which separates points A, B, C from points D, E, F?

New exercieses in April 1998

Gy. 3198. Do there exist positive integers a, b, c, d such that ab=cd and a+b+c+d is a prime number?

Gy. 3199. Find all integer solutions to equation 1996x+1998y+1=xy.

Gy. 3200. Let H be a 1000-element subset of the set {0, 1, 2, ..., 1998}. Prove that it has two not necessarily distinct elements a and b such that a+b is a power of 2.

Gy. 3201. A 9x9 chessboard is is packed with 1x2 dominoes such that only one corner of the board is left uncovered. Prove that the uncovered field of the board can be transferred to any other corner by shifting the dominoes about on the board.

Gy. 3202. A solid cube of edge length n cm is divided into smaller cubes each with egde length 1 cm. Determine those values of n for which a subset of the small cubes can be arranged to form a cube with edge length 2n cm. The latter cube may be hollow.

Gy. 3203. The lengths of the diagonals of a rhomboid are 2a and 2b, respectively. The sides of the rhomboid together with those tangents of the inscribed circle which are parallel to either diagonal form an octagon. Express the area of the octagon in terms of a and b.

Gy. 3204. The segments AB and CD are parallel. P is an interior point of segment BC, the lines AP and CD intersect in E. For which point P is the sum of the areas of triangles APB and CPE is minimum?

Gy. 3205. Semicircles are drawn externally on each side of the acute triangle ABC. The altitudes drawn from vertices A,B,C intersect the semicircles in points E,F,G, respectively. Prove that the hexagon AGBECF can be folded into a pyramid of base ABC.

New problems in April 1998

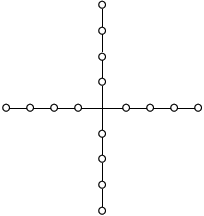
F. 3226. In how many different ways can one colour the circles depicted on the figure such that each arm contains exactly two yellow and two blue circles? Two colourings are different if one cannot be obtained from the other using a rotation or a reflection.

F. 3227. Find all values of m for which polynomial x^m+y^m+z^m-(x+y+z)^m is divisible by (y+z)(z+x)(x+y).

F. 3228. A bus line connects cities A and B. The buses leave in every 30 minutes. Each bus has a capacity of 50 passengers. Those who do not fit in the bus wait in the waiting hall, and those passengers who do not even fit there leave for B on foot. Between two consecutive buses either 0, 25, 50 or 75 passengers arrive, with probability 1/4, respectively. A new waiting hall is to be built to replace the old one. It is to be built from modules, each of capacity 25. At least how many such modules have to be used in order to ensure that the probability that one has to leave on foot is smaller than 1%?

F. 3229. In a triangle of side lengths a,b,c, the exradius belonging to side c is the geometric mean of the exradii belonging to sides a and b, respectively. Express c in terms of a and b.

F. 3230. Let S denote the centroid of triangle ABC. Erect perpendiculars from each vertex of the triangle to the external and internal bisectors of the angles belonging to the other two vertices. Prove that the sum of the squares of the lengths of the resulting perpendicular segments is 6(SA²+SB²+SC²).

F. 3231. Given are a sphere g and a point P in its interior. Let h₁, h₂ és h₃ be pairwise orthogonal chords passing through P. Each of the three planes determined by the pairs of chords intersect the sphere in a circle. Prove that the sum of the areas of the three circles is independent of the position of the chords.

New advanced problems in April 1998

N. 171. There are given lines e₁, e₂, ..., e_n and a point P in the plane. Project P perpendicularly on the first line. Next, project its image on the second line, and so on. After projecting on the last line, project again on the first line, and continue the process. Prove that the different images obtained by the procedure form a bounded set.

N. 172. An automatic card shuffler is used to shuffle a deck of 2n cards. It can rearrange the deck according to the rule (1, 2, 3, ..., 2n-1, 2n)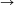(2n, 1, 2n-1, 2, ..., n+1, n). Prove that the cards will be in their original order after at most 2n shuffles.

N. 173. Is it possible to partition a 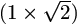rectangle into a finite number of squares?

N. 174. A tour of a tree graph is the following. A figure, moving along the edges of the graph, visits each vertex such that it travels along every edge exactly twice. We say that two figures tour the graph simultaneously if they start at the same time, not necessarily at the same vertex, and then they always move at the same time during their respective tours of the graph. They meet if they move to the same vertex or stay on the same edge of the graph at the same time. Let f(n) denote the largest integer for which there exist a tree on n vertices which f(n) figures can tour simultaneously such that no two of them meet. Prove that f(5k+1)=2k for every positive integer k.