New exercises and problems in Mathematics
September 1998
 |
New exercises for practice in September 1998 |
C. 509. An escalator has 125 stairs. Walking upwards while the escalator is going up at a constant speed, once we reached the upper end of the escalator after making 45 steps. Next time we were able to make 55 steps before reaching the top of the escalator. How much faster were we walking the second time?
Fried Ervin (Budapest)
C. 510. Let A be a ten-thousand-million-digit number divisible by 9. Let B denote the sum of the digits of A and let C denote the sum of the digits of B. Determine the sum of the digits of C.
C. 511. A certain parallelogram has 4 cm and 7 cm long sides. The lengths of its diagonals differ by 2 cm. How long are the diagonals of the parallelogram?
C. 512. After the guests had left the party, a piece of a cake, in the shape of a quarter of a circle of radius 15 cm, was still lying on the table. We cut two 1.5 cm wide strips off the cake, parallel to each straight edge of the piece, and ate them up. What fraction of the piece of the cake did we consume?
 |
New exercieses in September 1998 |
Gy. 3214. At a party, one is called `timid' if he or she knows at most 3 other people. Prove that if everybody at the party has at least 3 timid acquaintances, then everybody is timid. How many participants may be there at the party in this case?
Gy. 3215. For any integer n, let \(\displaystyle sigma" ALIGN=ABSCENTE\)(n) denote the sum of its positive divisors. (For example, \(\displaystyle sigma" ALIGN=ABSCENTE\)(3)=1+3=4, \(\displaystyle sigma" ALIGN=ABSCENTE\)(6)=1+2+3+6=12.) Prove or disprove: if \(\displaystyle sigma" ALIGN=ABSCENTE\)(n)>2n, then \(\displaystyle sigma" ALIGN=ABSCENTE\)(m)>2m for every multiple m of n.
Gy. 3216. Find those pairs a, b for which equations
- 19x2+19y2+ax+by+98=0
- 98x2+98y2+ax+by+19=0
Gy. 3217. Find those prime numbers p for which the system
- p+1=2x2
- p2+1=2y2
German competition problem
Gy. 3218. Let A and B denote two points of a circle centered at a point O, and let P be a point inside the circle, different from O. Construct points C and D on the circle such that triangles PAB and PCD are similar to each other and have the same orientation.
Based on the submission of Bohner Géza (Cegléd)
Gy. 3219. Each side of a convex quadrilateral is tangent to a circle of radius r whose centre is denoted by O. Show that at least one of the circles, circumscribed to triangles OAB and OCD, respectively, has a radius larger than or equal to r.
Gy. 3220. A cyclic trapezium has bases a and b, a<b. The angle at one vertex of the longer base of the trapezium, subtended by the shorter base, measures 45o. Determine the area of the trapezium.
Gy. 3221. Prove that six congruent regular octahedra and eight regular tetrahedra, all of the same edge-length can be arranged to form a regular octahedron whose edges are twice as large as those of the original polyhedra.
 |
New problems in September 1998 |
F. 3238. Prove that inequality
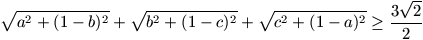
holds for arbitrary real numbers a, b, c.
F. 3239.
Find those natural numbers x, y which satisfy equality x2(x2+y2)=y100.
F. 3240.
Show that there exist infinitely many pairs a, b
of positive integers such that a divides
b2+b+1 and b divides
a2+a+1.
F. 3241.
In a triangle ABC, points
A1,
B1 and
C1 are incident to sides CB, AC and AB,
respectively, such that
Let r1, r2, r3,
r4 and r denote the radii of the inscribed
circles of triangles
AC1B1,
BC1A1,
CA1B1,
A1B1C1 and ABC,
respectively. Determine those values of \(\displaystyle lambda"
ALIGN=ABSCENTE\) for which equality
holds.
Bíróo Bálint (Eger)
F. 3242.
The distance between a (closed) region K and a point
P is defined as the minimum of all distances PQ, where
\(\displaystyle Q eleme K-nak" ALIGN=ABSCENTE\).
Given are in the plane a square and a circle outside each other such that the
centre of the circle lies on the extension of one of the sides of the
square. Determine the locus of points which lie in the same distance from the
circle and the square.
F. 3243.
Let a, b, c, d be pairwise skew lines in three
dimensional Euclidean space such that the normal transversals of a,
b and c, d are orthogonal to each other, and so are the
normal transversals of a, c and b, d, too. Prove
that the normal transversals of a, d and b, c are
also orthogonal to each other.
N. 179.
Given 3 collinear points in the plane, show that, for every positive integer
n, it is possible to draw n distinct concentric circles around
each point such that the number of points which are incident to 3 circles is
at least cn2, where c is a positive constant
independent of the position of the given points.
N. 180.
In a trapezium ABCD, the intersection of diagonals AC and
BD is denoted by F. Point E is incident to leg AD
such that EF is parallel to AB. There are given two parabolas
whose axes are parallel to the bases of the trapezium. One of them passes
through points B, C, E, the other touches lines
AD, BD, AC. Prove that the parabolas touch each other.
N. 181.
Given are a few balls in the three dimensional Euclidean space whose interiors
have a point in common. These balls are rearranged in such a way that the
distance between the centres of any two of them decreases. Prove that in their
new position, the balls still have a common interior point.
N. 182.
Find all pairs a, b of positive integers for which
a divides b2+b+1 and
b divides a2+a+1.
Fried Ervin (Budapest)
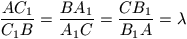 .
.

New advanced problems in September 1998

