 |
Exercises and problems in Physics |
New experimental problem:
m. 204. Observe the motion of balls started from the side of a bath wiped dry and bunged. Due to the slope of the bottom of the bath, the balls moving to and fro drift towards the bung. How does the average drift velocity in the direction of the slope of the bath depend on the height h of the starting point? Make experiments using balls of different material and size (e.g. steel ball, glass ball, table-tennis ball, etc.), and using different starting points with the same height h as well. (6 points)
New exercises:
FGy. 3224. 5 cm3 of water is mixed with 5 cm3 of heavy water in one vessel, and 5 g of water is mixed with 5 g of heavy water in another one. Which mixture is of higher density? (3 points)
FGy. 3225. A bus driver is separated from the passengers by a Plexiglas pane mounted behind him. A car moving at a speed of 110 km/h starts to overtake the bus travelling at a speed of 80 km/h. In what direction and at what speed does the reflection of the lights of the car made by the Plexiglas pane move, as seen by a passenger on the bus? (3 points)
FGy. 3226. An inert gas with a volume of 2 dm3 and a pressure of 105 Pa expands to a volume of 6 dm3 in such a way that the process can be represented on a (p,V) diagram by a straight line. At the end of the process, the increase of the internal energy of the gas is twice the work done by the gas.
- a) Determine the pressure of the gas in the final state.
b) How much heat does the gas take up during the expansion? (4 points)
FGy. 3227. An astronaut throws a stone on the Moon at an angle of 60o with the horizontal and at an initial speed of 20 m/s. What are the tangential and the normal components of the acceleration of the stone 3 seconds after the throwing? What is the radius of curvature of the trajectory in this point? (5 points)
New problems:
FF. 3228. A small body of mass m can be fastened to any point of a homogeneous rod of length l and mass M suspended at one end. Where should the small body be fixed so that the period of the rod is minimum? What is this minimum period? (E.g. let m=6M.)
FF. 3229. A body starting from the top of a slope of
inclination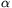 
and height h
slides down the slope and rebounds from a wall perpendicular to
the slope. It loses some mechanical energy both while sliding and
while rebounding. What distance does it cover in how much time before
it finally stops? The coefficient of dynamic friction is 
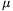, the collision number (the ratio of the
speeds after to before rebounding) is k. Numerical data: 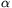=30o,
h=1 m, =
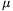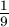, k=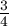
.
FF. 3230. The top plate of a charged plane capacitor is fixed, while the bottom one is kept in equilibrium by the gravitational and electrostatic forces. What is the type of the equilibrium when a) the charge, b) the pd. of the capacitor is constant?
FF. 3231. A metal ring with a mass of 1 gram and a charge of 2.10-8 C rotates at high velocity about its symmetry axis perpendicular to its plane. Calculate its magnetic dipole momentum if its momentum is 0.1 kg m2 s-1.
New advanced problem:
FN. 3232. On a slope of inclination 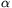, the coefficient of friction grows proportionally to
the distance from the top of the slope: =
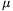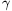.x. Describe the motion of a tyre of
mass m and radius r starting from the top of the
slope. In how much time will the tyre start rolling without friction?