New exercises and problems in Mathematics
February 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in February 2000 |
C. 570. Find those 3-digit prime numbers whose digits multiply up to 189.
C. 571. The side of a square based doghouse is 1.2 m long. A dog on a 3 m long leash is tied to the doghouse such a way that the end of the leash is fixed to the entrance side of the house, in a 0.3 m distance from its corner. Calculate the area of the region the dog can reach.
C. 572. A square and a regular hexagon are inscribed in a circle whose radius is 6 cm such that one side of the hexagon is parallel to a side of the square. Calculate the area of a segment of the disc which lies between two such parallel sides and does not contain the centre of the circle.
C. 573. Find those positive integers n for which 12+22+...+n2=1+2+...+(2n-1)+2n.
C. 574. What relations must the edges of a rectangular box satisfy if it can be cut into two congruent rectangular boxes, each similar to the original one.
 |
New problems in February 2000 |
B. 3342. Find those positive integers n for which n2-19n-99 is a perfect square. (3 points)
American problem
B. 3343. In a triangle ABC, the midpoint of side AB is denoted by F. Points S1 and S2 are the centroids of triangles AFC and BFC. Lines AS1 and BS2 intersect sides BC and AC, respectively, at points P1 and P2. Prove that the quadrilateral S1S2P1P2 is a parallelogram. (3 points)
B. 3344. There are certain positive integers the number of whose divisors can be obtained by subtracting the product of the indices of their prime divisors from the product of the prime divisors. Such integers are, for example, 25 and 600. Prove that there are infinitely many such integers. (4 points)
B. 3345. 9 teams were participating in a (one-round) soccer tournament. The Devonshire Bulls won 5 games and lost the other 3 games. Is it possible that they finished at the 7th place? (At such a tournament, the winner of a game scores 3 points, while in case of a draw game both teams score 1 point. If two teams have the same total number of points in the end, they are ranked according to the difference of the goals, scored and got by the respective teams.) (4 points)
B. 3346. 100 weights, measuring 1,2, ..., 100 grams, respectively, are placed in the two pans of a scale such that the scale is balanced. Prove that two weights can be removed from each pan such that the equilibrium is not broken. (5 points)
Tournament of Towns, 1999.
B. 3347. Consider a quadrilateral as
a) the quadruple of its four vertices;
b)) a homogeneous lamina.
In both cases one can determine the centroid of the quadrilateral. Find those quadrilaterals, for which the two centroids coincide.
Proposed by: Z. Bogdán, Cegléd
B. 3348. Find all integer solutions of the equation
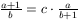(4 points)
Proposed by: E. Fried, Budapest
B. 3349. Prove that the equation
pp=qq admits an infinite number of positive
rational solutions with p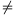
q.(5 points)
Proposed by: L. Lóczi, Budapest
B. 3350. A point P is given inside a rectangular box. Reflect P in each face of the box. Describe that position of P for which the convex polyhedron determined by the six mirror images has maximum volume.(3 points)
B. 3351. At least four circles are given in the 3-space such that no 4 of their centres lie in the same plane. Moreover, any two circles lie on a common sphere. Is it necessarily true that all circles lie on the same sphere? (5 points)
 |
New advanced problems in February 2000 |
A. 230. Find all integers a for which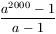 
is a perfect square.
A. 231. In a connected simple graph every vertex has a degree at least 3. Prove that the graph contains a cycle such that the graph remains connected when the edges of this cycle are deleted.
Proposed by: T. Kiss, Budapest
A. 232. Construct a convex polyhedron with at least 2000 vertices whose edges are not shorter than 1/2, but it can be placed in a sphere of unit radius.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.