A 2000. márciusi C-jelű matematika gyakorlatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaLban folyamatosan közöljük.
C.575. "Nos, hát mondja meg nekem, hogy ha Pozsonyból
Brassóba mindennap két postakocsi közlekednék, Brassóból Pozsonyba
pedig ugyanannyi, ha mármost föltesszük, hogy az út tíz napig tart,
mennyi kocsival találkozik ön útközben, míg Pozsonyból egy postakocsin
ülve Brassóba ér?" 
Javasolta: Mikszáth Kálmán, Fogaras
Az idézet folytatása:
- Hússzal.
- Nono, fiatalember, gondolja meg jól, nem annyival.
- Akkor talán valami furfang van a kérdésben?
- Biztosítom, hogy nincs.
- Ez esetben kétségtelenül húsz, vagyis hogy az egyik, a huszadik már éppen beért Pozsonyba, mikor én onnan elindultam, tehát csak tizenkileccel! Nem igaz?
- Nem és nem. Igen sajnálom kedves, ifjú barátom.
- Engedje meg, uram, hogy nyugodtan kiszámítsam a szobámban.
- Tessék - mondá az öregúr gúnyos mosolygással.
A brünni vállalkozó egész nap számított, őrülten számított, teleírt számokkal vagy tíz ív papírt, a homlokáról csurgott az izzadtság, annyit számított, de nem boldogult, mindig más-más eredmény jött ki. Végre egy szakajtó babot kért a szakácsnétól, a babszemekből aztán kirakta az induló postakocsikat a pozsony-brassói vonalon, de csak még jobban belezavarodott az egészbe. Mikor aztán látta Horváth, hogy semmire sem megy, megszabadította a bizonytalanságtól.
- Hát lássa, önből nem lesz jó vállalkozó, mert ön nem látja tisztán maga előtt a dolgok következményeit már a második fokon sem. A pozsony-brassói úton ott vannak az előző tíz napon elindult szekerek is, meg a mostani tíz napon elindultak. Eszerint a pozsony-brassói úton negyven szekér van. Ami pedig az ön mostani útját illeti, ne haragudjék, de azon csak egy kosár van.
C.576. Adjuk meg azt a legkisebb pozitív egész számot, amellyel az 1999-et megszorozva a kapott szám utolsó 4 jegye 2001.
Braun Melinda ötlete, Szeged
Megoldásvázlat.
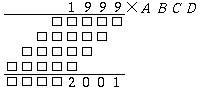
A feladat az, hogy az ábrán az A, B, C, D betűk és a négyzetek helyére számjegyeket írjunk úgy, hogy a papíron szorzás szabályai teljesüljenek.
A szorzat utolsó jegye 1, ezért D-t úgy kell megválasztanunk, hogy 9xD utolsó jegye 1 legyen; ez csak D=9 esetén igaz. Beírva D=9-et, az ábra a következőképpen alakul:
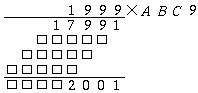
Ahhoz, hogy a szorzat utolsó előtti számjegye 0 legyen, az szükséges, hogy 9xC utolsó jegye 1 legyen, ezért C=9:
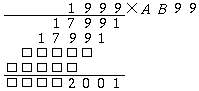
Teljesen hasonlóan kapjuk, hogy B=9:
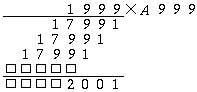
Végül A=5:
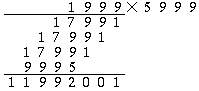
Tehát az 5999 a legkisebb pozitív egész, amellyel az 1999-et szorozva a kapott szám utolsó 4 jegye 2001.
C.577. Egy fiók mélyén három pár zokni van, amelyek kissé különböznek egymástól. A fiókból egyesével kihalászva a zoknikat, mennyi annak a valószínűsége, hogy három húzás után még nem lesz a kivett zoknik között összetartozó pár?
1. megoldásvázlat. Összesen 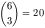 -féleképpen választhatunk ki a 6 darab zokniból
3-at. Azoknak az eseteknek a száma, amikor nincs egyetlen pár sem
2.2.2=8, mert mindegyik párból egyet-egyet kell
kiválasztani. A keresett valószínűség tehát
-féleképpen választhatunk ki a 6 darab zokniból
3-at. Azoknak az eseteknek a száma, amikor nincs egyetlen pár sem
2.2.2=8, mert mindegyik párból egyet-egyet kell
kiválasztani. A keresett valószínűség tehát 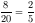 .
.
2. megoldásvázlat. Sorban kihúzva a 3 zoknit, a második zoknit 5 darab közül kell kiválasztanunk, amelyek közül az egyik a már kihúzott első zoknival azonos, a többi 4 darab attól különböző színű. A második zokni tehát 4/5 valószínűséggel, tehát az esetek 4/5 részében lesz az elsőtől különböző. Ha a két különböző zokninkhoz húzunk egy harmadikat, azt 4 darab közül választjuk ki, ezek közül 2 olyan színű, amilyet még nem húztunk. Ezért a harmadik zokni 2/4 valószínűséggel lesz a harmadik fajtából. Tehát az összes eset 4/5 részében lesz különböző az első két zokni, és ezen esetek 2/4 részében lesz a harmadik is különböző. A keresett valószínűség tehát 4/5 x 2/4 = 2/5.
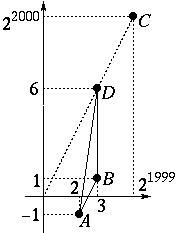
C.578. Egy háromszög csúcsainak koordinátái: A(2;-1), B(3;1), C(21999;22000). Számítsuk ki az ABC háromszög területét.
Megoldásvázlat. Az AB egyenes meredeksége 2. Ha C-n egy ugyanilyen meredekségű egyenest fektetünk, az átmegy az origón és a D(3;6) ponton. Ezért az ABC háromszög területe megegyezik az ABD háromszög területével, amelynek BD alapja 5 egység, A-ból induló magassága 1 egység hosszú. A háromszög területe tehát 2,5 egység.
C.579. Egy körlapot két sugara mentén két darabra vágunk. A kapott körcikkekből kúp alakú tölcséreket formálunk. Akkor lesz-e legnagyobb a tölcsérek össztérfogata, ha félkörökből indulunk ki?
Megoldásvázlat. Legyen a körlap sugara r, a két darab
középponti szöge (1+x)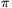 és
(1-x)
és
(1-x)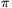 , ahol |x|<1.
Könnyen ellenőrizhető, hogy a két kúp alapkörének sugara
(1+x)/2 és (1-x)/2, magasságuk
, ahol |x|<1.
Könnyen ellenőrizhető, hogy a két kúp alapkörének sugara
(1+x)/2 és (1-x)/2, magasságuk
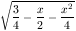 illetve
illetve 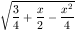 . A térfogatok összege
. A térfogatok összege
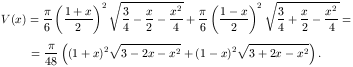
Könnyű ellenőrizni, hogy V(0)=2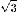
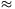 3,4641 nem a
legnagyobb értéke a fügvénynek; pl. V(0,1)
3,4641 nem a
legnagyobb értéke a fügvénynek; pl. V(0,1)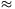 3,4678 nagyobb. (A függvény maximuma a 0,352 szám
közelében van, értéke közelítőleg 3.4885.) Tehát a válasz a kérdésre: nem!
3,4678 nagyobb. (A függvény maximuma a 0,352 szám
közelében van, értéke közelítőleg 3.4885.) Tehát a válasz a kérdésre: nem!

