 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
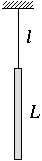M. 215. A
homogeneous rod of length L is suspended onto a thread of
length l. Measure the two eigen-frequencies of the system for
different values of L and l. (Consider only plane
motions.)
New problems:
P. 3334. A boy usually rides his bicycle along a certain route at a constant speed. He once makes the first x percent of this route at a speed x percent lower than usual. Then he makes the rest of the distance at a speed twice as high as usual, and arrives at his destination at the usual time. How many percents of the total distance does he make at a speed lower than usual in this case?
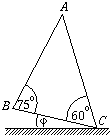P. 3335. Point-like
bodies can slide without friction from vertex A along sides
AB and AC of the triangle ABC shown in the
figure. What should the angle 
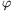shown in the figure be so that the bodies released from point A
with no initial velocity arrive at points B and C at
the same time?
P. 3336. The gas in a Diesel engine is adiabatically compressed. If the initial temperature is 27 oC then the temperature after the compression is 681 oC. Assume that the gas can be considered as an ideal gas consisting of diatomic molecules. What is the proportion of the volumes of the gas before and after the compression?
P. 3337. The energy of a drop of mercury (considered as
spherical) at rest on a level table can be given by the following
formula: E=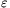
V+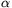
A+mgr (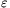>0 is a constant, 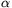is the surface tension of mercury, and r is
the radius, A the surface, V the volume and m the
mass of the drop). What is the radius of the drop of mercury giving
the lowest specific energy (energy per unit mass)? Determine the
radius numerically as well.
P. 3338. The tube of
cross-section A closed at one end by soldering (shown in the
figure) is in a vertical plane. The column of mercury of length L
situated in the horizontal part of the tube blocks a column of
oxygen of length L. The external pressure is identical to the
hydrostatic pressure of a column of mercury of height L. The
temperature around the tube slowly rises. What is the volume of the
gas when the work done by the gas is 20 % of the absorbed heat? (The
vertical part of the tube is sufficiently long.)
P. 3339. Two metal balls of radius R are placed at distance r from each other (r<<R). One has charge Q1, the other one charge Q2. What is the maximum energy converted into heat in the wire connecting the two metal spheres? Data: Q1=3.10-8 C, Q2=2.10-9 C, r=2 m, R=2 cm.
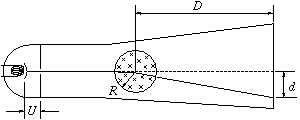P. 3340. A homogeneous
magnetic field of circular cross-section with radius
R=2 cm is formed inside a cathode ray tube, using a
coil. When the coil is switched on, the deviation of the electron beam
accelerated using a potential difference U=250 V is
d=10 cm on a screen at distance D=20 cm from
the axis of the coil. What is the induction of the deviating magnetic
field? (The beam crosses the axis of the coil before switching the
coil on.)
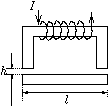P. 3341. The
cross-section of the U-shaped iron core of an electromagnet is
A, the length of its centre-line is L. The length of the
closing iron core is l and its cross-section is also
A. A current I flows through the coil surrounding the
U-shaped iron core; when the closing iron core is at distance h
from the U-shaped iron core, it is pulled by force F to the
electromagnet. (The permeability of iron is not constant, but its
dependence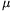 
(B) on the magnetic
induction is known.) a) How many turns does the coil consist
of? b) With what force does the electromagnet attract the
closing core when there is no air gap between them? What are then the
values of the magnetic induction and the relative permeability in the
iron? Data: L=30 cm, l=12 cm,
A=10 cm2,
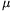h=1 mm, I=1 A, F=500 N, and (B)=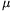0(4500-2500 T-1 B) in the investigated range.
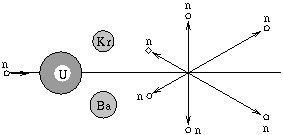P. 3342. The following
reaction may occur in the course of the fission of a 238U nucleus induced by a fast neutron:
.
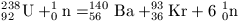Assume that the fission occurs as shown in the figure and the following are true: a) the kinetic energy of the incoming fast neutron is 3.2.10-13 J; b) the 6 neutrons produced in the course of the fission fly off in one plane, symmetrically to the direction of motion of the incoming neutron, at angles of 60o from each other; c) the nuclear energy released is 2.88.10-11 J; d) the kinetic energy of the neutrons flying off at right-angles and that of those flying "backwards" is identical: 1.6.10-13 J; e) the Kr and Ba nuclei produced in the course of the fission also fly off at right-angles. What are the separate kinetic energies of the produced nuclei?
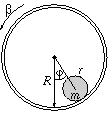P. 3343. A tube with
internal radius R and fixed axis is rotated with a small
angular acceleration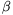 
. A solid rod
of homogeneous mass distribution with mass m and radius r
is placed inside the tube. (Friction is strong enough so that the
rod always rolls without sliding in the tube.) a) What should
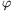the angle shown in the figure be
so that the axis of the rod remains at the same place? b) How
does the rod move if initially it is at the bottom of the tube?
Bonus Problem (April extra). Estimate how much longer a day would be if at midnight on 1 April 2000 everywhere in the world traffic started to keep to the right?