New exercises and problems in Mathematics
April 2000

Please read The Conditions of the Problem Solving Competition.

New exercises in April 2000

C. 580. Jane took several exams in math during the academic year, and once she did quite badly. When repeating the poor exam, the teacher offered that instead of the two grades, she can have the average of the two grades. Show that this is advantageous for Jane if and only if the average of all her other grades is better than the average of these two.

G. Kovács, Budapest

C. 581. Four vehicles start at the same time from A and arrive at B one after the other, at equal intervals. The speed of the fastest and the slowest vehicle is v₁ and v₄, respectively. Calculate the speed of the two other vehicles.

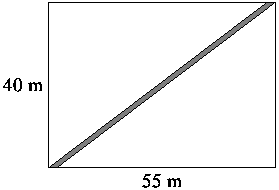
C. 582.  The strip depicted on the figure is 1m wide. Calculate its area.

Z. Nagy, Budapest

C. 583. The base of a pyramid is a unit square. One of its lateral edges is also of unit length, moreover, it coincides with the altitude of the pyramid. Calculate the largest dihedral angle of the pyramid.

M. Salát, Budapest

C. 584. The area or the perimeter of a circle can be better approximated (that is, with the smaller relative error) using a regular n-gon inscribed the circle?

New problems in April 2000

B. 3362. Eighteen students solved the problems proposed in the April issue of the KöMaL, one problem each. They plan to discuss their solutions via e-mail. At least how many e-mail messages have to be sent so that each student knows each solution in the end? (An e-mail message counts as many times as many recipients it is sent to.) (5 points)

B. 3363. Is there any triangle which can be dissected into three congruent parts by just two straight cuts? (3 points)

B. 3364. Assume that 15 different (positive) prime numbers are consecutive terms of an arithmetic progression. Prove that the common difference is larger than 30000. (3 points)

T. Székelyhidi, Budapest

B. 3365. Assume that abc=1 and 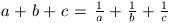. Prove that at least one of the numbers a, b, c equals 1. (3 points)

N. Gyanta, Budapest

B. 3366.  The grashopper of F. 3279. rides again. This time it is jumping to and fro between the points of a circle and a straight line which is not passing through the center of the circle. The length of each jump is r, the radius of the circle. Prove that there are at most 8 points for the grasshopper to reach. (5 points)

A. Hraskó, Budapest

B. 3367. An isosceles triangle shaped piece of paper is folded such that vertex A is moved onto the midpoint of leg BC. One endpoint of the folding edge divides leg AC into the ratio p:q. In what ratio does the other endpoint of the folding edge divide side AB? (5 points)

B. 3368. How many positive integer solutions does the equation x⁷+y⁸=z⁹ have? (4 points)

A. Behm, Nagykanizsa

B. 3369. On each edge of a tetrahedron, select one of the points that trisect the given edge. What can be the ratio between the volume of the convex polyhedron determined by these points and the volume of the tetrahedron?(4 points)

B. 3370. A and B are two events. Prove that |P(A^.B)-P(A)^.P(B)|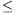1/4. (5 points)

B. 3371. Two ellipses have a common focus. How many common tangents can the ellipses have? (5 points)

New advanced problems in April 2000

A. 227. (Modified version of the problem proposed in January 2000.) Is there a positive integer n such that for every digit i, different from 0, i appears the same number of times in the decimal form of each of the numbers n, 2n, 3n, ..., 2000n?

A. 236. In a triangle of area t, let s_a, s_b and s_c denote the medians that correspond to sides a, b and c, respectively. Assume that a<b<c. Prove that 4acs_as_c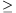16t²+(b²-a²)(c²-b²).

A. 237. Prove that among any kn+1 different diagonals of a convex n-gon there are 2k+1 which form an opened polygon that does not intersect itself.

A. 238. Let x be a positive real number and let k be a positive integer. Assume that x^k+1/x^k and x^k+1+1/x^k+1 are both rational numbers. Prove that x+1/x, is also a rational number.

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary

or by e-mail to: megoldas@komal.elte.hu.

Deadline: 15 May 1999