Matematikából kitűzött gyakorlatok és feladatok
2000. december

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 605. Oldjuk meg az alábbi egyenletet.

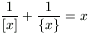
([x] az x szám egész részét és {x} a tört részét jelöli.)

C. 606. Az udvaron egy téglalap alakú részt egyforma négyzetlapokkal lebetonoztak. Pontosan 20 sort raktak le, s minden sorban 35 lap van. Egy csiga elindul a téglalap egyik csúcsából az átló mentén. Hány négyzetlap belsején halad át, mire a szemközti csúcsba ér?

C. 607. Egy 12 cm oldalú négyzetet a P pont körül 90^o-kal elforgatunk. A két négyzet együttesen 211 cm² területet fed le. Az elforgatott négyzetet a P körül ismét elforgatjuk 90^o-kal, így egy harmadik négyzetet kapunk. A három négyzet által lefedett terület 287 cm². Határozzuk meg a P pont helyzetét.

Javasolta: Bakonyi Gábor, Budapest

C. 608. Mekkora annak a valószínűsége, hogy egy KENO sorsolás alkalmával az 1-től 80-ig terjedő egész számok közül kisorsolt 20 szám egyikében sem fordul elő a 8-as számjegy?

C. 609. Bizonyítsuk be, hogy a 3x-4y+4=0 egyenletű egyenes a sík bármely rácspontjától racionális távolságra van.

A B pontversenyben kitűzött feladatok

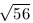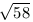B. 3412. Mutassuk meg, hogy két kivétellel minden pozitív egész q számhoz létezik olyan p egész, hogy <p/q<. (3 pont)

Az NRICH Online Maths Club feladata

B. 3413. A tavaly még professzionálisnak nevezett magyar labdarúgó bajnokság egy csoportjában az idén 8 csapat szerepel. Minden meccs egyik résztvevője otthon, a másik idegenben játszik. Egy idényben, amikor minden csapat minden másikkal pontosan egyszer játszik, egy csapat sorsolását igazságosnak nevezzük, ha felváltva játszik otthon és idegenben. Lehet-e olyan sorsolást készíteni, amelyben mind a 8 csapat sorsolása igazságos? (4 pont)

B. 3414. Egy húrnégyszög átlói merőlegesek egymásra, oldalhosszai négyzetének összege 8 egység. Határozzuk meg a körülírt körének sugarát. (3 pont)

Javasolta: Besenyei Ádám, Tatabánya

B. 3415. A p paraméter mely értékeire van az

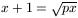
egyenletnek pontosan egy valós gyöke? (4 pont)

B. 3416. Egy négyszöglapokkal határolt konvex poliéder felszíne A, éleinek négyzetösszege Q. Bizonyítsuk be, hogy Q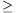2A. (4 pont)

Javasolta: Besenyei Ádám, Tatabánya

B. 3417. Tekintsük a síkon az összes olyan kört, amelynek egyenlete felírható

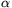 ((x-2)²+y²-1)+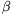((x+2)²+y²-1)=0

alakban, ahol 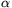és 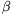valós számok. Hol vannak azok a pontok, amelyek egyik ilyen körön sincsenek rajta? (4 pont)

B. 3418. Az ABC háromszögben az A, B, illetve C csúcsokból induló súlyvonalak a háromszög köré írt kört rendre az A₁, B₁, illetve C₁ pontokban metszik. Bizonyítsuk be, hogy t_A1BC+t_B1CA+t_C1AB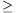t_ABC. (5 pont)

Javasolta: Varga István, Békéscsaba

B. 3419. A sík mely pontjaiból húzható az y=x³ egyenletű görbéhez három érintő? (4 pont)

B. 3420. Keressünk olyan f:R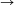R nem konstans függvényt, amelynek grafikonja 3-szoros nagyítással kapható a függvény négyzetének grafikonjából. (5 pont)

Javasolta: Lóczi Lajos, Budapest

B. 3421. Bizonyítsuk be, hogy ha x, y, u és v olyan egész számok, amelyekre (x²+3y²)/(u²+3v²) egész, akkor alkalmas a, b egészekkel ez a hányados is felírható a²+3b² alakban. (5 pont)

Javasolta: Csörnyei Marianna, London

A megoldáshoz ajánljuk az 513. oldalon kezdődő, Számelmélet az x²+dy² alakú számok körében című cikk elolvasását.

A pontversenyben kitűzött nehezebb feladatok

A. 251. Adott a térben egy gömb. Ha a P pont illeszkedik a gömbre, a Q pont pedig nem, akkor jelölje P_Q a PQ egyenes és a gömb P-től különböző metszéspontját. Ha a PQ egyenes érinti a gömböt, akkor legyen P_Q=P.

Igazoljuk, hogy ha a gömb A, B, C, D pontjai nincsenek egy síkban, akkor legfeljebb két olyan Q pont létezik, amelyre az A_QB_QC_QD_Q tetraéder egyenlő oldalú. (Egy tetraédert egyenlő oldalúnak nevezünk, ha a lapjai egybevágóak.)

A. 252. Igazoljuk, hogy ha az a₁,...,a_n egész számok (n+k)-val osztva összesen legalább k+1 különböző maradékot adnak, akkor kiválasztható közülük néhány (lehet, hogy csak egy; lehet, hogy az összes), amelyek összege osztható (n+k)-val.

Javasolta: Károlyi Gyula és Podoski Károly, Budapest

A. 253. Keressük meg az összes olyan f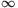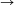:(0,)(0,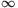) függvényt, amelyre tetszőleges x, y pozitív valós számok esetén

f(x)f(yf(x))=f(x+y).

IMC 2000, London

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. január 15.