New exercises and problems in Mathematics
February
2001
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in February 2001 |
C. 615. A piece of music is composed of three movements; its total playing time is 60 minutes. No movement is any longer then the other two altogether. The difference between the playing times of any two movements is at least 3 minutes. Determine the range for the playing time of the shortest movement.
C. 616. Eight people are travelling together in a railway compartment. Is it possible that the respective numbers of acquaintances in the compartment are
a) 1, 3, 3, 4, 5, 6, 6, 6;
b) 1, 3, 3, 4, 5, 6, 6, 7?
C. 617. The midpoint of the base AB of the isosceles triangle ABC is denoted by D. Let P denote the foot of the perpendicular dropped from D to CB and F the midpoint of segment DP. Express the area of the quadrilateral AFPC in terms of the length of CF and AP.
C. 618. Take any rectangle ABCD such that AB>BC. The point P is on AB and Q is on CD. Show that there is exactly one position of P and Q such that APCQ is a rhombus. Show also that, by choosing a suitable rectangle, the ratio of the area of the rhombus to the area of the rectangle can take any value strictly between 1/2 and 1.
C. 619. Determine the number of such integers n, lying between 1 and 100000 so that n3+23n is a multiple of 24.
 |
New problems in February 2001 |
B. 3432. The array below is constructed in a similar way as Pascal's triangle. The first row in the array contains the numbers 1 and 2, every further entry is the sum of the two neighbours above.
| 1 | 2 | |||||||
| 1 | 3 | 2 | ||||||
| 1 | 4 | 5 | 2 | |||||
| 1 | 5 | 9 | 7 | 2 | ||||
a) Determine the sum of the entries in the 100th row.
b) What do we get if the entries in the 100th row are summed with alternating signs?
c) Determine the 47th element in the 100th row. (4 points)
B. 3433. The participants of a geometry conference got curious sandwiches with the refreshments. On the top of each cuboid-shaped slice of bread there was a thick slice of cheese in the shape of a cylinder and also a spherical meat ball. Is it always possible to cut such a sandwich into two parts with a straight cut such that the two parts contain the same amount of each ingredient? (4 points)
B. 3434. A trapezium has bases a and b. A line parallel to its bases cuts the trapezium into two parts such that a circle can be inscribed into each sub-trapezium. Determine the perimeter of the original trapezium. (3 points)
B. 3435. Find all non-negative solutions of the following system of equations:
x1+x2+x3+...+x100=5050,
x22-x12=3, ..., xk2-xk-12=2k-1, ... x1002-x992=199.
(4 points)
B. 3436. Triangle ABC has a unit area. Points A1, B1 and C1 lie on the sides BC, CA and AB, respectively, such that AC1/C1B=1/2, BA1/A1C=1/3, CB1/B1A=1/4. Determine the area of the triangle enclosed by the lines AA1, BB1 and CC1. (3 points)
B. 3437. Points A, B, C, D are, in this order, incident to a line such that BC=2AB and CD=AC. Draw two circles; one passing through points A and C, the other incident to B and D. Prove that the common chord of the two circles halves the segment AC. (4 points)
B. 3438. The function f(x,y,z) satisfy the equations
f(x+t,y+t,z+t)=t+f(x,y,z)
f(tx,ty,tz)=tf(x,y,z)
f(x,y,z)=f(y,x,z)=f(x,z,y)
for every real number t. Determine the value of f(2000, 2001, 2002). (5 points)
B. 3439. Consider the infinite sequence 1, p, 1\over p, p2, 1/p2, ..., pn, 1/pn, ..., where p is a positive number. Find those values of p for which every positive number can be arbitrarily closely approximated with a finite sum of suitable elements of the above sequence. (5 points)
B. 3440. Points A1, B1,
C1 and A2, B2,
C2 are obtained by reflecting the points
A, B, C in a line e and in a point P,
respectively. Assume that 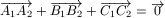 . What is the
mirror image of P through e? (3 points)
. What is the
mirror image of P through e? (3 points)
B. 3441. Pinocchio has to pass 9 obstacles before he can turn into a real boy. It is not easy: any time he fails he has to go back to the previous obstacle he just passed and try it once more. If he ever fails at the first obstacle he will remain a wooden doll forever. Stubborn Pinocchio does not learn from his failures: the probability of success at the given obstacles is always the same, namely 1/10, 2/10, ..., 9/10 respectively, no matter how many times had he tried them before. How should The Fairy With The Blue Hair arrange the obstacles to maximize the probability that Pinocchio turns into a real boy? What is this probability? (5 points)
 |
New advanced problems in February 2001 |
A. 257. n marbles are to be measured with the help of a one-armed balance. We are allowed to measure one or two marbles at a time. It may happen, however, that one of the results is misread. Denote by f(n) the minimum number of weighings necessary to determine the weight of each marble. Prove that f(n)>n+log 3n-3.
Based on a problem proposed by L. Surányi and B. Virág
A. 258. Six points, A, B,
C, D, E and F are on a line e such that 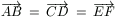 . Given a ruler, construct a line parallel to
e.
. Given a ruler, construct a line parallel to
e.
A. 259. Suppose that u>1 and the positive numbers x1, x2, ..., xn and y1<y2<...<yn satisfy the inequality
x1u+x2u+...+xku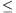 y1u+y2u+...+yku
y1u+y2u+...+yku
for every 1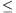 k
k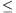 n. Prove that
n. Prove that
x1+x2+...+xn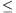 y1+y2+...yn.
y1+y2+...yn.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.

