A 2001. márciusi B-jelű matematika gyakorlatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B.3442. Van-e olyan 2001 jegyű természetes szám, amely - a tízes számrendszerben felírva - megegyezik a 2001-edik hatványának utolsó 2001 számjegyével? (4 pont)
Javasolta: Kiss Tamás, Budapest
Megoldás.
Ha egy a szám négyzete ,,a-ra végződik'', akkor minden további hatványa is; elegendő tehát olyan 2001 jegyű a számot találni, amelyre 102001|a2-a=a(a-1). Utóbbi biztosan teljesül, ha 22001|a és 52001|a-1, és akkor is, ha 52001|a és 22001|a-1. Az első két oszthatósági feltételt kielégítő számot keressük a=22001x alakban (ekkor az első oszthatóság már biztosított), erre még 22001x-1=52001y-nak, azaz 22001x-52001y=1-nek kell teljesülnie. Mivel 22001 relatív prím 52001-hez, ilyen x (és y) egész biztosan létezik, és az ezzel képezett 22001x szám 102001-nel való a1 osztási maradéka egy, a feladat feltételét kielégítő legfeljebb 2001 jegyű szám. Hasonlóan kaphatunk olyan, ugyancsak legfeljebb 2001 jegyű a2 számot, amelyre 52001|a2 és 22001|a2-1. Mivel 22001|a1, 52001|a2, 52001|a1-1, 22001|a2-1, azért a1a2=102001c és (a1-1)(a2-1)=102001d, alkalmas c>d pozitív egészekkel. Így a1+a2-1=a1a2-(a1-1)(a2-1)=102001(c-d) is osztható 102001-nel, ezért legalább 102001. Tehát az a1 és a2 közül legalább az egyik 2001 jegyű, ellenkező esetben ugyanis \(\displaystyle 10^{2001}\leq a_1+a_2-1 B.3443.
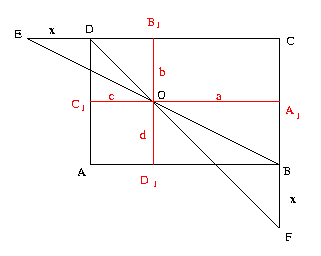
Az ABCD téglalap CB oldalának
B-n túli meghosszabbítására, valamint a CD oldalának D-n
túli meghosszabbítására egyenlő hosszúságú szakaszokat mértünk fel. Így kaptuk
az F, illetve az E pontokat. Igazoljuk, hogy az EB és az
FD egyenesek metszéspontját A-val összekötő egyenes felezi az
A csúcsnál lévő szöget. (3 pont)
Megoldás.
\(\displaystyle OB_1E\triangle\sim
BA_1O\triangle\),
így \(\displaystyle {b\over{x+c}}={d\over a}\), amiből
ab=d(x+c). \(\displaystyle FA_1O\triangle\sim OB_1D\triangle\), így \(\displaystyle {b\over c}={{d+x}\over a}\), amiből ab=(d+x)c. Ebből következik, hogy d(x+c)=(d+x)c, tehát dx=cx, és mivel \(\displaystyle x\neq0\), ezért c=d. Így az AD1OC1 négyszög négyzet, így átlója, OA, felezi az A csúcsnál levő szöget.
B.3444.
A pozitív egész számokból álló végtelen
a1, a2, a3, ...
an, ... sorozatban jelölje
fn az n természetes szám előfordulásainak a
számát, ha ez az érték véges.
Az a1, a2, ...
an, ... sorozat ,,gyakoriságsorozata'' ezután az
f1, f2, ... fn,
... sorozat, ha minden fi véges. Hasonlóan
értelmezzük a fenti f1, f2, ...
fn, ... sorozat gyakoriságsorozataként az
a1, a2, ...
an, ... sorozat másodrendű gyakoriságsorozatát, ha
minden gyakoriság véges, és ennek gyakoriságsorozataként a harmadrendű
gyakoriságsorozatot és így tovább.
Van-e olyan a1, a2,
... an, ... sorozat, amelynek minden k-ra
létezik a k-adrendű gyakoriságsorozata? (4 pont)
Megoldás.
Igen, van ilyen sorozat. Az alábbi, ,,Öndokumentáló'' sorozat önmaga gyakoriságsorozata is egyben és így persze minden k-ra létezik k-adrendű gyakoriságsorozata: önmaga.
Legyen a1=1, a2=2=a3. Ezután a3 értéke szerint írjunk 2 darab 3-ast, így a4=3, tehát most 3 darab 4-est kell írnunk, és így tovább. Szemléletesen világos, hogyan épül fel a sorozat és hogy a konstrukció akadály nélkül folytatható, az alábbiakban ennek precíz bizonyítását adjuk. Ehhez az an sorozattal együtt egy mk sorozatot is definiálunk: ezek azok a helyek, ahol az an sorozat ,,ugrik'', mk értéke az a legkisebb sorszám, ahol az an sorozat értéke k.
Legyen m1=a1=1. Legyen most n>1 és tegyük fel, hogy az mk sorozat értékeit már definiáltuk, ha \(\displaystyle 1\leq k Az indukciós feltevés szerint \(\displaystyle n-1\leq m_{n-1}\) és így an-1 értéke is definiált. Legyen most mn=mn-1+an-1, ai=n-1, ha mn-1<i<mn, végül legyen amn=n. Mivel az indukciós feltevés szerint \(\displaystyle n-1\leq m_{n-1}\) másrészt nyilván \(\displaystyle 1\leq a_{n-1}\), azért \(\displaystyle n\leq m_n\) továbbra is fennáll.
Végül a sorozat készítése alapján nyilvánvaló, hogy ha \(\displaystyle n\geq1\), akkor az n érték pontosan mn+1-mn=an-szer fordul elő a sorozatban, tehát fn=an minden n-re.
B.3445.
Van-e olyan háromszög, amelyet valamelyik
oldalával párhuzamosan ketté lehet vágni úgy, hogy a két rész kerülete is és
területe is egyenlő? (4 pont)
Javasolta: Reményi Gusztáv, Budapest
Megoldás.
Bármely háromszög felosztható az egyik oldalával párhuzamos egyenessel két egyenlő területű részre: mivel az így kapott kis háromszög és a hozzá hasonló nagy háromszög területének aránya 1:2, oldalaik aránya 1:\(\displaystyle \sqrt2\). Ahhoz, hogy az a, b, c oldalú háromszög szétvágásakor a kerületek is egyenlőek legyenek, annak kell teljesülnie, hogy
\(\displaystyle {1\over{\sqrt2}}a+{1\over{\sqrt2}}b+{1\over{\sqrt2}}c={1\over{\sqrt2}}b+\left(1-{1\over{\sqrt2}}\right)a+b+\left(1-{1\over{\sqrt2}}\right)c,\)
ahonnan \(\displaystyle (\sqrt2-1)(a+c)=b\). Olyan háromszög, amelynek oldalaira ez az egyenlőség teljesül, végtelen sok van, például a=1, b=1, \(\displaystyle c=\sqrt2\) esetén az egyenlő szárú egység befogójú derékszögű háromszög.
B.3446.
Határozzuk meg a q(x) polinomot úgy,
hogy a p(x)=x2+x+1 polinommal
p2(x)-2p(x)q(x)+q2(x)-4p(x)+3q(x)+3 Megoldás.
Ilyen a \(\displaystyle q_1=x^2+2x-\frac{1}{2}\) és a \(\displaystyle q_2=x^2-\frac{3}{2}\) polinom. Ezeket a q-ra nézve másodfokú q2-(2p-3)q+(p2-4p+3)\(\displaystyle equiv\)0 egyenlet megoldásaiként kaphatjuk meg. Ha végiggondoljuk a másodfokú egyenlet megoldóképletének a levezetését és figyelembe vesszük azt a tényt, hogy nemnulla polinomok szorzata sosem a nullapolinom, akkor könnyen beláthatjuk, hogy az említett két polinomon túl nincs a feladatnak több megoldása.
B.3448.
Mutassuk meg, hogy adott ellipszisbe írt olyan
háromszögek területe, amelyek súlypontja egybeesik az ellipszis középpontjával,
állandó. (4 pont)
Javasolta: Kiss Sándor, Szatmárnémeti
I. Megoldás.
Legyen az ellipszis egyenlete ax2+by2=1 (a,b>0). A háromszög csúcsainak koordinátáit jelölje (x1,y1), (x2,y2), (x3,y3). A súlypontra vonatkozó feltétel x1+x2+x3=y1+y2+y3=0 alakban írható fel. A háromszög területének kétszerese 2T=|x2y3-y2x3+x3y1-y3x1+x1y2-y1x2|=3.|x1y2-x2y1| az x3=-x1-x2, y3=-x1-x2 feltétel miatt. Ezért \(\displaystyle \left({{2T}\over3}\right)^2=x_1^2y_2^2+x_2^2y_1^2-2x_1x_2y_1y_2\). Az ax12+by12=ax22+by22=a(x1+x2)2+b(y1+y2)2=1 feltételekből 2ax1x2+2by1y2=-1 is adódik, ezt a fenti képletbe kétféleképpen behelyettesítve \(\displaystyle a\left({{2T}\over3}\right)^2=y_2^2(1-by_1^2)+y_1^2(1-by_2^2)-y_1y_2(-1-2by_1y_2)=y_1^2+y_2^2+y_1y_2={1\over2}(y_1^2+y_2^2+y_3^2)\) és \(\displaystyle b\left({{2T}\over3}\right)^2={1\over2}(x_1^2+x_2^2+x_3^2)\) adódik. Az elsőt b-vel, a másodikat a-val szorozva \(\displaystyle 2ab\left({{2T}\over3}\right)^2={1\over2}(ax_1^2+by_1^2+ax_2^2+by_2^2+ax_3^2+by_3^2)=3/2,\) vagyis \(\displaystyle T={{3\sqrt3}\over{4\sqrt{ab}}}\) csak az ellipszistől függő állandó.
II. Megoldás.
Jelölje az ellipszis kis- és nagytengelyének hosszát 2A, illetve 2B, ekkor az ellipszis előáll egy A sugarú körhengernek az alapkör síkjával $ szöget bezáró síkkal való metszeteként. Vetítsük a háromszöget az alapkör síkjára. A vetület súlypontja éppen az alapkör középpontja, ez egyszerű vektoros megfontolásból látszik ha az alapkör középpontjából a csúcsokba mutatóvekktorokat felbontjuk az alapkör síkjával párhuzamos ill. arra merőleges összetevőkre, hiszen az ellipszis középpontjának merőleges vetülete éppen az alapkör középpontja. Ezért a vetület minden esetben az alapkörbe írt szabályos háromszög, hiszen minden súlyvonala egybeesik a megfelelő oldalfelező merőlegessel, és ennek következtében bármely két oldal egyenlő hosszúságú. A vetület területe tehát független az eredeti háromszögtől, csak magától az ellipszistől függ. Másrészt azonban a vetület terület éppen az eredeti háromszög területének \(\displaystyle \cos\varphi={A\over B}\)-szerese, ami könnyen igazolható ha a háromszöget és vetületét is felbontjuk egy-egy az ellipszis és az alapkör síkjának metszésvonalával párhuzamos egyenessel két-két kisebb háromszögre, melyek alapja megegyezik, és a vetület háromszögek magassága pedig a megfelelő háromszögek magasságának éppen cos\(\displaystyle varphi\)-szerese. Ezért az eredeti háromszög területe is állandó, mégpedig \(\displaystyle {{3\sqrt3}\over4}AB\)-vel egyenlő.
B.3449.
Legyen a>1 adott egész szám. Bizonyítsuk
be, hogy ha az x2-ay2=-1 egyenletnek van
egész megoldása, akkor végtelen sok egész megoldása van. (5 pont)
Javasolta: Fried Ervin, Budapest
Megoldás.
Világos, hogy a nem lehet teljes négyzet, hiszen két olyan négyzetszám különbsége nem lehet 1, ahol legalább az egyikük 1-nél nagyobb. Így \(\displaystyle \sqrt{a}\) irracionális. Feltehető, hogy a létező (x0,y0) megoldásban x0,y0>0 (x=0 nyilván lehetetlen). Legyen \(\displaystyle \beta=x_0+\sqrt{a}y_0\); ekkor \(\displaystyle beta\)>1, és \(\displaystyle beta\) hatványai (amelyek páronként különbözők) \(\displaystyle x+\sqrt{a}y\) alakúak. Minden páratlan kitevőhöz tartoző x,y-ra x2-ay2=-1 teljesül. (További részletek találhatók az áprilisi B. 3461. feladat megoldásában. )
B.3450.
Tekintsük azokat a síkokat, amelyek a T
tetraéder lapsíkjaival párhuzamosak, és a T-ből általuk levágott kis
tetraéderek térfogata T térfogatának 1/3 része. A T térfogatának
hányadrésze marad meg, ha csúcsait levágjuk ezekkel a síkokkal? (5 pont)
Megoldás.
A metszősíkok és az eredeti tetraéder
lapsíkjai három típusú kis tetraédert határoznak meg, amelyek a síkok
párhuzamossága miatt mind hasonlók lesznek az eredeti Az eredeti tetraéder mind a 4 csúcsánál egy-egy olyan tetraéder keletkezik, amely éleinek hossza A megmaradó test térfogata ezek alapján (ha 1-4.a3+6.(2a-1)3-4.(3a-2)3\(\displaystyle approx\)0,01163.
Tehát a
B.3451.
Oldjuk meg a következő egyenletet: Megoldás.
Legyen
 0 azonosság teljesüljön. (4 pont)
0 azonosság teljesüljön. (4 pont)
 tetraéderhez. Hasonló testek térfogatának aránya a hasonlóság arányának a köbével egyezik meg. Legyen a3=1/3.
tetraéderhez. Hasonló testek térfogatának aránya a hasonlóság arányának a köbével egyezik meg. Legyen a3=1/3.
 megfelelő élei hosszának a-szorosa.
megfelelő élei hosszának a-szorosa.  mind a 6 élénél egy-egy olyan tetraéder keletkezik, amely éleinek hossza
mind a 6 élénél egy-egy olyan tetraéder keletkezik, amely éleinek hossza 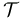 megfelelő élei hosszának (2a-1)-szerese, végül pedig
megfelelő élei hosszának (2a-1)-szerese, végül pedig 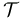 mind a négy lapjánál egy-egy olyan tetraéder keletkezik, amely éleinek hossza
mind a négy lapjánál egy-egy olyan tetraéder keletkezik, amely éleinek hossza 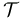 megfelelő élei hosszának (3a-2)-szorosa (lásd az ábrát).
megfelelő élei hosszának (3a-2)-szorosa (lásd az ábrát).
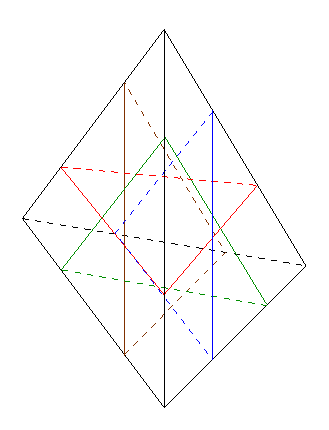
 térfgata 1 egység):
térfgata 1 egység):
 térfogatának 1163 tízezrede marad meg.
térfogatának 1163 tízezrede marad meg.
 . (4 pont)
. (4 pont)
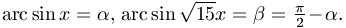 Ekkor sin\(\displaystyle alpha\)=x és \(\displaystyle \cos\alpha=\sin({{\pi}\over2}-\alpha)=\sin\beta=\sqrt{15}x\). A
trigonometrikus Pithagorasz-tételből \(\displaystyle x^2+(\sqrt{15}x)^2=1\),
Ekkor sin\(\displaystyle alpha\)=x és \(\displaystyle \cos\alpha=\sin({{\pi}\over2}-\alpha)=\sin\beta=\sqrt{15}x\). A
trigonometrikus Pithagorasz-tételből \(\displaystyle x^2+(\sqrt{15}x)^2=1\), 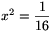 ,
, 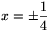 adódik. Az
\(\displaystyle x={1\over4}\) esetben
valóban
adódik. Az
\(\displaystyle x={1\over4}\) esetben
valóban
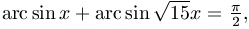 , mint ahogyan az a fenti gondolatmenet
megfordításával könnyen ellenőrizhető. Hasonlóan,
, mint ahogyan az a fenti gondolatmenet
megfordításával könnyen ellenőrizhető. Hasonlóan, 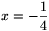 esetén
esetén
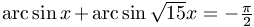 , ez tehát nem megoldása a feladatnak. Az egyenlet megoldása tehát \(\displaystyle x={1\over4}\).
, ez tehát nem megoldása a feladatnak. Az egyenlet megoldása tehát \(\displaystyle x={1\over4}\).

