New exercises and problems in Mathematics
March
2001
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in March 2001 |
C. 620. A trapezium is called symmetrical if the perpendicular bisectors of its bases coincide. Is it true that every trapezium which has a symmetry is symmetrical?
C. 621. The baker prepares raisin bread. How many raisins should he add to the dough in order to ensure that every 40 gram slice of the 1 kilogram loaf will contain a raisin with a probability at least 0.99?
C. 622. Find all 6-digit number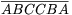s 
, divisible by
7, for which \(\displaystyle \overline{ABC}\) is also divisible by 7. (Here A, B and
C denote different digits.)
C. 623. Solve the system of the following equations: a2b2-a2-ab+1=0, a2c-ab-a-c=0, abc=-1.
Proposed by S. Kiss, Szatmárnémeti
C. 624. The diameter of a standard table tennis ball is 4 cm. Is it possible to pack 100000 such balls in a box whose dimensions are 200 cm, 164 cm and 146 cm?
 |
New problems in March 2001 |
B. 3442. Is there any 2001-digit number that can be obtained as the last 2001 digits of its 2001st power? (4 points)
Proposed by: T. Kiss, Budapest
B. 3443. The sides CB and CD of a rectangle ABCD are extended beyond B and D, respectively, and points F and E are produced on these lines such that BF=DE. Prove that the line connecting A with the intersection point of lines EB and FD halves the angle at vertex A. (3 points)
B. 3444. In a sequence a1, a2, ... of positive integers, let fn denote the number of times the positive integer n occurs in the sequence, provided that this number is finite. If fn is finite for every n, then the sequence f1, f2, ... is called the frequency sequence of a1, a2, .... If the sequence f1, f2, ... also admits a frequency sequence, it is then called the 2nd frequency sequence of the sequence a1, a2, .... Frequency sequences of higher order are defined similarly. Is there any sequence which admits a kth frequency sequence for every positive integer k? (4 points)
B. 3445. Is there any triangle which can be dissected into two parts by a line parallel to one of its sides such that the two parts have equal area and also equal perimeter? (4 points)
JavasoltaProposedBy: G. Reményi, Budapest
B. 3446. Let p(x)=x2+x+1. Determine the polynomial q(x) such that p2(x)-2p(x)q(x)+q2(x)-4p(x)+3q(x)+3 is identically 0. (4 points)
B. 3447. Each side of triangle ABC is extended, in clockwise direction, to twice its length. Next, each side of the triangle A1B1C1 thus obtained is extended, this time in counter-clockwise direction, to twice its length, yielding triangle A2B2C2. Prove that this triangle is similar to triangle ABC. Find a similar statement for quadrilaterals. (4 points)
B. 3448. Inscribe a triangle in a given ellipse such that its centroid coincides with the centre of the ellipse. Prove that the area of the triangle is independent of the position of the triangle. (4 points)
Proposed by: S. Kiss, Szatmárnémeti
B. 3449. Let a>1 be an integer such that the Diophantine equation x2-ay2=-1 has a solution. Prove that it has an infinite number of solutions. (5 points)
Proposed by: E. Fried, Budapest
B. 3450. Given a tetrahedron T, consider those planes parallel to the faces of T which cut off 1/3 the volume of T. What proportion of the volume of T remains after chopping off each vertex of T with these planes? (5 points)
B. 3451. Solve the equation \(\displaystyle \arcsin x+\arcsin\sqrt{15}x=\pi/2\). (4 points)
 |
New advanced problems in March 2001 |
A. 260. Four points, A, B, C and D, are given on a line e such that \(\displaystyle \overrightarrow{AB}=\overrightarrow{CD}\). Is it possible to construct a line parallel to e with the help of a single ruler?
A. 261. Alice and Bob assemble equilateral triangles of unit side to form an equilateral triangle of side n. They play the following game on the triangular grid thus obtained. They move alternately, Alice moving first. At each move they colour one grid point red, blue or green. When every point is coloured, they count those triangles of unit side whose vertices have three different colours. Alice gets a score for each of those triangles whose red, blue and green vertices are in clockwise order, while Bob gets a score for each red-blue-green triangle oriented counter-clockwise. The one who has the higher score, wins. Which player has a winning strategy?
A. 262. Let 0<a<b<c be positive integers. Prove that there exist integers x, y and z, not all 0, such that ax+by+cz=0, and |x|, |y|, |z| are all less than \(\displaystyle {2\over{\sqrt3}}\sqrt c\).
Based on a problem of the 2000 Schweitzer Competition
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.