 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 225. Let a drop of oil fall into pure water. Measure how the ``penetration depth'' depends on the dropping height and on the size of the drop. (6 points)
New problems:
P. 3437. A wooden disc with a thickness of 2 cm and a density of 0.5 kg/dm3 is floating on water.
a) What is the maximum thickness of an aluminium disc of the same area that, when placed onto the wooden disc, the latter does not disappear completely under the water.
b) What is the answer when the aluminium disc is fastened onto the bottom of the wooden disc? (3 points)
P. 3438. An alloy is made of copper and nickel at a proportion of 1:1. What is the density of this alloy if the two metals mix without change in their respective volumes? (4 points)
P. 3439. Two bodies with a mass of 1 kg each hang on a spring with a directional force of 200 N/m, attached to each other using a thread with a length of 10 cm, as shown in the figure. We burn the thread. What is the distance between the two bodies when the top body first arrives at its highest position?
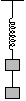
(4 points)
P. 3440. One side of a pull-push spring of initial, unstretched length l0, lying on an air-cushioned table, is fixed, the other one is fastened to a small puck of mass m. The puck is thrust in a direction perpendicular to the spring, at an initial speed v0. In the course of the motion, the maximum elongation of the spring is \(\displaystyle Delta\)l=l0/10. What is the force constant of the spring? Sketch the trajectory of the centre of the puck.
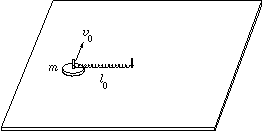
(5 points)
P. 3441. Some quantity of monatomic ideal gas can reach state B from state A (see the figure) following two different processes: AB or ACB. The heat taken up by the gas during process ACB is only 90 % of that taken up during process AB. Initially (in state A) the temperature of the gas is 150 K. What are the respective temperatures of the gas in states C and B?
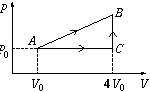
(5 points)
P. 3442. The mirror of length \(\displaystyle 2\,\ell\) makes 10 revolutions per minute about the axis crossing its midpoint O and perpendicular to the plane of the figure. There are a light source in point A and an observer in point B of the circle of radius R drawn around centre O (AOB\(\displaystyle angle\)=90o).
a) Along what curve does the virtual image of the point-like light source A move?
b) At what speed does the virtual image of A move?
c) What is the proportion \(\displaystyle R/\ell\) if the observer B first sees the light source when the angle of the mirror is \(\displaystyle phi\)=15o?
d) How long can the observer continuously see the light source in the mirror at such a proportion \(\displaystyle R/\ell\)?
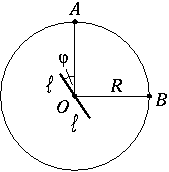
(5 points)
P. 3443. An electron with a kinetic energy of 100 eV enters the space between the plates of a plane capacitor made of two dense metal grids at an angle of 30o with the plates of the capacitor, and leaves this space at an angle of 45o with the plates. What is the pd. of the capacitor and at what kinetic energy does the electron leave the capacitor?
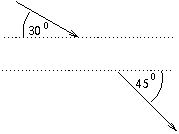
(4 points)
P. 3444. The equation of a "super-ellipse" is (x/a)4+(y/b)4=1, where a and b are the semi-axes. A homogeneous cylinder with a super-elliptical cross-section is placed onto a horizontal table with its long semi-axis in the vertical direction. Determine (using numerical, graphical or analytical methods) the maximum angle of deviation \(\displaystyle phi\) until which the position shown in the figure is stable. Represent \(\displaystyle phi\) as a function of the oblateness b/a.
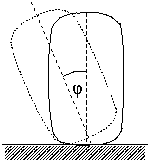
(6 points)
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.

