 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 7. The function Factorial(N)
increases very rapidly. While 5!=120, 4-byte integers are needed for
storing 10!=3 628 800. 100! can be handled by special softwares
only. We know however, that every natural number has its prime
factorization. For example 5!=23.3.5,
or
10!=28.34.52.7.
Your program should read the number N (1
N10 000) from the
keyboard, then print the prime factorization of its factorial
N! (10 points)
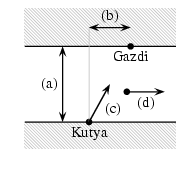
I. 8. A dog swims across the river, always heading for its trainer standing on the opposite riverside. The approximate path of the dog in the river is to be modelled and displayed on the screen. One should be able to input the following real parameters from the keyboard:
a) the width of the river in meters
b) the distance (in meters) of the trainer from the starting position of the dog projected onto the opposite riverside. (The distance is positive if it is in the same direction as the streamline of the river and negative otherwise.)
c) the constant magnitude of the velocity of the dog (in m/s)
d) the constant velocity of the river (in m/s)
e) the accuracy of approximation, that is the length of the time interval (in seconds) in which your program replaces the actual motion by a straight line segment. (See fig. on page 490.)
The two riversides are considered as parallel lines. Simulation should stop when the dog has approached the opposite riverside within 1 meter.
Draw the two sides of the river as parallel lines, the starting position of the dog and the trainer, and the path of the dog. (10 points)
I. 9. Binomial coefficients can be arranged
in the usual Pascal's triangle pattern (see fig. on page 490). Except
for the outermost entries in each row, every number is the sum of its
upper and upper-left neighbours. Prepare an Excel sheet capable of
displaying the first N+1 rows of Pascal's triangle in this
arrangement. Let the value of N (1N20) be entered in the 7th cell of
the first row. The sheet should contain exactly N+1 rows in
each case. (10 points)
| |||||||||||||||||||||||||||||||||||||||||||||||||