A 2002 áprilisi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 290. Adott véges sok négyzet alakú papírlap, amelyek területének összege 4 egység. Bizonyítsuk be, hogy lefedhető velük egy egységnyi négyzet.

Allan Wilson, Anglia

Megoldás. Csökkentsük a papírlapok méretét úgy, hogy továbbra is négyzet alakúak maradjanak, de az oldalhosszuk 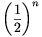alakú legyen. Ezt megtehetjük úgy, hogy a területük nem csökken az eredeti terület negyedénél kisebbre. Ezért az eredményül kapott négyzetek területének összege legalább 1 egység.

Ezután ismételgessük a következő műveletet, amíg lehetséges: ha van négy egyforma méretű négyzet, akkor ezeket illesszük össze egy kétszer akkora négyzetté. Mivel csak véges sok papírlap volt, ez az eljárás véges sok lépés után véget ér.

Az eljárás végén tetszőleges k egész számra legfeljebb 3 darab 1/2^k oldalú, 1/4^k területű négyzetünk van. Ezért az egységnyinél kisebb négyzetek területének összege kisebb, mint \(\displaystyle \sum_{k=1}^\infty3\cdot\left({1\over4}\right)^k=1\). Az egységnyinél kisebb négyzetek területének összege tehát nem adhatja ki az összes négyzet területének összegét. Ez azt jelenti, hogy az eljárás végén biztosan lesz legalább egységnyi oldalú négyzet is.

A. 291. Oldjuk meg az

\(\displaystyle x=\sqrt{2+\sqrt{2-\sqrt{2+x}}}\)

egyenletet.

Megoldás. A [-2,2] intervallumon kívül 2+x és 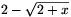valamelyike negatív, és emiatt a jobboldal nem értelmes. Ezért megoldást csak a [-2,2] intervallumban kereshetünk.

Legyen 0\(\displaystyle le\)t\(\displaystyle le\) az a szám, amelyre x=2cost. Ekkor

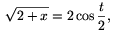
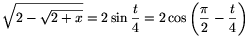
és

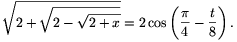
Az egyenlet tehát:

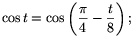
ebből 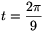és x=2cos40^o1,5321.

A. 292. Egy világvárosban n metróvonal van (n>4). Egy állomáson legfeljebb három metróvonal találkozik, és bármelyik két különböző metróvonalhoz létezik egy harmadik, amelyikre mindkettőről át lehet szállni. Igazoljuk, hogy a városban legalább 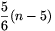metróállomás van.

Megoldás. Feltételezzük, hogy minden metróvonalon legalább két állomás van.

Vizsgáljuk először azt az esetet, ha minden vonalon legalább három állomás van. Számoljuk össze kétféleképpen az egymásra illeszkedő vonal-állomás párokat. A metróvonalak száma n, mindegyiknek legalább három állomása van, tehát a párok száma legalább 3n. Másfelől, minden állomáson legfeljebb három vonal halad át, tehát legfeljebb háromszor annyi pár van, mint állomás. Ebből következik, hogy az állomások száma legalább n, vagyis a feladat állítása igaz.

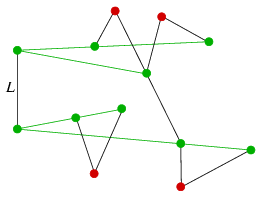
Tegyük most fel, hogy van olyan metróvonal, amelynek csak két állomása van. Legyen L egy ilyen vonal. Az L két állomásán legfeljebb 4 további metróvonal halad át; nevezzük ezeket ,,közeli'' metróvonalaknak. A további, legalább n-5 voanalat nevezzük ,,távoli'' vonalnak.

Színezzük a közeli vonalakon levő állomásokat zöldre, a többi állomást pirosra. A zöld állomások száma legyen z, a pirosaké p.

A távoli metróvonalak mindegyike legalább két állomásból áll. Egy zöld állomáson legfeljebb két, egy piros állomáson pedig legfeljebb három távoli vonal halad át, ezért 2(n-5)2z+3p.

A távoli metróvonalak mindegyikéhez van olyan metróvonal, ami L-lel összeköti. Ezért mindegyik távoli vonal tartalmaz legalább egy zöld állomást. Egy zöld állomáson legfeljebb két távoli metróvonal haladhat át, ezért n-52z.

A kapott egyenlőtlenségekből

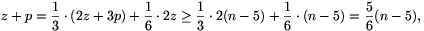
összesen tehát legalább 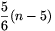állomás van.

Megjegyzés. A feladat állításában az 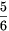konstans éles. Ha n=6k+1, akkor az alábbi ábrán a metróvonalaknak egy olyan elrendezése látható, amelyben az állomások száma 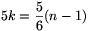.