Fizikából kitűzött gyakorlatok és feladatok
2002. május

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 234. A rostos gyümölcslevek viszkozitása hűtés hatására nő, hígítás hatására csökken. Végezzünk méréseket annak eldöntésére, hogy a két hatás közül melyik az ,,erősebb''! Mi történik a viszkozitással, ha az abszolút hőmérsékletet és a koncentrációt ugyanolyan arányban (pl. 5, 10, 15 százalékkal) csökkentjük? Keressünk olyan módszert, amellyel a viszkozitások aránya egyszerűen mérhető? (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3531. Néhány kiránduló a Tiszán csónakot bérelt 3 órára. A folyó sebessége 2,5 km/h, a csónaké a vízhez képest 7,5 km/h. Mennyire távolodhatnak el a kikötőtől, ha 3 óra alatt vissza akarnak érni? (3 pont)

Szolnok megyei általános iskolai verseny

P. 3532. Az ábrán látható nyújthatatlan fonál felső végét a mennyezethez rögzítjük, az alsó végére pedig egy m tömegű testet kötünk. A test alsó részéhez egy rugót erősítünk, amelyen 2m tömegű test lóg. A rendszer egyensúlyban van. A rugó megnyúlása 30 cm. Égessük el a fonalat!

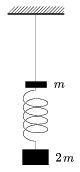
a) Mekkora az egyes testek gyorsulása közvetlenül a fonál elégetése után?

b) Mennyi idő múlva lesz a rugó először nyújtatlan állapotban, és mekkora a testek sebessége ebben a pillanatban? (5 pont)

Közli: Szűcs József, Pécs

(Párkányi László fizikaverseny)

P. 3533. Egy 10 000 m²-es sík területre időben egyenletesen, a hely szempontjából pedig egyenletes rendezetlenségben 41 másodpercig esik a jég. Az egyforma, gömböknek tekinthető jégdarabok olyan talajra hullanak, amelybe csupán kissé nyomódnak bele, ugyanakkor csak azok mozdulnak tovább beérkezési helyükről, amelyek a társaikra estek. Az utolsó másodpercben lehullott 20 000 jégdarab közül 200 esett az első 40 másodpercben lehullott valamelyik társára. a) A terület hány százalékát borítja jég? b) Mekkora egy jéggömb főkörének területe? (5 pont)

Közli: Édes Zoltán, Tata

P. 3534. 20 cm vastag, 0 ^oC hőmérsékletű, 0,25 kg/dm³ sűrűségű hótakaróból milyen vastag réteg olvad meg a napsugárzás hatására 5 órányi, a hóréteggel átlagosan 25^o-os szöget bezáró napsütés esetén? A Napból a légkör felső határán minden 1 m² nagyságú, a sugárzásra merőleges felületre érkező sugárzási teljesítmény átlagosan 1350 W. Ennek 50%-a elnyelődik a légkörben, és a hó a leérkező energia 90%-át visszaveri. (4 pont)

Közli: Holics László, Budapest

P. 3535. Az ábrán látható, egyik végén beforrasztott, A keresztmetszetű, derékszögben kétszer meghajlított cső függőleges síkban helyezkedik el. A cső függőleges részében lévő, kezdetben L=38 cm hosszúságú és T₀ hőmérsékletű levegőoszlopot 2L hosszúságú higanyoszlop zárja el. A cső vízszintes részének hosszúsága L. A külső p₀ légnyomás 2L magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. Jelöljük L^.A-t V₀-lal!

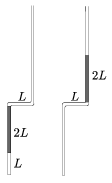
a) Adjuk meg p₀V₀ egységekben, hogy mekkora munkát végez a táguló levegő azon folyamat során, mialatt a higany éppen átfolyik a felső függőleges csőbe.

b) A levegővel közölt hő hány százaléka növelte a belső energiát?

c) Ábrázoljuk a levegő hőmérsékletét a térfogat függvényében! (5 pont)

Közli: Kotek László, Pécs

(Mikola-verseny, Sopron)

P. 3536. 5 keV energiájú, kicsit széttartó elektronnyaláb érkezik homogén mágneses mezőbe. A részecskék sebessége B irányával kicsiny szöget zár be. Mekkora legyen a mágneses indukció értéke, hogy az elektronok 10 cm távolságonként újra és újra egy pontban találkozzanak? (5 pont)

Tornyai Sándor verseny, Hódmezővásárhely

P. 3537. A Compton-szórás (rugalmas foton-elektron ütközés) során a meglökött - kezdetben nyugvónak tekintett - elektron lendülete nagyobb lett, mint a beeső f frekvenciájú fotoné volt. Legalább mekkora szögben szóródott a foton? (5 pont)

Közli: Varga István, Békéscsaba

P. 3538. Egy elektron mozgási energiája n-ed része, lendülete n-szerese valamely foton energiájának, illetve lendületének. Mekkora n értékek esetén láthatók az ilyen fotonok? (4 pont)

A Budó-verseny egyik feladata nyomán

P. 3539. Kinyújtott kezünkben tartunk egy f=12 cm fókusztávolságú gyűjtőlencsét, melyen át egy 60 méterre lévő, 24 méter magas tornyot figyelünk. Becsült adatok felhasználásával határozzuk meg a szemünk retináján létrejövő kép nagyságát! Hányszor nagyobbnak vagy kisebbnek látjuk a tornyot a lencsén keresztül, mint szabad szemmel? Hány dioptriás a szemünk az egyik, illetve a másik esetben? (5 pont)

Közli: Honyek Gyula, Budapest

P. 3540. A napkitöréseket figyelő SOHO műhold mindig a Napot és a Földet összekötő egyenesen helyezkedik el. Milyen messze van a SOHO a Földtől? (A Föld pályáját tekintsük körnek!) (6 pont)

Közli: Korpássy Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. június 11.

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 9. A reális gázok viselkedése eltér az ideálistól. Ezt az eltérést a p(V-b)=nRT állapotegyenlettel próbáljuk figyelembe venni, ahol b egy (a mérési adatokból maghatározandó) állandó. Feltételezzük, hogy a kérdéses gáz állandó térfogaton mért c_V fajhője nem függ a hőmérséklettől.

a) Mutassuk meg, hogy a fenti feltevéseknek eleget tevő gáz belső energiája csak a gáz hőmérsékletétől függ!

b) Igazoljuk, hogy 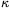=c_p/c_V független T-től is és p-től is!

c) Vezessük le az adiabatikus állapotváltozás egyenletét!

d) Milyen mikroszkopikus modell írhatná le a kérdéses gázt? Mi a b mennyiség szemléletes jelentése a modellben?

Útmutatás: Vizsgáljunk olyan körfolyamatokat, amelyek a V-T diagramon kicsiny téglalapokkal szemléltethetők! Használjuk ki, hogy az entrópia állapotjelző!