A 2002. decemberi informatika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

I. 37. Készítsünk programot (I37.pas, ...), amely egy A (2$\displaystyle \le$A $\displaystyle \le$100) alapú számrendszerben felírt fixpontos valós számot (legfeljebb 100 jegy van a tizedespontja előtt, valamint a tizedespontja mögött is) átalakít B alapú (2 $\le$ B $\le$ 100) számrendszerben felírt számmá. (10 pont)

Megoldás:

Átváltás számrendszerek között Egész számok átváltása Egész számokat, valamint tört számok egészrészét leggyakrabban a következő két módszer valamelyikével váltják át adott számrendszerből (A) egy másikba (B). B-vel osztás A alapú számrendszerben Ez az a módszer, ahogy rendszerint papíron 10-es számrendszerből egy másik számrendszerbe váltunk át. Ekkor ugyanis A=10, tehát a műveletet 10-es számrendszerben kell elvégezni, ahogy megszoktuk.
A módszer alapelve az, hogy az átváltandó számot maradékosan elosztjuk B-vel, a maradék lesz a B számrendszerbeli szám legalacsonyabb (illetve következő) helyiértéke, a hányadossal pedig újra ugyanezt tesszük, mindaddig, amíg a hányados nem nulla.

Függvény Átvált_oszt(X:TNagyEgész,B:egész):TNagyEgész
	A := X.szr
	Y.szr := B
	i := 0
	Ciklus amíg X ? 0
		Y[i] := X MODA B
		X := X DIVA B
		i := i + 1
	Ciklus vége
Eljárás vége

A-val szorzás B alapú számrendszerben Ez a módszer is használatos a gyakorlatban, viszont az előzővel ellentétben akkor, ha egy másik számrendszerből váltunk 10-esbe. Nem meglepő, hiszen itt B alapúban kell a műveletet végezni, és ekkor B=10.
A teendő az, hogy elvégezzük a számrendszer definíciójában kijelölt műveleteket, azaz egyenként megszorozzuk a számjegyeket a megfelelő helyiértékkel, és ezeket összeadjuk úgy, hogy a műveleteket a B alapú számrendszerben végezzük. A következő algoritmus ennél kicsit hatékonyabb, hiszen kikerüli az A-hatványok külön-külön történő kiszámolását:

Függvény Átvált_szoroz(X:TNagyEgész,B:egész):TNagyEgész
	A := X.szr
	Y.szr := B
	Y := 0
	Ciklus i := X.jegy-1-től 0-ig 1-esével
		Y := Y *B A +B X[i]
	Ciklus vége
Eljárás vége

Papp Szabolcs lógia kéziratából

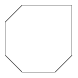
I. 38. Egy szakaszból (x1,y1,x2,y2) sokféle síkbeli alakzatot készíthetünk transzformációk sorozatával. A legegyszerűbb esetben a szakaszt eltoljuk (paramétere a dx és a dy valós számok), s eltolás közben a végpontjait folyamatosan rajzoljuk.

1. Példa: A szakasz: (100,100,100,200), a három eltolás (dx,dy): (50,0), (20,30), (40,10).

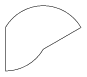
Eltolás mellett menet közben nagyítást is alkalmazhatunk (az első végpontjából nézve s-szeresre nagyíthatunk). Ekkor a művelet első két paramétere az eltolás, harmadik paramétere pedig a nagyítás.

2. Példa: A szakasz: (100,100,100,200), a három művelet (dx,dy,s): (50,-50,2), (100,0,1), (50,0,0.75).

Végül a harmadik párhuzamosan végrehajtható művelet legyen a forgatás. Paramétere a forgatás középpontja (a szakasz mentén a szakasz első végpontjától hány szakaszhossznyira helyezkedik el: t), és a forgatás f szöge fokban, az óramutató járásával ellenkező irányban.

3. Példa: A szakasz: (100,100,100,200), a két művelet (dx,dy,s,t,f): (0,0,1,0,60), (0,0,1,1,-120).

A forgatás középpontja persze kívül is lehet a szakaszon, ekkor különlegesen érdekes ábrákat kaphatunk.

4. Példa: A szakasz: (100,150,100,200), az egyetlen művelet (dx,dy,s,t,f): (0,0,1,-1,180).

5. Példa: A szakasz: (100,100,100,200), a két művelet (dx,dy,s,t,f): (50,0,1,-0.5,60), (25,25,2,1.5,-90).


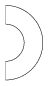1. Példa	2. Példa	3. Példa	4. Példa	5. Példa

Készítsünk programot (I38.pas, ...), amely beolvassa a szakasz végpontjait, majd az N darab művelet paramétereit, majd kirajzolja a keletkezett alakzatot. (10 pont)

Megoldás:

Algoritmus sikbeli;
  Konstans
    maxn=100;
    szor=128;
    gyok=7;
  Típus
    szakasz=(x1:Valós X y1:Valós X x2:Valós X y2:Valós);
    muvelet=(dx:Valós X dy:Valós X s:Valós X t:Valós X fok:Valós);
  Változó
    sz,uj: szakasz;
    i,j,n: Egész;
    muv:Tömb(1..maxn:muvelet);
    fx,fy,szx1,szy1,szx2,szy2: Valós;

Beolvassuk a szakasz végpontjait.

  Be: sz.x1, sz.y1, sz.x2, sz.y2;

Beolvassuk a műveletek számát. Majd beolvassuk a műveleteket is és a fokban megadott értékeket radiánba számoljuk.

  Be: N;
  ciklus i:=1-től n-ig
    Be: muv[i].dx, muv[i].dy, muv[i].s, muv[i].t, muv[i].fok;
    muv[i].fok:=muv[i].fok/180*3.14159/szor;
    muv[i].dx:=muv[i].dx/szor;
	muv[i].dy:=muv[i].dy/szor;
    ciklus j:=1-től gyok-ig
      muv[i].s:=sqrt(muv[i].s);
	ciklus vége;
  ciklus vége;
  GrafikusKépernyőInicializálása;

Kirajzoljuk a kezdeti szakaszt.

  Vonal(Kerekít(sz.x1),Kerekít(sz.y1),Kerekít(sz.x2),Kerekít(sz.y2));

Majd az N darab műveletet kiszámoljuk, illetve kirajzoltatjuk.

  ciklus i:=1-től n-ig
    ciklus j:=1-től szor-ig
      fx:=sz.x1+muv[i].t*(sz.x2-sz.x1);
      fy:=sz.y1+muv[i].t*(sz.y2-sz.y1);
      szx1:=(sz.x1-fx)*cos(muv[i].fok)+(sz.y1-fy)*sin(muv[i].fok)+fx;
      szy1:=(sz.y1-fy)*cos(muv[i].fok)-(sz.x1-fx)*sin(muv[i].fok)+fy;
      szx2:=(sz.x2-fx)*cos(muv[i].fok)+(sz.y2-fy)*sin(muv[i].fok)+fx;
      szy2:=(sz.y2-fy)*cos(muv[i].fok)-(sz.x2-fx)*sin(muv[i].fok)+fy;
      uj.x1:=szx1+muv[i].dx;
      uj.y1:=szy1+muv[i].dy;
      uj.x2:=(szx2-szx1)*muv[i].s+szx1+muv[i].dx;
      uj.y2:=(szy2-szy1)*muv[i].s+szy1+muv[i].dy;
      Vonal(Kerekít(sz.x1),Kerekít(sz.y1),Kerekít(uj.x1),Kerekít(uj.y1));
      Vonal(Kerekít(sz.x2),Kerekít(sz.y2),Kerekít(uj.x2),Kerekít(uj.y2));
      sz:=uj;
    ciklus vége;
  ciklus vége;

Kirajzoljuk az utolsó szakaszt.

  Vonal(Kerekít(uj.x1),Kerekít(uj.y1),Kerekít(uj.x2),Kerekít(uj.y2));

Visszaállítjuk a karakteres képernyőt.

  GrafikusKépernyőLezárása;
algoritmus vége.

A megoldás Pascal nyelven: Letöltés

I. 39. A nemnegatív racionális számokat egyértelműen felírhatjuk törtként, $\displaystyle A\frac{b}{c}$ alakban, ahol A $\ge$ 0, b $\ge$ 0, c>0, b<c, valamint b és c relatív prím (A, b, c egész számok). Ha A=0, akkor az alak: $\displaystyle \frac{b}{c}$, ha pedig b=0, akkor A. Készítsünk táblázatot (I39.xls), amelyben az összeadás két operandusát beírva, az összeget kapjuk meg.

Példa:

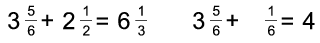
(10 pont)

Megoldás:

Három lépésben számoljuk ki a törtek összegét. Először egyszerűen az egészek összegét vesszük, illetve a törteket közös nevezőre hozzuk, oly módon, hogy összeszorozzuk őket.

G9:=A3+D3
H9:=HA(B4=0;E3;HA(E4=0;B3;B3*E4+E3*B4))
H10:=HA(B4=0;E4;HA(E4=0;B4;B4*E4))

A második lépésben a tört egész részét növeljük, míg a számlálót csökkentjük, úgy hogy a törtrész nulla és egy között legyen. Tehát a nevezővel osztunk maradékosan.

G6:=HA(H10=0;G9;G9+INT(H9/H10))
H6:=HA(H10=0;0;MARADÉK(H9;H10))
H7:=H10

A harmadik lépés előtt ki kell számolnunk a számláló és a nevező legnagyobb közös osztóját, hogy azzal le tudjunk osztani. Az LNKO-t a "J" illetve "K" jelű oszlopban számoljuk ki és az "L1" cellába írjuk. Az első sorba a számlálót és a nevezőt kell írni, majd az euklideszi algoritmus segítégével meghatározzuk a következő lépés értékeit úgy, hogy a nagyobbat elosztjuk a kisebbel.

J1:=MIN(H6;H7)
K1:=MAX(H6;H7)

J3:=HA(J2=0;0;MARADÉK(K2;J2))
K3:=J2

L1:=INDEX(K1:K11;HOL.VAN(0;J1:J11;0);1)

Végül a számlálót is és a nevezőt is leosztjuk a legnagyobb közös osztóval.

G3:=G6
H3:=HA(H6=0;"";H6/L1)
H4:=HA(H6=0;"";H7/L1)

A megoldás Excelben: Letöltés

Már regisztráltál?
Új vendég vagy?