A 2003 januári A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 308. Az A, B, C, D, E pontok úgy helyezkednek el a síkban, hogy AB=BC=CD=DA=1, és AE, BE, CE és DE mindegyike legfeljebb 1. Legfeljebb mekkora lehet AE+BE+CE+DE+AC+BD?

Megoldás. Ha A,B,C,D egy egységnyi oldalú négyzet csúcsai, E a négyzet belsejében fekszik és az egyik oldallal szabályos háromszöget alkot, akkor $\displaystyle AE+BE+CE+DE+AC+BD=2+\sqrt2+\sqrt6\approx5,8637$ (1. ábra). Megmutatjuk, hogy ez a legnagyobb lehetséges érték.

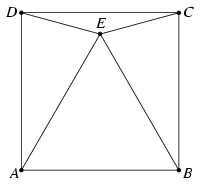
1. ábra

Többször felhasznájuk a következő lemmát, illetve annak következményét:

Lemma. Legyenek P₁,...,P_n a sík pontjai, és tetszőleges X pont esetén f(X)=P₁X+...+P_nX. Ekkor, ha w₁,...,w_k nemnegatív számok, amelyekre w₁+...+w_k=1 és X₁,...,X_k tetszőleges pontok, akkor

f(w₁X₁+...+w_kX_k)$\displaystyle \le$w₁f(X₁)+...+w_kf(X_k).

Más szóval, az f függvény konvex.

Következmény. Tetszőleges konvex sokszögön az f függvény maximuma megegyezik a csúcsokban vett értékek maximumával.

Bizonyítás. Legyen Y=w₁X₁+...+w_kX_k. Ekkor

$\displaystyle f(Y)=\sum_{i=1}^nP_iY= \sum_{i=1}^n\left|\sum_{j=1}^kw_j\vec{P_iX_j}\right|\le$

$\displaystyle \le\sum_{i=1}^n\sum_{j=1}^kw_jP_iX_j= \sum_{j=1}^kw_j\sum_{i=1}^nP_iX_j=\sum_{j=1}^kw_jf(X_j).$

Ha az X₁,...,X_n pontokban vett maximum m, akkor

$\displaystyle f(Y)\le\sum_{j=1}^kw_jf(X_j)\le\sum_{j=1}^kw_jm=m.$

Mivel az X₁,...,X_n pontok konvex burkának tetszőleges pontja előáll w₁X₁+...+w_nX_n alakban, ezzel a kövektezményt is igazoltuk.

Az A,B,C,D pontok elhelyezkedésétől függően több esetet vizsgálunk meg.

1. eset: Az A és a C pont egybeesik. Legyen T az a pont, amely a B,C,D pontokat paralelogrammává egészíti ki. (Ha A=C a BD szakasz felezőpontja, akkor T=A. ha B=D, akkor T az A pont tükörképe B-re.) Az E pontnak a B, C és D középpontú, zárt körlemezek közös részébe kell esnie. Ez a BAD szögtől függően többféle alakú lehet (2. ábra).

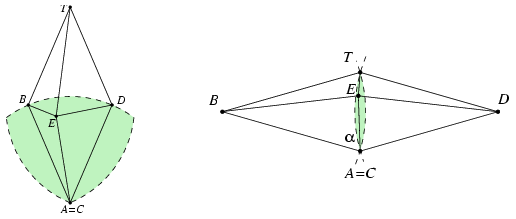
2. ábra

Mindegyik esetben igaz, hogy AE$\displaystyle \le$AT. A BAT$\displaystyle \angle$=$\displaystyle \alpha$ jelölést bevezetve,

AE+BE+CE+DE+AC+BD$\displaystyle \le$AT+1+1+1+0+BD=

$\displaystyle =3+2\sin\alpha+2\cos\alpha=3+2\sqrt2\sin(\alpha+45^\circ)\le3+2\sqrt2<5,83.$

Ebben az esetben tehát nem lehet elérni a fenti példánál nagyobb összeget.

Hasonlóan intézhetjük el azt az esetet, amikor B és D egybeesik.

2. eset: Az A, B, C, D pontok egy rombusz csúcsai, és a rombusz egyik szöge legalább 120 fokos. A szimmetria miatt feltehetjük, hogy a rombusz A-nál és C-nél levő szöge legalább 120^o, továbbá az E pont az AC egyenesnek a B-t tartalmazó oldalán helyezkedik el.

Az a halmaz, ahol az E pont elhelyezkedhet, a B és D sugarú, egységnyi sugarú körlemezek metszete; ezt két körív határolja (3. ábra).

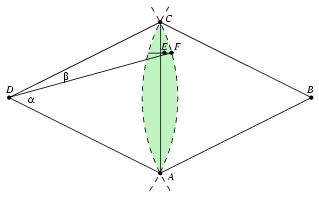
3. ábra

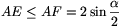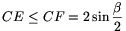Állítsunk merőlegest az E pontból az AC egyenesre; messe ez a D középpontú körívet F-ben. Legyen továbbá ADF$\displaystyle \angle$=$\displaystyle \alpha$, CDF$\displaystyle \angle$=$\displaystyle \beta$. Ekkor $\displaystyle \alpha$+$\displaystyle \beta$ $\le$ 60^o, $AE\le AF=2\sin{\alpha\over2}$ , $CE\le CF=2\sin{\beta\over2}$ és

AE+BE+CE+DE+AC+BD $\le$

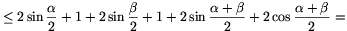
$\le2\sin{\alpha\over2}+1+2\sin{\beta\over2}+1+ 2\sin{\alpha+\beta\over2}+2\cos{\alpha+\beta\over2}=$

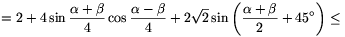
$=2+4\sin{\alpha+\beta\over4}\cos{\alpha-\beta\over4}+ 2\sqrt2\sin\left({\alpha+\beta\over2}+45^\circ\right)\le$

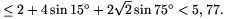
$\le2+4\sin15^\circ+2\sqrt2\sin75^\circ<5,77.$

3. eset: Az A, B, C, D pontok egy rombusz csúcsai, és a rombusznak mindegyik szöge kisebb 120 foknál. Ebben az esetben a lehetséges E pontok halmazát négy körív határolja. Első lépésként az E pontot ennek a tartománynak a határára mozgatjuk úgy, hogy közben az AE+BE+CE+DE összeg nem csökken. Húzzunk E-n keresztül egy tetszőleges egyenest. Ez a tartomány hatását messe az F és G pontokban. A lemma alapján az AF+BF+CF+DF és AG+BG+CG+DG összegek valamelyike legalább akkora, mint AE+BE+CE+DE (4. ábra).

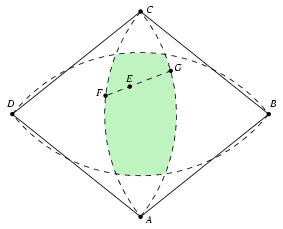
4. ábra

Az E pontot ide mozgatva, a vizsgált összeg nem csökken. Elég tehát a zöld tartomány határán levő pontokat vizsgálni; a szimmetria miatt feltehetjük, hogy AE=1. Az ilyen pontok egy A sugarú köríven helyezkednek el; ennek végpontjait jelöljük U-val és V-vel (5. ábra).

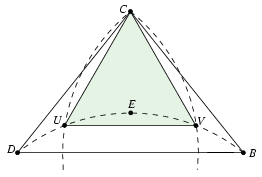
5. ábra

Vizsgáljuk most az f(X)=BX+CX+DX függvényt a CUV háromszögben. A lemma szerint a függvény maximuma az egyik csúcsban van. Mivel BU=1 és a háromszög-egyenlőtlenség szerint DU+CU>CD=1, f(U)=f(V)=BU+CU+DU>2. Ugyanakkor f(C)=2, tehát a függvény maximuma az U és a V pontokbeli érték. Mivel az E pont az UV körívvel együtt a CUV háromszögben van, BE+CE+DE $\le$ BU+CU+DU. Ezen kívül AE=AU=1, ezért AE+BE+CE+DE $\le$ AU+BU+CU+DU.

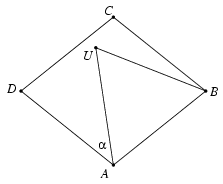
6. ábra

Legyen DAU $\angle$ = $\alpha$ (6. ábra). Az ABU háromszög szabályos, és a szögek összeszámolásából

AU+BU+CU+DU+AC+BD=

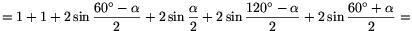
$= 1+1+2\sin{60^\circ-\alpha\over2}+2\sin{\alpha\over2} +2\sin{120^\circ-\alpha\over2} +2\sin{60^\circ+\alpha\over2} =$

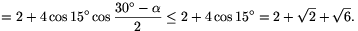
$= 2+4\cos15^\circ\cos{30^\circ-\alpha\over2}\le2+4\cos15^\circ=2+\sqrt2+\sqrt6.$

Megjegyzés. Több versenyző csak azzal az esettel foglalkozott, amikor az A, B, C, D pontok egy rombusz csúcsai. Ők 3 pontot kaptak.

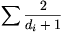A. 309. Egy n csúcsú egyszerű gráfban a csúcsok fokszámai rendre 0<d₁ $\le$ ... $\le$ d_n. Bizonyítsuk be, hogy kiválasztható legalább $\sum\frac{2}{d_i+1}$ csúcs úgy, hogy az általuk kifeszített részgráfban nincs kör.

1. megoldás. Az állítást teljes indukcióval igazoljuk. Az n=0 esetben az üres gráf teljesíti a feltételeket, és a kiválasztandó pontok száma is éppen 0. Az n=1 eset nem lehetséges, mert a gráfban nem lehet izolált pont. Az n=2 esetben csak a teljes gráf, azaz d₁=d₂=2 lehetséges, a kiválasztandó pontok száma 2.

A továbbiakban legyen n $\ge$ 3, és tegyük fel, hogy kevesebb pontból álló gráfokra az állítás igaz. A következő három esetet fogunk vizsgálni, amelyek közül legalább az egyik mindig teljesül:

1. eset: van olyan elsőfokú csúcs, amelynek a szomszédja is elsőfokú.

2. eset: van olyan elsőfokú csúcs, amelynek a szomszédja legalább másodfokú.

3. eset: nincs elsőfokú csúcs, azaz minden csúcs legalább másodfokú.

Az 1. esetben legyen ez a két csúcs A és B. Ezt a két pontot válasszuk ki és alkalmazzuk az indukciós feltevést a gráf többi pontjára. A többi pont fokszáma d₃,...,d_n, ezért legalább 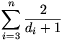$\sum_{i=3}^n{2\over d_i+1}$ pontot tudunk kiválasztani közülük úgy, hogy ne alkossanak kört. Az A és B pontokkal együtt ez legalább 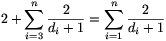$2+\sum_{i=3}^n{2\over d_i+1}=\sum_{i=1}^n{2\over d_i+1}$ . Az 1. esetben tehát az állítás igaz.

A 2. esetben legyen az elsőfokú pont A, szomszédja a j-edik pont; a feltétel szerint d_j $\ge$ 2. A gráfból válasszuk ki A-t; mivel A elsőfokú, nem megy át rajta egy kör sem. Tekintsük azt a G' részgráfort, amit a többi pont feszít ki. Ebben a gráfban a csúcsok fokszámai d₂,...,d_j-1,d_j-1,d_j+1,dots,d_n. A G' gráfban tehát az indukciós fetevés szerint kiválasztható legalább

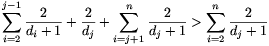
$\sum_{i=2}^{j-1}{2\over d_i+1}+{2\over d_j}+\sum_{i=j+1}^n{2\over d_j+1}>\sum_{i=2}^n{2\over d_j+1}$

pont, amelyek által kifeszített részgráfban nincs kör. Ezek az A ponttal együtt megfelelő halmazt adnak.

A 3. esetben legyen A az n-edik pont, amely az (egyik) legnagyobb fokszámú; szomszédai legyenek az 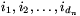$i_1,i_2,\dots,i_{d_n}$ -edik pontok. Hagyjuk el a gráfból A-t és a belőle induló éleket, és válasszunk ki pontokat a megmaradó gráfból. Az indukciós feltevés szerint a kiválasztható pontok száma legalább

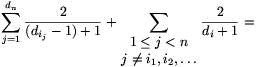
$\sum_{j=1}^{d_n}{2\over(d_{i_j}-1)+1}+\sum_{\matrix{1\le j<n\cr j\ne i_1,i_2,\dots\cr}}{2\over d_i+1}=$

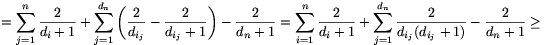
$=\sum_{j=1}^n{2\over d_i+1}+\sum_{j=1}^{d_n}\left({2\over d_{i_j}}-{2\over d_{i_j}+1}\right)-{2\over d_n+1}= \sum_{i=1}^n{2\over d_i+1}+\sum_{j=1}^{d_n}{2\over d_{i_j}(d_{i_j}+1)}-{2\over d_n+1}\ge$

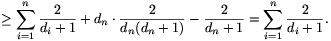
$\ge\sum_{i=1}^n{2\over d_i+1}+d_n\cdot{2\over d_n(d_n+1)} -{2\over d_n+1}=\sum_{i=1}^n{2\over d_i+1}.$

2. megoldás. Vegyük a csúcsok egy tetszőleges sorba rendezését, és jelöljük meg azokat a csúcsokat, amiket legfeljebb egy szomszédjuk előz meg a permutációban.

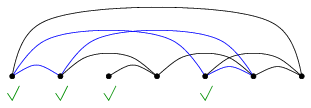
A gráf tetszőleges körében az a pont, ami a rendezésben leghátul áll, biztosan nincs megjelölve, mert mindkét, a körben szereplő szomszédja megelőzi. (Lásd az ábrán a kék színnel jelölt kört.) A megjelölt pontok tehát egy olyan részgráfot feszítenek ki, amiben nincs kör.

Ha a sorbarendezést véletlenszerűen választjuk, akkor egy d fokú csúcsot 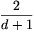${2\over d+1}$ valószínűséggel jelölünk meg. Az összes megjelölések számának várható értéke tehát 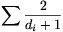$\displaystyle\sum{2\over d_i+1}$ . Ezért van olyan permutáció, amiben legalább ennyi a megjelölt csúcsok száma.

A. 310. Legyen tetszőleges n pozitív egészre

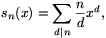
$s_n(x)=\sum_{d\mid n}\frac{n}{d}x^d,$

és definiáljuk a p₀,p₁,... polinomokat a következő rekurzióval: p₀(x)=1,

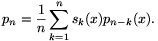
$p_n=\frac{1}{n}\sum_{k=1}^ns_k(x)p_{n-k}(x).$

Igazoljuk, hogy a p_n polinom mindegyik együtthatója egész szám.

1. megoldás (Csóka Endre megoldása). Jelöljük tetszőleges m,n nemnegatív számok esetén a_n,m-mel az n szám m-tagú partícióinak számát, vagyis azt, hogy az n hányféleképpen írható fel m darab pozitív egész összegeként, ha a sorrend nem számít, és a tagok között lehetnek egyenlők is. Például a_9,3=5, mert a 9 összesen ötféleképpen írható fel háromtagú összegként: 9=1+2+6=1+3+5=1+4+4=2+3+4=3+3+3. Definiáljuk a_0,0=1-et is, az üres (0-tagú) összeg értékét 0-nak tekintve.

Teljes indukcióval bebizonyítjuk, hogy tetszőleges n pozitív egészre p_n(x)=a_n,0+a_n,1x+a_n,2x²+...+a_n,nxⁿ. Az állítást kis n-ekre könnyen ellenőrizhetjük:

p₀(x)=1,

p₁(x)=s₁(x)p₀(x)=x^.1=x,

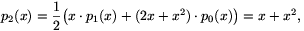
$p_2(x)={1\over2}\big(x\cdot p_1(x)+(2x+x^2)\cdot p_0(x)\big)=x+x^2,$

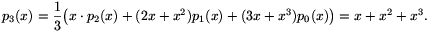
$p_3(x)={1\over3}\big(x\cdot p_2(x)+(2x+x^2)p_1(x)+(3x+x^3)p_0(x)\big) =x+x^2+x^3.$

Az (1) rekurzió alapján

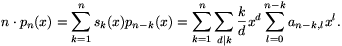
$n\cdot p_n(x)=\sum_{k=1}^ns_k(x)p_{n-k}(x)=\sum_{k=1}^n\sum_{d|k}{k\over d}x^d\sum_{l=0}^{n-k}a_{n-k,l}x^l.$

Az m-edfokú tagokat összehasonlítva, azt kell igazolnunk, hogy

(2)	$n\cdot a_{n,m}=\sum_{k=1}^n\sum_{d\|k}{k\over d}\cdot a_{n-k,m-d}=\sum_{d=1}^n\sum_{h=1}^{[n/d]}h\cdot a_{n-hd,m-d}.$

Ábrázoljuk az n szám m-elemű partícióit egymás mellé helyezett rácstéglalapokkal úgy, hogy a téglalapok szélessége megfeleljen az egyes tagoknak és a szélességek mindig növekvő sorrendben legyenek. A téglalapokban szereplő rácsnégyzetek közül az egyiket jelöljük meg. Az ilyen módon, egy ponton megjelölt ábrázolások száma n^.a_n.

Most minden megjelölt ábrázolással végezzük el a következő műveletet. Vizsgáljuk meg, hogy a megjelölt mező mekkora téglalapban szerepel; legyen a téglalap szélessége h. Hagyjuk el a partícióból ezt a téglalapot és mindazokat a h szélességű téglalapokat, amelyek a megjelölt mezőtől balra helyezkednek el. (Az ábra az n=5, m=3 esetre mutatja be a megfeleltetést.)

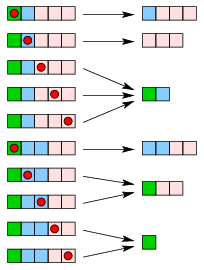
Ha az elhagyott téglalapok száma d, akkor a megmaradt téglalapok az n-hd szám egy (m-d)-elemű partícióját ábrázolják. Vizsgáljuk meg, hogy hányszor kapjuk ezt az partíciót. Az n-hd és m-d számok meghatározzák d-t és h-t. A megjelölt négyzetnek a h szélességű téglalapok közül a d-edikben kell lennie. A megjelölt négyzet tehát összesen h-féle lehet. Ezért az n-hd szám minden egyes (m-d)-tagú partícióját pontosan h-szor kapjuk meg. Ezzel igazoltuk, hogy 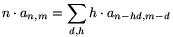$n\cdot a_{n,m}=\sum_{d,h}h\cdot a_{n-hd,m-d}$ .

2. megoldás. Rögzített x értékre vizsgáljuk a

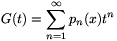
$G(t)=\sum_{n=1}^\infty p_n(x)t^n$

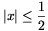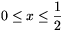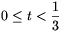generátorfüggvényt. A polinomok definíciójából leolvasható, illetve indukcióval könnyen igazolható, hogy $|x|\le{1\over2}$ esetén |s_n(x)|<2n és |p_n(x)| $\le$ 3ⁿ, ezért a generátorfüggvény definíciója $0\le x\le{1\over2}$ , $0\le t<{1\over3}$ esetén biztosan értelmes. A polinomok definícióját behelyettesítve G deriváltjába,

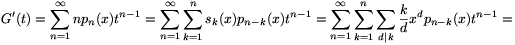
$G'(t)=\sum_{n=1}^\infty np_n(x)t^{n-1} =\sum_{n=1}^\infty\sum_{k=1}^ns_k(x)p_{n-k}(x)t^{n-1} =\sum_{n=1}^\infty\sum_{k=1}^n\sum_{d|k}{k\over d}x^dp_{n-k}(x)t^{n-1}=$

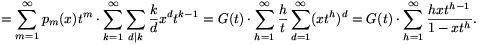
$=\sum_{m=1}^\infty p_m(x)t^m\cdot\sum_{k=1}^\infty\sum_{d|k}{k\over d}x^dt^{k-1}=G(t)\cdot\sum_{h=1}^\infty{h\over t}\sum_{d=1}^\infty(xt^h)^d=G(t)\cdot\sum_{h=1}^\infty{hxt^{h-1}\over1-xt^h}.$

(m=n-k és h=k/d. Mivel minden tag pozitív, az összegzések tetszés szerint felcserélhetők.) G(t)-vel osztva:

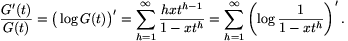
${G'(t)\over G(t)}=\big(\log G(t)\big)'= \sum_{h=1}^\infty{hxt^{h-1}\over1-xt^h}= \sum_{h=1}^\infty\left(\log{1\over1-xt^h}\right)'.$

Integrálva és figyelembe véve, hogy hogy G(0)=1,

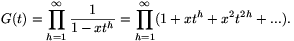
$G(t)=\prod_{h=1}^\infty{1\over1-xt^h}= \prod_{h=1}^\infty(1+xt^h+x^2t^{2h}+...).$

Ebből az alakból leolvasható, hogy p_n(x), ami tⁿ együtthatója, minden n-re egy-egy egész együtthatós polinomja x-nek. Az is leolvasható, hogy x^mtⁿ együtthatója nem más, mint az n szám m-tagú partícióinak száma.

Már regisztráltál?
Új vendég vagy?