A 2003. márciusi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3622.

(4 pont)

Megoldás: Ha a törpikék találnak egy 21x35 méteres téglalap alakú részt az erdőben, amelynek belsejébe egyetlen fenyőfa törzsének középpontja sem esik bele, akkor annak mindegyik szélét fél méterrel beljebb tolva, az így nyert 20x34 méteres téglalap alakú rész alkalmas lesz teniszpályának. Ha a törpök találnak 7 ilyen 21x35 méteres, páronként közös pont nélküli téglalapot, akkor tervüket biztosan meg tudják valósítani.

Mivel (1001x945):(21x35)=1287, az erdő területe pontosan 1287-szerese a téglalap területének. Ha tehát egy 1001x945-ös téglalapot ki lehet parkettázni 21x35-ös téglalapokkal, akkor az erdőt ennek megfelelően parcellázva, lesz legalább 7 parcella, amelynek belsejébe egyetlen fenyőfa törzsének középpontja sem esik bele, ezekben pedig a teniszpályák kijelölhetők.

Az oldalhosszakat 7-tel osztva, elegendő lenne egy 143x135-ös téglalapot felosztani 3x5-ös téglalapokra. Itt 135 3-mal és 5-tel is osztható, 143 pedig felírható 28x5+ 3 alakban. A nagy téglalapot fel lehet tehát bontani két kisebb téglalapra, nevezetesen egy 140x135-ös és egy 3x135-ös méretűre úgy, hogy mindkét téglalapnak egyik oldala osztható 3-mal, a másik pedig 5-tel, tehát külön-külön is feloszthatók már 3x5-ös téglalapokra. A keresett felosztás tehát megvalósítható, a feladatban megfogalmazott kérdésre igenlő a válasz.

B.3623.

(4 pont)

Megoldás: Az \(\displaystyle A=\root3\of{\sqrt5+2}\), \(\displaystyle B=\root3\of{\sqrt5-2}\), x=A-B jelöléssel élve

\(\displaystyle x^3=A^3-B^3+3AB(B-A)=({\sqrt5+2})-({\sqrt5-2})-3ABx.\)

Mivel \(\displaystyle A^3B^3=({\sqrt5+2})({\sqrt5-2})=5-4=1\), kapjuk hogy AB=1 és így x³+3x-4=0. Ezt az egyenletet x=1 nyilván kielégíti, vagyis x-1 gyöktényezője az x³+3x-4 polinomnak. Ezt kiemelve

x³+3x-4=(x-1)(x²+x+4),

ahol a második tényezőnek nincsen valós gyöke. Mivel x valós szám, szükségképpen x=1, ami nyilván racionális szám.

B.3624.

\(\displaystyle \frac{{(a+b)}^n-{(a-b)}^n}{{(a+b)}^n+{(a-b)}^n}=\frac{a}{b}, \)

ahol n adott pozitív egész. Bizonyítsuk be, hogy a=b.

(4 pont)

Megoldás: A nevezőkkel beszorozva és rendezve

(a+b)ⁿ(b-a)=(a-b)ⁿ(a+b)

adódik. Ha a\(\displaystyle \ne\)b, akkor a 0-tól különböző (a+b)(b-a) számmal való leosztás után az

(a+b)^n-1=-(a-b)^n-1

összefüggést kapjuk. Ha n páratlan, akkor a baloldalon pozitív, míg a jobboldalon negatív szám áll. Ha n páros, akkor mindkét oldalnak az n-1-edik gyökét véve kapjuk, hogy a+b=-a+b, vagyis a=0, ami ellentmond annak a kikötésnek, hogy a pozitív. Tehát valóban a=b, mely esetben az eredeti egyenlőség tényleg teljesül.

B.3625.

(3 pont)

Megoldás: Legyen a tetraéder négy csúcsa A,B,C,D, ahol A a szóban forgó három lap közös csúcsa. A feladatban szereplő g' gömb a tetraéderbe írt g gömbből A középpontú nagyítással keletkezik, melynek arányát jelölje \(\displaystyle \lambda\). Legyen továbbá F a BC él felezőpontja, S az ABC lap középpontja, K pedig a tetraéder középpontja. Mivel g az ABC lapot S-ben érinti, g' pedig az ABC lapot és egyben a BC élet is az F pontban érinti, \(\displaystyle \lambda\)=AF/AS=3/2. Ezért a g' gömb sugara, r'=(3/2)r, ahol r a g gömb sugara.

Mivel O egyben a tetraéder súlypontja is, r=OS=DS/4, ahol a DS szakaszt DF és SF ismeretében a Pithagorasz tételből tudjuk meghatározni. Itt \(\displaystyle DF=AF=\sqrt{3}/2\) és SF=AF/3, vagyis

\(\displaystyle DS^2=DF^2-SF^2=\Bigl(1-{1\over9}\Bigr)DF^2={2\over3}.\)

A g' gömb sugara ezek szerint

\(\displaystyle r'={3\over2}\cdot{DS\over4}={\sqrt{3}\over4\sqrt{2}}.\)

B.3626.

(3 pont)

Megoldás: Ha x_n és x_n+1 pozitív, akkor x_n+2 értelmes és pozitív. A teljes indukció elve miatt tehát a sorozat valamennyi eleme értelmezhető, és pozitív szám lesz.

Ha x₀=a és x₁=b, akkor a rekurzió alapján

\(\displaystyle x_2={b+1\over a},\ x_3={a+b+1\over ab},\ x_4={a+1\over b},\ x_5=a,\ x_6=b.\)

Vagyis x₅=x₀, x₆=x₁, és ha valamely n természetes számra x_n+5=x_n és x_n+6=x_n+1, akkor

\(\displaystyle x_{n+7}={x_{n+6}+1\over x_{n+5}}= {x_{n+1}+1\over x_n}=x_{n+2}.\)

A sorozat tehát periodikus 5 hosszúságú periódussal, vagyis a sorozat 2003-adik tagja,

\(\displaystyle x_{2002}=x_2={b+1\over a}={x_1+1\over x_0}.\)

B.3627.

\(\displaystyle a^3+b^3+c^3+d^3\ge\max\left\{a+b+c+d;\frac{1}{a}+ \frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right\}. \)

(4 pont)

Javasolta: Némethy Katalin, Budapest

Megoldás: A számtani és mértani közepek közötti egyenlőtlenségből

\(\displaystyle {a+b+c+d\over4}\ge\root4\of{abcd}=1,\)

ahol egyenlőség csak az a=b=c=d esetben áll fenn, amikor is abcd=1 miatt mind a négy szám 1-gyel egyenlő. A számtani közép és a harmadik hatványközép közötti egyenlőtlenséget is figyelembe véve innen

\(\displaystyle {a+b+c+d\over4}\le\Bigl({a+b+c+d\over4}\Bigr)^3\le {a^3+b^3+c^3+d^3\over4}.\)

Ennek alapján

a³+b³+c³+d³\(\displaystyle \ge\)a+b+c+d,

ahol egyenlőség pontosan az a=b=c=d=1 esetben áll fenn.

Ugyancsak a fent említett közepek között fennálló egyenlőtlenségek miatt

\(\displaystyle a^3+b^3+c^3+d^3={a^3+b^3+c^3\over3}+{a^3+b^3+d^3\over3}+ {a^3+c^3+d^3\over3}+{b^3+c^3+d^3\over3}\ge\)

\(\displaystyle \ge\Bigl({a+b+c\over3}\Bigr)^3+\Bigl({a+b+d\over3}\Bigr)^3+ \Bigl({a+c+d\over3}\Bigr)^3+\Bigl({b+c+d\over3}\Bigr)^3\ge\)

\(\displaystyle \ge abc+abd+acd+bcd={1\over d}+{1\over c}+{1\over b}+{1\over a}.\)

Itt az egyenlőség szükséges és elégséges feltétele ismétcsak a=b=c=d. A kapott két eredményt összevetve nyerjük a bizonyítandó egyenlőtlenséget, melyben egyenlőség pontosan az a=b=c=d=1 esetben áll fenn.

B.3628.

(4 pont)

Megoldás: Vegyük az egyszerűség kedvéért egységnek a 180 m²-t. Ekkor a három ismert rész 2, 4, 5 egység területű.

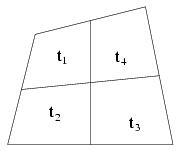
1. ábra

A négy kis négyszög területét jelölje az 1. ábra szerint t₁, t₂, t₃, t₄, a t_i területű négyszögből két oldalfelezőpont összekötésével levágott (a 2. ábrán piros) háromszög területét h_i, a teljes négyszög területét pedig T.

2. ábra

Ismeretes, hogy h₁+h₃=h₂+h₄=T/4, hiszen a négyszög egy-egy átlójával párhuzamos középvonalak vágják le a h_i területű háromszögeket, illetve t_i-h_i=T/8, mert az oldalfelezőpontok olyan paralelogrammát határoznak meg, amelynek területe a négyszög területének a fele és amelynek egy-egy negyede esik az egyes kis négyszögekbe.

Innen egyfelől t₁+t₃=t₂+t₄=T/2 következik, másrészt h_i>0 miatt t_i>T/8.

Válasszuk úgy a betűzést, hogy az ismert három terület t₁, t₂ és t₃ legyen. Ekkor t₄=t₁+t₃-t₂ és T=2(t₁+t₃). t₂ értéke szerint három lehetőségünk van:

a) t₂=2. Ekkor t₄=4+5-2=7 és T=18.

b) t₂=4. Ekkor t₄=2+5-4=3 és T=14.

c) t₂=5. Ekkor t₄=2+4-5=1 és T=12.

Az első és a harmadik eset nem jöhet létre, ugyanis az a) esetben T/8=9/4>t₂, a c) esetben pedig T/8=3/2>t₄, ellentétben a kapott t_i>T/8 feltétellel.

A második eset viszont megvalósul. Ekkor ugyanis T/8=7/4<t_i, és így h₁=1/4, h₂=9/4, h₃=13/4, h₄=5/4, a négyszög átlói tehát 1:13, illetve 9:5 arányban osztják egymást. Minden ilyen négyszög a hasonlóság erejéig meg is felel. A területe (h₁+h₃)^.4=14 egység és így a t_i=h_i+T/8 összefüggés miatt valóban rendre 2, 4, 5, 3 egységnyi részekre osztják a középvonalai.

A negyedik testvér tehát 3 egységnyi, azaz 540 m²-es telket kapott.

B.3629.

(AB+CD)²+ (BC+DA)²\(\displaystyle \ge\)(AC+BD)².

(4 pont)

Megoldás: Toljuk el a CDA háromszöget a DB vektorral, így kapjuk a C'BA' háromszöget.

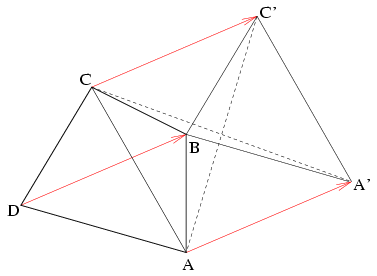
Most a CC'A'A négyszög egy paralelogramma, melynek oldalai CC'=AA'=BD és A'C'=AC. Ebben a parallelogrammában a koszinusz tételből könnyen levezethető parallelogramma szabály értelmében az átlók négyzetösszege egyenlő az oldalak négyzetösszegével, amiből

C'A²+A'C²=2(AC²+BD²)\(\displaystyle \ge\)(AC+BD)²

adódik. Itt egyenlőség pontosan akkor áll fenn, ha AC=BD.

A háromszög egyenlőtlenséget az ABC' és CBA' háromszögekre felírva kapjuk, hogy AC'\(\displaystyle \le\)AB+BC'=AB+CD és CA'\(\displaystyle \le\)BC+BA'=BC+DA, ahonnan

C'A²+A'C²\(\displaystyle \le\)(AB+CD)²+(BC+DA)²

következik. Itt egyenlőség pontosan akkor áll fenn, ha a B pont a CA' és AC' szakaszoknak is pontja, ami azzal ekvivalens, hogy az ABCD négyszög parallelogramma.

A két egyenlőtlenséget összeolvasva nyerjük a bizonyítandó állítást, ahol egyenlőség tehát pontosan akkor áll fenn, ha az ABCD négyszög egy olyan parallelogramma, melynek átlói egyenlő hosszúak, vagyis ha a szóban forgó négyszög téglalap.

B.3630.

(5 pont)

Megoldás: A három pont valamilyen sorrendben a szerkesztendő négyszög három egymást követő csúcsa lesz. Megmutatjuk, hogy mindhárom lehetséges sorrendhez lesz pontosan egy megfelelő négyszög. A három pont tehát legyen rendre az ABCD négyszög A,B és C csúcsa. A szerkesztendő ismeretlen D csúcsra legyen AD=x és CD=y. Az AB=s, BC=t jelöléseket bevezetve, az általánosság megszorítása nélkül feltehetjük, hogy s\(\displaystyle \ge\)t.

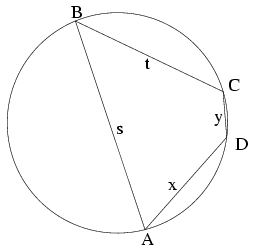
A körvonal B-t nem tartalmazó AC ívén lévő D pont pontosan akkor lesz megfelelő, ha s+y=t+x, azaz x-y=s-t, vagyis ha a D pont egy alkalmas hiperbolaágon helyezkedik el, mely hiperbolaág (s=t esetén egyenes) metszi az AC szakaszt és szimmetrikus az AC egyenesre. A teljes hiperbolát úgy kapnánk meg, ha ezt az ívet az AC szakasz felezőpontjára tükröznénk. Mivel mindkét hiperbolaág metszi az adott körvonal mindkét AC ívét, továbbá mivel egy hiperbolának egy körrel legfeljebb 4 közös pontja lehet, a keresett D pont egyértelműen meghatározott, ami az elfajuló s=t esetben is nyilvánvalóan igaz.

A keresett D pont megszerkesztésére rátérve, nekünk elegendő az x és y távolságokat megszerkesztenünk. Mivel x-y ismert, elég, ha x+y-t megszerkesztjük, innen már triviális módon szerkeszthető a D pont. Legyen ABC\(\displaystyle \angle\)=\(\displaystyle \beta\), ekkor ADC\(\displaystyle \angle\)=\(\displaystyle \delta\)=180^o-\(\displaystyle \beta\). Az ABC és ADC háromszögekre a koszinusz tételt felírva

s²+t²-2stcos \(\displaystyle \beta\)=AC²=x²+y²-2xycos \(\displaystyle \delta\).

Mivel cos \(\displaystyle \delta\)=-cos \(\displaystyle \beta\), a kapott egyenlőséget az

x²+y²-2xy=(x-y)²=(s-t)²=s²+t²-2st

összefüggéssel összevetve adódik, hogy

xy(1+cos \(\displaystyle \beta\))=st(1-cos \(\displaystyle \beta\)).

Innen \(\displaystyle x+y=\sqrt{(x-y)^2+4xy}=\sqrt{a^2+b^2}\), ahol a=s-t ismert, b pedig mint a 2s(1-cos \(\displaystyle \beta\)) és 2t/(1+cos \(\displaystyle \beta\)) szakaszok mértani középarányosa, a jól ismert módszerekkel könnyen megszerkeszthető, x+y-t pedig az a,b befogókkal rendelkező derékszögű háromszög átfogójaként kapjuk meg.

Összefoglalva, a feladatnak minden esetben pontosan három megoldása lesz, melyek a három adott pont sorrendjének lerögzítése után a fenti eljárással megszerkeszthetők.

B.3631.

(Lásd a B. 3621. feladatot.)

(5 pont)

Megoldás: Ha p és q is felcserélhető f-fel, akkor poq is felcserélhető f-fel, ugyanis

((poq)of)(x)=p(q(f(x)))=p(f(q(x)))=f(p(q(x)))=(fo(poq))(x)

teljesül minden x-re, amiből következik, hogy a (poq)of polinom azonos az fo(poq) polinommal. Ugyanez igaz természtesen a qop polinomra is. Vegyük észre, hogy ha a p(x) polinom foka n, a q(x)-é pedig m, akkor mind a poq, mind a qop polinom foka nm. Elegendő tehát belátni a következő állítást: tetszőleges k pozitív egészhez legfeljebb egy olyan r(x) k-ad fokú polinom van, amely f-fel felcserélhető.

Állításunk igazolásához keressük az r polinomot

r(x)=r_kx^k+r_k-1x^k-1+...+r₁x+r₀

alakban, ahol r_k\(\displaystyle \ne\)0. Legyen f(x)=ax²+bx+c, ahol a\(\displaystyle \ne\)0. Az r polinom pontosan akkor felcserélhető f-fel, ha

a(r_kx^k+r_k-1x^k-1+...+r₀)²+b(r_kx^k+r_k-1x^k-1+...+r₀)+c=

=r_k(ax²+bx+c)^k+r_k-1(ax²+bx+c)^k-1+...+r₀.

Mindkét oldalon egy 2k-ad fokú polinom áll. A két polinomban x^2k együtthatóját összehasonlítva az ar_k²=r_ka^k összefüggésre jutunk, ahonnan r_k=a^k-1. Ha valamilyen 0\(\displaystyle \le\)i<k esetén az r_k, r_k-1, ..., r_k-i együtthatókat már meghatároztuk, akkor r_k-i-1 is egyértelműen meghatározható, ha a két polinomban összehasonlítjuk x^2k-i-1 együtthatóját. Valóban, a második polinomban ez az együttható, t_2k-i-1 kifejezhető az a,b,c számok és a már meghatározott r_k-j (j\(\displaystyle \le\)(i+1)/2) együtthatók segítségével, azok valamilyen többváltozós polinomjaként, míg az első polinomban a megfelelő s_2k-i-1 együttható az a,b,c és r_k-j (j\(\displaystyle \le\)i+1) együtthatók polinomjaként írható fel. Látszik, hogy s_2k-i-1-ben is csak már eddig meghatározott együtthatók szerepelnek, az r_k-i-1 együttható kivételével. Mivel az s_2k-i-1 többváltozós polinom r_k-i-1-t tartalmazó tagja éppen 2ar_kr_k-i-1, az

\(\displaystyle r_{k-i-1}={t_{2k-i-1}-(s_{2k-i-1}-2ar_kr_{2k-i-1})\over2ar_k}\)

összefüggés alapján r_k-i-1 valóban meghatározható. Ilyen módon az r(x) polinom valamennyi együtthatóját meghatározhatjuk, melyeknek még k további összefüggést is ki kell elégíteniük. Ezért az r(x) polinom vagy egyértelműen meghatározható, vagy pedig nem létezik, és éppen ezt akartuk igazolni.