 |
A 2003. márciusi számban kitűzött fizika elméleti feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
P. 3601. Egy különleges gyöngysor elemei mind ugyanabból az anyagból készültek; valamennyi gömb alakú, közepén hengeres furattal. A különlegesség az, hogy bár a gömbök sugarai különbözőek, a furat hossza (a henger alkotója) mindegyik esetben pontosan ugyanakkora.
Mit állíthatunk a gyöngyök tömegéről?
(3 pont)
Közli: Vermes Miklós (1905-1990) feladata nyomán
Megoldás. Mindegyik gyöngynek ugyanakkora a tömege.
P. 3602. Fölfelé szélesedő, csonkakúp alakú pohárba ugyanakkora tömegű vizet vagy olajat öntve lesz nagyobb a pohár aljára nehezedő nyomás?
(3 pont)
Közli: Varga István, Békéscsaba
Megoldás. A víz nyomása lesz nagyobb.
P. 3603. Vízszintes talajon gördülő, egyenletesen gyorsuló, R sugarú vékonyfalú gömb belsejében kicsiny test csúszkál.
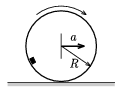
Mekkora súrlódási együttható esetén marad a test mindig R/2 távolságra a talajtól?
(4 pont)
Közli: Hortobágyi János, Bonyhád
Megoldás. \(\displaystyle \mu={\displaystyle{{\sqrt{3}g-a}\over{\sqrt{3}a+g}}}\), ha \(\displaystyle a\le\sqrt{3}g\).
Amennyiben \(\displaystyle \)\sqrt{3}g">, a test nem maradhat a talajtól R/2 távolságban.
P. 3604. A Fonyód és Badacsony között közlekedő, 20 km/h sebességgel haladó Helka motoros 100 Hz-es hangot bocsát ki, ami a pontosan szembejövő Badacsony katamaránról visszaverődik. A Helka matróza másodpercenként 7 lebegést hall. Mekkora a katamarán sebessége?
(5 pont)
Közli: Pálfalvi László, Pécs
Megoldás. 21,4 km/h.
P. 3605. Bizonyos tömegű, kétatomos ideális gáz az ábrán látható módon kétféleképpen jut el az A állapotból a B állapotba. A két folyamat során felvett hők aránya Q2:Q1=54:49.
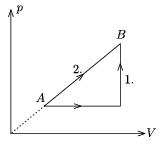
a) Határozzuk meg a két folyamat során végzett munkák arányát!
b) Mekkora a gáz hőmérséklete a B állapotban, ha az A állapotban 100 K volt?
(4 pont)
Közli: Kotek László, Pécs
Megoldás. a) \(\displaystyle {\displaystyle{W_2\over W_1}}={\displaystyle{9\over4}}.\) b) TB=1225 K.
P. 3606. Egy elektrolizáló kádhoz vezető függőleges, tömör rézvezetékben, melynek sugara 2 cm, 100 A erősségű áram folyik. Az áramvezető tengelyétől mekkora távolságban lesz az áram által keltett mágneses indukcióvektor nagysága 2.10-4 T?
(4 pont)
Közli: Holics László, Budapest
Megoldás. Két helyen is: a vezetéken kívül, annak tengelyétől 10 cm távolságban, illetve a vezeték belsejében, a tengelytől 4 mm távolságra.
P. 3607. Mekkora nyomást gyakorol a napfény március 22-én egy keletre néző ablakra reggel 6 órakor, ha a napfény 4%-át az ablak visszaveri, 6%-át elnyeli, a többit átengedi? Az ablakra érkező fény intenzitása 1000 W/m2.
(4 pont)
Közli: Részeg Anna, Budapest
Megoldás. 4,7.10-7 Pa. Ez az érték 11 nagyságrenddel (!) kisebb, mint a légköri nyomás, tehát közvetlen méréssel kimutathatatlan.
P. 3608. Egy \(\displaystyle \lambda\)0 hullámhosszúságú foton olyan elektronnal ütközik, amelynek pályája merőleges a foton mozgásirányára. A kölcsönhatás után az elektron megáll, a foton mozgásiránya pedig \(\displaystyle \vartheta\) szöggel megváltozik. Határozzuk meg \(\displaystyle \lambda\)0 és \(\displaystyle \vartheta\) értékét, ha a szórt foton hullámhossza \(\displaystyle \lambda\)0/2!
(5 pont)
Közli: Veres Zoltán, Margitta (Románia)
Megoldás. \(\displaystyle \vartheta\)=60o, \(\displaystyle \lambda\)0=2,42.10-12 m.
P. 3609. Hova lesz az összenyomott rugóban tárolt energia, ha a rugót ebben az állapotban sósavban feloldjuk?
(3 pont)
Közli: Kurucz Keve, Révkomárom (Szlovákia), Selye J. Gimn.
Megoldás. Az oldat belső energiáját (és ezzel együtt a hőmérsékletét) növeli.
P. 3610. A világ egyik legnagyobb gyémántja 44,5 karátos, csaknem tiszta szén. Minden szénatom 4 másikhoz kapcsolódik olyan kötésszögekkel, ahogy egy szabályos tetraéder középpontjából a csúcsok láthatók. Ha a kémiai kötéseket az atomok középpontjait összekötő kicsiny pálcikákkal szemléltetjük, és ezeket a pálcikákat gondolatban egy sorba rakjuk, milyen messze érne a gyémánt ilyen módon elrendezett vegyérték-láncolata?
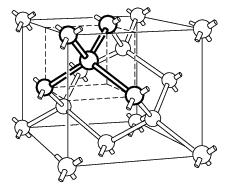
Útmutatás: A ,,gyémántszerkezet'' úgy is megkapható, hogy egy lapcentrált köbös kristályrácsot a testátló mentén az átló negyedrészével eltolva megismétlünk. (Lásd még a P. 3581. feladat megoldását lapunk 184. oldalán.)
(4 pont)
Közli: Gnädig Péter, Budapest
Megoldás. 1,4.1014 m. (Ez a távolság a Naprendszerünk méretének kb. 20-szorosa!)

