 |
A 2004. novemberi K-jelű matematika gyakorlatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
K. 13. Határozzuk meg a 71+72+...+72005 összeg utolsó két számjegyét.
Megoldás. Vegyük észre, hogy a 7 hatványainak utolsó két számjegye periodikusan ismétlődik: 07, 49, 43, 01, 07, .... A négy, ismétlődő végződés összege 00-ra végződik. Ha a 71+72+...+72005 összeg tagjait négyesével csoportosítjuk, akkor ennek megfelelően a négyes csoportokban lévő számok összegének utolsó két számjegye 00 lesz, tehát ezek összege is 00-ra végződik. Mivel 2005 4-gyel osztva 1-et ad maradékul, azért egyedül az utolsó tag nem kerül be ilyen négyes csoportba. Ez a korábban mondottak értelmében 07-re végződik, tehát az eredeti összeg is 07-re végződik.
K. 14. Alsóhuta, Felsőhuta és Középhuta között számos út vezet. Tudjuk azonban, hogy bármely két falu között a közvetlen utak száma legalább 3 és legfeljebb 10. Alsóhutáról Felsőhutára eljuthatunk közvetlenül, valamint Középhután keresztül is, összesen 33 különböző útvonalon. Hasonlóan Középhutáról Felsőhuta közvetlenül, valamint Alsóhuta érintésével is megközelíthető, összesen 23 különböző módon. Hány különböző útvonal vezet összesen Középhutáról Alsóhutára (közvetlenül, illetve Felsőhután keresztül)?
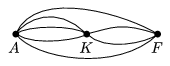
Példa: Az ábrán Alsóhutáról Felsőhutára 2 út vezet közvetlenül és 3.2=6 Középhután keresztül, ez összesen 8.
I. megoldás. Tekintsük a Középhuta és Felsőhuta közti 23 útvonalat. Ezek közül az Alsóhután keresztül menő útvonalakat úgy kapjuk meg, hogy összeszorozzuk a Közép- és Alsóhuta, valamint Alsó- és Felsőhuta közti közvetlen útvonalak számát. Ha táblázatba foglaljuk a lehetőségeket a Közép- és Felsőhuta között vezető közvetlen útvonalak száma szerint, akkor az alábbi értékeket kapjuk:
|
Közvetlen útvonalak száma Közép- és Felsőhuta között |
Alsóhután keresztülmenő útvonalak száma |
Alsó- és Felsőhuta közti közvetlen útvonalak száma |
Alsó- és Középhuta közti közvetlen útvonalak száma |
Alsó- és Felsőhuta közti összes útvonalak száma |
| x | 23-x=yz | y | z | y+xz |
| 3 | 20 | 4 | 5 | 4+15=19 |
| 3 | 20 | 5 | 4 | 5+12=17 |
| 4 | 19 | - | - | - |
| 5 | 18 | 3 | 6 | 3+30=33 |
| 5 | 18 | 6 | 3 | 6+15=21 |
| 6 | 17 | - | - | - |
| 7 | 16 | 4 | 4 | 4+28=32 |
| 8 | 15 | 3 | 5 | 3+40=43 |
| 8 | 15 | 5 | 3 | 5+24=29 |
| 9 | 14 | - | - | - |
| 10 | 13 | - | - | - |
A táblázat kitöltésénél figyelembe vettük, hogy semelyik két falu között nem mehet 10-nél több és 3-nál kevesebb út.
A szóba jöhető 7 lehetséges közvetlen útvonalszám esetén meg kell néznünk, hogy Alsóhuta és Felsőhuta között melyik esetben vezet összesen 33 út. A táblázat szerint ez csak egyszer teljesül. Ekkor Középhuta és Alsóhuta között összesen 6+15=21 különböző útvonal vezet.
II. megoldás. Jelöljük x-szel Alsóhuta és Felsőhuta, y-nal Középhuta és Felsőhuta, z-vel Középhuta és Alsóhuta között a közvetlen utak számát. Ekkor Alsóhutáról Felsőhutára összesen x+y.z különböző útvonalon lehet közlekedni. Hasonlóan Középhuta és Felsőhuta között y+x.z útvonalon, végül Középhuta és Alsóhuta között z+y.x útvonalon. Tudjuk, hogy x+y.z=33 és y+x.z= 23, a két egyenlet megfelelő oldalainak különbségét véve, és (y-x)-et kiemelve: (y-x).(z-1)=10. Mivel x, y, z egész számok, a 10-et kell két egész szorzatára bontani, és megvizsgálni, melyik elégíti ki a fenti két egyenletet. Felhasználva, hogy 3\(\displaystyle \le\)z\(\displaystyle \le\)10, csak két lehetőség marad z értékére: z=3, ekkor y-x=5; vagy z=6, ekkor y-x=2. Észrevehetjük továbbá, hogy z mindkét esetben osztható 3-mal, így az első egyenletből adódóan x-nek is oszthatónak kell lennie 3-mal. Ha z=3, akkor x értéke csak 3 lehet, mert ha legalább 6 lenne, akkor y már 10-nél több lenne. De a második egyenlet így sem teljesülhet, hiszen y már 14 lenne. Tehát z értéke csak 6 lehet. Ekkor az (x;y) számpár lehetséges értékei: (3;5) vagy (6;8). Az első számpár minden szempontból jónak bizonyul, a második viszont túl nagy akármelyik egyenlethez. Az egyetlen jó megoldás tehát: x=3, y=5, z=6, így z+y.x=21, azaz Alsóhutáról Középhutára 21 különböző útvonalon lehet eljutni.
K. 15. Az ABCD konvex négyszög A csúcsánál 100o-os szög van. Tudjuk, hogy az AC átló egy egyenlő oldalú és egy egyenlő szárú háromszögre osztja a négyszöget. Számítsuk ki a négyszög belső szögeinek nagyságát.
Megoldás. Az AC átló által levágott szabályos háromszög szögei 60 fokosak, ezért a másik, egyenlő szárú háromszög egyik szöge 40o. Ennek megfelelően két eset van: 40o a szárszög vagy az alapon fekvő szögek egyike (lásd az ábrákat).
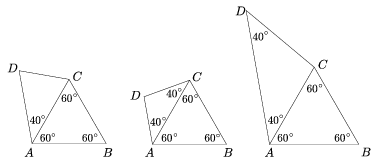
Az első esetben az egyenlő szárú háromszög alapon fekvő szögei 70 fokosak, így a négyszög belső szögeinek nagysága: 100o, 60o, 130o és 70o. A második esetben az egyenlő szárú háromszög szárszöge 100o, ami lehet az ACD háromszög D csúcsánál és lehet a C csúcsánál is. Ha a D csúcsnál lévő szög a 100 fokos, akkor a négyszög belső szögeinek nagysága: 100o, 60o, 100o, 100o. Ha pedig a C csúcsnál lévő szög a 100 fokos, akkor a négyszög belső szögeinek nagysága: 100o, 60o, 160o, 40o. Mindhárom esetben konvex négyszöget kaptunk.
K. 16. a) A 9, 8, 7, 6 számjegyek egyszeri felhasználásával alkossunk két darab kétjegyű számot úgy, hogy szorzatuk a lehető legnagyobb legyen.
b) A 9, 8, 7, 6, 5, 4 számjegyek egyszeri felhasználásával alkossunk három darab kétjegyű számot úgy, hogy szorzatuk a lehető legnagyobb legyen.
Indokoljuk is mindkét esetben, hogy miért a kapott számok lesznek a megfelelő számok.
Megoldás. a) A 9, 8, 7, 6 számokat párokba osztjuk, és az egy párban levő számokból képezzük a kétjegyű számokat. Nyilvánvaló, hogy ha a szorzat maximumát keressük, akkor úgy kell készítenünk a kétjegyű számokat, hogy az elöl álló számjegy nagyobb legyen, mint a hátul álló. Ennek megfelelően csak három lehetőség adódik:
| Egyik szám | Másik szám | Szorzat |
| 98 | 76 | 7448 |
| 97 | 86 | 8342 |
| 96 | 87 | 8352 |
A táblázatból leolvasható, hogy a keresett számpár a 96 és a 87.
b) A 9, 8, 7, 6, 5, 4 számokat párokba osztjuk, és az egy párban levő számokból képezzük a kétjegyű számokat. Nyilvánvaló, hogy ha a szorzat maximumát keressük, akkor úgy kell készítenünk a kétjegyű számokat, hogy az elöl álló számjegy nagyobb legyen, mint a hátul álló. Ennek megfelelően 15 lehetőség adódik:
| Első szám | Második szám | Harmadik szám | Szorzat |
| 98 | 76 | 54 | 402 192 |
| 98 | 75 | 64 | 470 400 |
| 98 | 74 | 65 | 471 380 |
| 97 | 86 | 54 | 450 468 |
| 97 | 85 | 64 | 527 680 |
| 97 | 84 | 65 | 529 620 |
| 96 | 87 | 54 | 451 008 |
| 96 | 85 | 74 | 603 840 |
| 96 | 84 | 75 | 604 800 |
| 95 | 87 | 64 | 528 960 |
| 95 | 86 | 74 | 604 580 |
| 95 | 84 | 76 | 606 480 |
| 94 | 87 | 65 | 531 570 |
| 94 | 86 | 75 | 606 300 |
| 94 | 85 | 76 | 607 240 |
A táblázatból leolvasható, hogy a 94, 85, 76 számhármas esetén lesz legnagyobb a szorzat.
K. 17. Az ABCD konkáv négyszög oldalai AB=13 cm, BC=4 cm, CD=3 cm, DA= 12 cm, a C csúcsnál lévő belső szöge pedig 270o. Mekkora a négyszög területe?
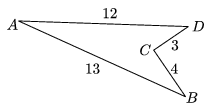
Megoldás. A BCD háromszög egy 3 és 4 befogójú derékszögű háromszög. Ennek harmadik oldala a Pitagorasz-tétel miatt 5 cm, területe pedig 6 cm2. Az ADB háromszög oldalaira teljesül, hogy a két kisebb oldal hosszának négyzetösszege egyenlő a legnagyobb oldalhossz négyzetével, így a Pitagorasz-tétel megfordítása szerint az ABD háromszög is derékszögű a D csúcsánál, tehát területe 30 cm2. A négyszög területe a két háromszög területének különbsége, azaz 24 cm2.
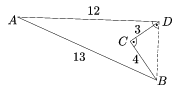
K. 18. Határozzuk meg az a, b, c és d különböző számjegyeket úgy, hogy \(\displaystyle \overline{abcd}:\overline{dcba}=4\), ahol \(\displaystyle \overline{abcd}\) és \(\displaystyle \overline{dcba}\) négyjegyű számokat jelöl.
Megoldás. A \(\displaystyle \overline{dcba}\) 4-szerese \(\displaystyle \overline{abcd}\), amely szintén négyjegyű, ezért \(\displaystyle \overline{dcba}<3000\), vagyis d értéke 1 vagy 2. De 1 nem lehet, mert akkor \(\displaystyle \overline{abcd}\) 1-re végződne, holott osztható 4-gyel. Így d=2, ekkor a=8 vagy 9, de ez utóbbinak a négyszerese nem 2-re végződik, tehát a=8. Mivel d négyszerese a, azért ha c-t szorozzuk 4-gyel, akkor nem lehet 10-es átlépés, eszerint csak c=1 vagy c=0 lehet. De \(\displaystyle \overline{abcd}\) osztható 4-gyel és a 02 végű szám nem osztható 4-gyel, ezért csak a c=1 lehet jó. Innen már adódik b=7 értéke. Vagyis a=8, b=7, c=1, d=2. A kapott szám a 8712, és ez valóban jó is.

