 Problem A. 578. (January 2013)
Problem A. 578. (January 2013)
A. 578. For every integer n 2 let P(n) be the product of all expressions of the form
2 let P(n) be the product of all expressions of the form where the signs of the terms are chosen arbitrarily.
(a) Prove that P(n) is a positive integer.
(b) Prove that for all 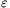 >0 there exists an n0 such that for every n>n0 the largest prime divisor of P(n) is smaller than
>0 there exists an n0 such that for every n>n0 the largest prime divisor of P(n) is smaller than .
(5 pont)
Deadline expired on February 11, 2013.
Statistics:
10 students sent a solution. 3 points: 2 students. 1 point: 8 students.
Problems in Mathematics of KöMaL, January 2013
