KöMaL Problems in Mathematics, January 2013
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 11, 2013. |
K. 361. A digital clock displays twelve noon in the form 12:00. Let us interpret that as a four-digit number: 1200. The intermediate times (displayed as hours and minutes) between twelve noon and midnight can all be interpreted in the same way as four-digit numbers. What is the sum of all such readings of four-digit numbers from 12:00 to 23:59?
(6 pont)
solution (in Hungarian), statistics
K. 362. Peter takes 5 hours to do a certain job alone, and Paul takes 6 hours to do the same job alone. When they work together, they are both behindered by their continual quarrelling about everything, and their productivity decreases: each of them will do the work at a rate lowered by the same percentage. By what percentage is it lowered if the two of them take 3.5 hours to finish the job together?
(6 pont)
solution (in Hungarian), statistics
K. 363. Big Ben announces every hour by as many strikes as the number of hours. When the clock has struck, the sound is heard a little time longer, and there are pauses between the sounds heard. Given that Big Ben takes 9 seconds to strike 3 and that it takes 10.5 seconds longer to strike 5 than to strike 2, calculate the total time, in seconds, of the sound of the strikes being heard during a day.
(6 pont)
solution (in Hungarian), statistics
K. 364. One edge of a rectangular block of wood measures 10 cm. Three pairwise perpendicular bores, each of 2 cm by 2 cm square cross section, parallel to edges, are made through the block. (The three bores do not meet.) With the first bore made, the surface area of the block grew by 32 cm2. The second bore further increased the surface area by 15.92%. The third bore was made parallel to the 10-cm edge. What was the remaining volume of the block after all three bores being made?
(6 pont)
solution (in Hungarian), statistics
K. 365. D is a point on the extension of side AC of a regular triangle ABC beyond vertex A. The distance of point D from line AB is 4, and its distance from line BC is 10. Find the area of triangle ABC.
(6 pont)
solution (in Hungarian), statistics
K. 366. What is the largest score that is impossible to achieve with the dart board shown, no matter how many darts are thrown?
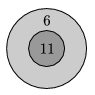
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 11, 2013. |
C. 1150. A square made up of an odd number of small squares is drawn on squared paper. We want to draw a closed polygon along grid lines such that it passes through every lattice point in the interior or on the boundary of the large square exactly once, and it does not leave the large square. Express the length of the polygon in terms of the length of the side of the large square.
(5 pont)
solution (in Hungarian), statistics
C. 1151. An arbitrary interior point P of a convex quadrilateral ABCD is connected to the midpoints E, F, G, H of the sides AB, BC, CD, DA, respectively. Prove that the sum of the areas of the quadrilaterals AEPH and CGPF is equal to the sum of the areas of the quadrilaterals BFPE and DHPG. (Any of them may be a degenerate quadrilateral.)
Suggested by R. Gyimesi, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1152. Let and let
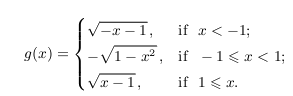
Find the zeros of f-g.
(5 pont)
solution (in Hungarian), statistics
C. 1153. A square of unit diagonal is cut along one of the diagonals, and the two parts are moved towards each other along the line of the other diagonal. What is the maximum possible area of the overlapping region?
(5 pont)
solution (in Hungarian), statistics
C. 1154. Is there an arithmetic progression in which the sum of the first n terms is n, the sum of the first 2n terms is n2, and the sum of the first 3n terms is n3?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 11, 2013. |
B. 4502. There are 2013 discs in a sack, numbered from 1 to 2013. How many discs need to be drawn without replacement to be certain that there will be two among them with numbers that add up to a multiple of 7?
Suggested by D. Fülöp, Pécs
(3 pont)
solution (in Hungarian), statistics
B. 4503. Find all four-digit perfect squares in which the first two digits are equal and the last two digits are also equal.
(3 pont)
solution (in Hungarian), statistics
B. 4504. In a right-angled triangle, the segment of the perpendicular bisector of the hypotenuse between the lines of the legs is equal in length to the hypotenuse. Determine the angles of the triangle.
(4 pont)
solution (in Hungarian), statistics
B. 4505. We have two containers with volumes of p litres and of q litres. It is allowed to fill up completely or empty either container at a tap, to fill up either container completely from the other one, and to pour the entire content of one into the other. Prove that if p>q are relatively prime positive integers, and s is a positive integer such that s p, then it is possible to achieve that one container have exactly s litres of water in it.
p, then it is possible to achieve that one container have exactly s litres of water in it.
Suggested by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4506. Prove that there exists a set of infinitely many positive integers such that no finite subset of them add up to a perfect square.
Suggested by P. Kutas, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4507. The area of a regular heptagon is 4095 units. A and B are two consecutive vertices, and K is the centre of the heptagon. P is a point lying on the circumscribed circle of triangle ABK in the interior of the heptagon. Given that , what may be the area of triangle ABP?
Italian competition problem
(5 pont)
solution (in Hungarian), statistics
B. 4508. Show that if a, b and c are positive numbers then .
Inspired by Jim Boyd, USA
(4 pont)
solution (in Hungarian), statistics
B. 4509. The axes of two parabolas are perpendicular to each other. Show that the intersections of the two curves lie on a circle.
Suggested by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4510. The length of the base edges of a right regular pyramid of (2k+1) sides is 1, the centre of the base is O, and the length of the altitude OB is m. The pyramid is reflected in the midpoint of OB. Find the volume of the intersection of the two pyramids.
(6 pont)
solution (in Hungarian), statistics
B. 4511. The circle k touches the circle  internally at point P. A line p passing through P intersects the circles again at the points K and L, respectively. u is the tangent drawn at a point U of circle k. One intersection of u with the circle
internally at point P. A line p passing through P intersects the circles again at the points K and L, respectively. u is the tangent drawn at a point U of circle k. One intersection of u with the circle  is V, and the intersection of lines KU and LV is T. Determine the locus of the point T as U traverses the circle k. (Consider both intersections of u and
is V, and the intersection of lines KU and LV is T. Determine the locus of the point T as U traverses the circle k. (Consider both intersections of u and  ; if U=K, the line KU is the tangent to k at K. Analogously, if V=L then LV is the tangent drawn to
; if U=K, the line KU is the tangent to k at K. Analogously, if V=L then LV is the tangent drawn to  at L.)
at L.)
Suggested by A. Hraskó, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 11, 2013. |
A. 578. For every integer n 2 let P(n) be the product of all expressions of the form
2 let P(n) be the product of all expressions of the form where the signs of the terms are chosen arbitrarily.
(a) Prove that P(n) is a positive integer.
(b) Prove that for all  >0 there exists an n0 such that for every n>n0 the largest prime divisor of P(n) is smaller than
>0 there exists an n0 such that for every n>n0 the largest prime divisor of P(n) is smaller than .
(5 pont)
A. 579. The circle k1 is internally tangent to the circle k which is externally tangent to k2. The common external tangents of k1 and k2 are u and v. The line u is tangent to k1 and k2 at P and Q, respectively, and meets k at A and B in such a way that B lies between P and Q. Analogously, the line v is tangent to k1 and k2 at R and S, respectively, and meets k at C and D in such a way that D lies between R and S and k1 is tangent to that arc BD of k which does not contain A and C.
Show that
(5 pont)
solution (in Hungarian), statistics
A. 580. Show that for every positive integer k and real number  >0 there exists a polynomial p(x)=xn+an-1xn-1+...+a1x+a0 with real coefficients such that p(x) is divisible by the polynomial (x-1)k+1 and
>0 there exists a polynomial p(x)=xn+an-1xn-1+...+a1x+a0 with real coefficients such that p(x) is divisible by the polynomial (x-1)k+1 and
(5 pont)
Upload your solutions above.
