Problem A. 579. (January 2013)

A. 579. The circle k₁ is internally tangent to the circle k which is externally tangent to k₂. The common external tangents of k₁ and k₂ are u and v. The line u is tangent to k₁ and k₂ at P and Q, respectively, and meets k at A and B in such a way that B lies between P and Q. Analogously, the line v is tangent to k₁ and k₂ at R and S, respectively, and meets k at C and D in such a way that D lies between R and S and k₁ is tangent to that arc BD of k which does not contain A and C.

Show that

(5 pont)

Deadline expired on February 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Legyen az ABD és CBD háromszögek beírt köreinek középpontja I_A, illetve I_C, továbbá legyen ugyanezekben a háromszögekben a BD oldalhoz hozzáírt körök középpontja J_A, illetve I_C.

Lemma. A PR szakasz átmegy az I_A és I_C pontokon, továbbá a QS egyenes átmegy a J_A és J_C pontokon.

A lemma első fele (a beírt körökre vonatkozó állítás) Sawayama-lemma néven ismert. Egy-egy bizonyítása megtalálható például az A. 505. feladat megoldásában vagy itt vagy itt. Az Olvasóra bízzuk annak végiggondolását, hogy a bizonyításokat hogyan lehet átírni hozzáírt körökre.

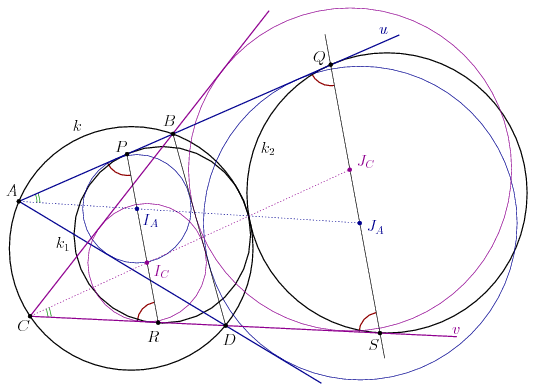
Jól ismert (és például az ABI_A és AJ_AD háromszögek hasonlóságából könnyen igazolható), hogy

AB^.AD=AI_A^.AJ_A,

és ugyanígy

CB^.CD=CI_C^.CJ_C.

Az AI_AP, AJ_AQ, CI_CR és CJ_CS háromszögek hasonlók, mert PR és QS párhuzamos. Ezért

Így

Statistics:

2 students sent a solution.
5 points:	Cyril Letrouit.
3 points:	1 student.

Problems in Mathematics of KöMaL, January 2013