 Problem A. 580. (January 2013)
Problem A. 580. (January 2013)
A. 580. Show that for every positive integer k and real number 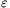 >0 there exists a polynomial p(x)=xn+an-1xn-1+...+a1x+a0 with real coefficients such that p(x) is divisible by the polynomial (x-1)k+1 and
>0 there exists a polynomial p(x)=xn+an-1xn-1+...+a1x+a0 with real coefficients such that p(x) is divisible by the polynomial (x-1)k+1 and
(5 pont)
Deadline expired on February 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Az A. 574. feladat megoldásában a Tk(x) Csebisev-polinom abszolút értékét 1-gyel becsültük azalakú helyeken, ahol 0
n-1 egész szám volt:
Ez a becslés csak akkor lehet éles, ha
közel az +1 vagy -1 pontokhoz, vagy pedig a Tk valamelyik lokális szélsőértékéhez, ahol Tk(x) értéke szintén
1 (ez összesen k+1 pont a [-1,1] intervallumban), vagy pedig
kicsi, például 0.
A feladat megoldásához egy "ritka" polinomot fogunk konstruálni, aminek összesen csak k+2 nemnulla együtthatója van. (A polinom foka sokkal nagyobb lesz, mint k.)
Megoldás. Fel fogjuk használni az A. 574. feladat megoldásának több elemét, így a következő lemmát:
1. lemma. Ha a polinom osztható az (x-1)k+1 polinommal, akkor tetszőleges, legfeljebb k-adfokú q(y) polinomra
(A lemma bizonyítása megtalálható az A. 574. feladat megoldásánál.)
Legyen k és 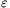 >0 rögzített; ezekhez szeretnénk a p polinomot megkonstruálni. Legyen
>0 rögzített; ezekhez szeretnénk a p polinomot megkonstruálni. Legyen 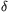 >0 és n egy nagy pozitív egész; ezeket majd később definiáljuk.
>0 és n egy nagy pozitív egész; ezeket majd később definiáljuk.
Legyenek azok a pontok, ahol a Tk Csebisev-polinom értéke
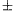 1: ekkor Tk(ui)=(-1)k-i. (Könnyű ellenőrizni, hogy
1: ekkor Tk(ui)=(-1)k-i. (Könnyű ellenőrizni, hogy , de erre a képletre nem lesz szükség.) Minden
-ra legen di az (az egyik) nemnegatív egész szám, ami a legközelebb van
számhoz, azaz
Ha
| (1) |
akkor a di értékek különbözők: . Ezen kívül legyen dk+1=n. A p(x) polinomot a következő alakban keressük:
avagy, adi=bi, és minden indexre ai=0.
2. lemma. (a) A valós számokat meg lehet választani úgy, hogy ne legyen mindegyikük nulla, és a p(x) polinom osztható legyen (x-1)k+1-gyel.
(b) A számok egyike sem lehet nulla, és a
sorozat biztosan váltakozó előjelű.
Bizonyítás. (a) Legyen minden 0 i
i k+1-re az xdi polinom osztási maradéka ri(x). Ez összesen k+2 polinom, mindegyikük foka legfeljebb k. Ezért a maradékok lineárisan összefüggnek: alkalmas
k+1-re az xdi polinom osztási maradéka ri(x). Ez összesen k+2 polinom, mindegyikük foka legfeljebb k. Ezért a maradékok lineárisan összefüggnek: alkalmas számokkal, amelyek nem miond nullák,
.
(b) Tegyük fel indirekte, hogy a sorozat nem váltakozó előjelű: valamelyik j indexre bj és bj+1 azonos előjelű, vagy egyikük 0. Lehetséges, hogy vannak szomszédos nulla értékek a sorozatban; olyan j-t válasszunk, amikor bj és bj+1 valamelyike nem nulla.
Legyen . Ez egy k-adfokú polinom, amire alkalmazhatjuk az 1. lemmát:
A baloldalon kettő kivétellel minden tagban h(di)=0. A maradék két tagban h(dj) és h(dj+1) egyike sem nulla, és azonos előjelű. A bj és bj+1 együtthatók szintén azonos előjelűek, és nem mindettő nulla. Az összegben tehát egy vagy két, azonos előjelű nemnulla tag van, így az összeg nem lehet nulla, ellentmondás. Ezzel a lemmát igazoltuk.
(Megjegyzés. Az is igaz, hogy a p(x) polinom konstans szorzótól eltekintve egyértelmű, de erre szintén nem lesz szükségünk.)
Most már van egy p(x) polinomunk, ami osztható a (x-1)k+1 polinommal. A p(x) polinomot végigosztva bk+1-gyel elérhetjük, hogy an=bk+1=1 legyen. A váltakozó előjel miatt ekkor pozitív,
pedig negatív lesz.
Az A. 574. feladat hasonlóan legyen
Az 1. lemma szerint
avagy, átrendezve,
| (*) |
A di számokat azért választottuk így, hogy q(di) "közel" legyen (-1)k-i-hez. Ezt most pontosabban megbecsüljük.
Az i=0 és i=k esetekben q(d0)=q(0)=Tk(-1)=(-1)k, illetve q(dk)=q(n-1)=Tk(1)=1.
Minden 1 i
i k-1-re a Tk polinomnak lokális szélsőértéke van az ui helyen, ezért Tk'(ui)=0. Ezért van olyan
k-1-re a Tk polinomnak lokális szélsőértéke van az ui helyen, ezért Tk'(ui)=0. Ezért van olyan 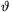 i>0 szám, hogy 1
i>0 szám, hogy 1 i
i k-1 és |x-ui|<
k-1 és |x-ui|<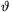 i esetén |Tk(x)-Tk(ui)|<
i esetén |Tk(x)-Tk(ui)|<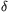 |x-ui|. Ha n-et olyan nagynak választjuk, hogy
|x-ui|. Ha n-et olyan nagynak választjuk, hogy
| (2) |
akkor
és
Ha
n>1+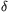 , , | (3) |
akkor |q(di)-(-1)k-i|<1 minden i-re, ezért sorozat váltakozó előjelű, és
Még szükségünk lesz q(dk+1)=q(n) felső becslésére is. Az A. 574. feladat megoldásából is tudjuk, hogy Tk(1)=1 és Tk'(1)=k2. Ezért van olyan 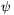 >0, hogy 1
>0, hogy 1 x
x 1+
1+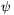 esetén Tk(x)<1+(1+
esetén Tk(x)<1+(1+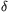 )k2(x-1). Ha
)k2(x-1). Ha
| (4) |
akkor tehát
Az (*) azonosság baloldalát alulról, a jobboldalt felülről becsüljük. A baloldalon minden tag pozitív, ezért
illetve
Tehát
Már csak a feladatbeli alakra kell rendeznünk ezt a becslést.
Válasszuk 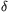 -t olyan kicsinek, hogy
-t olyan kicsinek, hogy
teljesüljön, például legyen
Ezután válasszuk n-et olyan nagynak, hogy
is érvényes legyen. Ezt is elérhetjük, ha
| (5) |
Ekkor tehát
A becsléseink akkor érvényesek, ha (1)-(5) mindegyike teljesül. Ez csak véges sok, csak a k-tól függő alsó korlát az n-re.
Statistics:
0 student sent a solution.
Problems in Mathematics of KöMaL, January 2013

