 |
A B. 4780. feladat (2016. március) |
B. 4780. Határozzuk meg azokat az \(\displaystyle n\) természetes számokat, melyekre igaz, hogy ha egy \(\displaystyle \mathcal{K}_n\) konvex \(\displaystyle n\)-szög oldalfelezőpontjai szabályos \(\displaystyle n\)-szöget alkotnak, akkor \(\displaystyle \mathcal{K}_n\) maga is szabályos \(\displaystyle n\)-szög.
(4 pont)
A beküldési határidő 2016. április 11-én LEJÁRT.
Megoldásvázlat. Belátható, hogy az \(\displaystyle 1\)-nél nagyobb páratlan \(\displaystyle n\)-ek lesznek a megfelelőek.
Ha \(\displaystyle n\geq 3\) páratlan szám, akkor a felezőpontokból egyértelműen megszerkeszthető a \(\displaystyle \mathcal{K}_{n}\) sokszög.
Vegyünk egy tetszőleges \(\displaystyle P\) pontot és tükrözzük rendre a megadott oldalfelező pontokra. Páratlan sok középpontos tükrözés egymásutánja is középpontos tükrözés, így a végül kapott \(\displaystyle P_{n}\) pontból a \(\displaystyle P_{n}P\) felezőpontjaként a tükrözés fixpontja - a sokszög egyik csúcsa - adódik. Ezután ezt a pontot az előbbi sorrendben rendre tükrözve a felezőpontokra megkapjuk a sokszög összes csúcsát.
Ez pedig azt jelenti, hogy egy felezőponti \(\displaystyle n\)-szöghöz pontosan egy \(\displaystyle \mathcal{K}_{n}\) tartozhat. Tudjuk, hogy egy szabályos \(\displaystyle n\)-szög felezőpontjai szabályos \(\displaystyle n\)-szöget alkotnak, azért ezekből már következik, hogy a páratlan számok valóban megfelelőek.
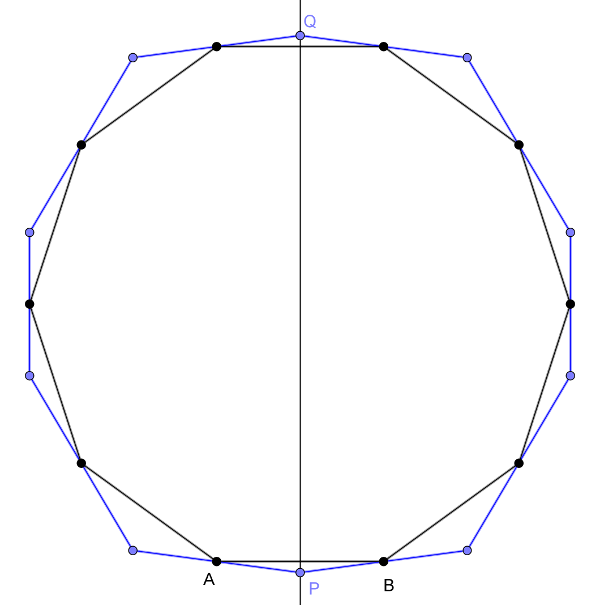
Páros sok pont esetén nem igaz az állítás. Tekintsük a felezőpontokból álló szabályos sokszög \(\displaystyle AB\) oldalának felezőmerőlegesét, és ezen egy megfelelő \(\displaystyle P\) pontot. Ezt tükrözzük sorban a felezőpontokra az \(\displaystyle A\), illetve a \(\displaystyle B\) pont irányában elindulva. A szimmetria miatt mindkét irányban a \(\displaystyle Q\) ponthoz jutunk. A kapott kék sokszög az eredeti sokszög, ami nem feltétlenül szabályos.
Statisztika:
68 dolgozat érkezett. 4 pontot kapott: Baran Zsuzsanna, Bindics Boldizsár, Borbényi Márton, Cseh Kristóf, Csiszár Zoltán, Döbröntei Dávid Bence, Fajszi Bulcsú, Fuisz Gábor, Fülöp Anna Tácia, Gáspár Attila, Glasznova Maja, Hansel Soma, Hornák Bence, Imolay András, Janzer Orsolya Lili, Kerekes Anna, Klász Viktória, Kocsis Júlia, Kovács 246 Benedek, Matolcsi Dávid, Molnár-Sáska Zoltán, Nagy Dávid Paszkál, Nagy Kartal, Németh 123 Balázs, Németh 417 Tamás, Radnai Bálint, Sal Kristóf, Schrettner Bálint, Schrettner Jakab, Szabó 417 Dávid, Szemerédi Levente, Váli Benedek, Varsányi András. 3 pontot kapott: 20 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2016. márciusi matematika feladatai

