 |
A B. 4878. feladat (2017. május) |
B. 4878. Legfeljebb mekkora lehet a \(\displaystyle PA+PB+PC+PD\) összeg, ha \(\displaystyle P\) az \(\displaystyle ABCD\) egységnégyzet egy pontja?
(4 pont)
A beküldési határidő 2017. június 12-én LEJÁRT.
Megoldásvázlat. Felhasználjuk a következő ismert állítást: Ha \(\displaystyle P\) az \(\displaystyle XYZ\triangle\) egy (nem feltétlen belső) pontja, akkor \(\displaystyle PX+PY\le ZX+ZY\), és egyenlőség csak \(\displaystyle P=Z\) esetben áll. (Lásd például Horvay-Reiman: Geometriai feladatok gyűjteménye I, 172. feladat.)
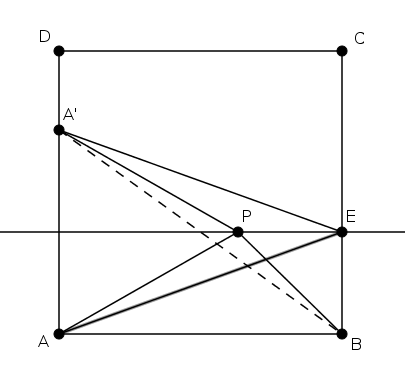
Az általánosság megszorítása nélkül feltehetjük, hogy \(\displaystyle PA\geq PB\). A \(\displaystyle P\)-n keresztül \(\displaystyle AB\)-vel húzott \(\displaystyle e\) párhuzamos messe \(\displaystyle BC\)-t \(\displaystyle E\)-ben, és legyen \(\displaystyle A\) tükörképe \(\displaystyle e\)-re \(\displaystyle A'\). Alkalmazzuk a fenti segédállítást \(\displaystyle A'BE\triangle\)-ben \(\displaystyle P\) pontra, így a tükrözés miatt \(\displaystyle PA+PB=PA'+PB\leq EA'+EB= EA+EB\), és egyenlőség csak \(\displaystyle E=P\)-re áll. Mivel a \(\displaystyle CD\) oldalra hasonlóan indokolhatunk, így kaptuk, hogy \(\displaystyle PA+PB+PC+PD\le EA+EB+EC+ED\), és egyenlőség csak \(\displaystyle P=E\) esetén állhat.
Ismét az általánosság megszorítása nélkül \(\displaystyle EC\ge EB\). Mivel \(\displaystyle E\) rajta van a \(\displaystyle BC\) oldalon, így \(\displaystyle EB+EC=BB+BC\). \(\displaystyle EA+ED\leq BA+BD\) pedig pontosan ugyanúgy igazolható, ahogy \(\displaystyle PA+PB\leq EA+EB\)-t megmutattuk. Tehát \(\displaystyle EA+EB+EC+ED\leq BA+BB+BC+BD\), és egyenlőség csak akkor áll, ha \(\displaystyle E=B\).
Ezzel megmutattuk, hogy \(\displaystyle PA+PB+PC+PD\) pontosan akkor maximális, ha \(\displaystyle P\) valamelyik csúcs, a maximum értéke pedig \(\displaystyle 2+\sqrt 2\).
Statisztika:
58 dolgozat érkezett. 4 pontot kapott: Baran Zsuzsanna, Beke Csongor, Borbényi Márton, Csiszár Zoltán, Daróczi Sándor, Deák Bence, Fekete Balázs Attila, Fülöp Anna Tácia, Gáspár Attila, Hervay Bence, Imolay András, Janzer Orsolya Lili, Kerekes Anna, Kiss Gergely, Kocsis Anett, Kővári Péter Viktor, Lakatos Ádám, Márton Dénes, Mikulás Zsófia, Németh 123 Balázs, Noszály Áron, Olosz Adél, Póta Balázs, Scheidler Barnabás, Schrettner Jakab, Sebestyén Pál Botond, Simon Dániel Gábor, Soós 314 Máté, Sulán Ádám, Szabó 417 Dávid, Szakály Marcell, Tiderenczl Dániel, Tóth-Rohonyi Iván, Török Tímea, Török Zsombor Áron, Velkey Vince, Zsigri Bálint. 3 pontot kapott: Csahók Tímea, Füredi Erik Benjámin, Kovács 654 Áron , Szabó Kristóf, Szemerédi Levente, Szőnyi Laura, Varsányi András. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. májusi matematika feladatai

