 |
A C. 1083. feladat (2011. május) |
C. 1083. Egy háromszög egyik oldalának hossza 8 cm, a rajta fekvő egyik szög 60o-os, a háromszögbe írható kör sugara pedig cm. Mekkora a háromszög másik két oldala?
(5 pont)
A beküldési határidő 2011. június 10-én LEJÁRT.
Megoldás.
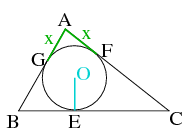
Az \(\displaystyle ABC\) háromszög beírt köre az oldalakat az \(\displaystyle E\), \(\displaystyle F\) és \(\displaystyle G\) pontokban érinti. A \(\displaystyle BEO\) derékszögű háromszög egyik befogója \(\displaystyle \sqrt 3\) hosszú, a vele szemközti szög pedig \(\displaystyle 30^\circ\), ezért \(\displaystyle BE=\sqrt 3 \cdot \ctg 30^\circ =3=BG\). Az \(\displaystyle ABC\) háromszög területének kétszerese a beírt kör sugarának segítségével \(\displaystyle 2t=(8+CF+x+x+GB)\cdot \sqrt 3 =(16+2x)\cdot \sqrt 3\), másrészről két oldalának és a közrezárt szög segítségével \(\displaystyle 2t=8(3+x)\cdot \sin 60^\circ.\) E kettő egyenlőségéből \(\displaystyle 16+2x=4(3+x)\), ahonnan \(\displaystyle x=2\). A háromszög oldalai tehát \(\displaystyle AB=3+2=5\)cm és \(\displaystyle CA=8-3+2=7\)cm.
Statisztika:
101 dolgozat érkezett. 5 pontot kapott: 55 versenyző. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 38 versenyző. 2 pontot kapott: 2 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2011. májusi matematika feladatai

