 Problem C. 1119. (March 2012)
Problem C. 1119. (March 2012)
C. 1119. Two identical set squares(of 30, 60 and 90 degrees) are fixed together along their shorter legs of length 10 cm, as shown in the figure. Then an isosceles set square is placed on top. Is there enough room for a tennis ball of radius 3.2 cm in the interior of the tetrahedron obtained in this way?
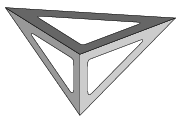
(5 pont)
Deadline expired on April 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az egyenlő szárú derékszögű vonalzó befogójának hossza \(\displaystyle \frac{\sqrt 3}2 \cdot 10\) cm hosszú, a vonalzók alkotta tetraéder térfogata pedig \(\displaystyle \frac{1}{6}\cdot 10\cdot 10\cdot \frac{\sqrt 3}2 \cdot 10=\frac{1000\sqrt 3}{12}cm^3\approx 144,3cm^3\). A tetraéderbe írható gömb sugara \(\displaystyle r\), akkor a térfogata kiszámolható \(\displaystyle \frac{1}{3}A\cdot r\)-ként is. A vonalzók alkotta tetraéder negyedik lapjának oldalai \(\displaystyle 20cm\), \(\displaystyle 20cm\) és \(\displaystyle \frac{\sqrt 6}2 \cdot 10 cm\) hosszúak, területe (pl. Heron-képletet alkalmazva) \(\displaystyle \frac{25\sqrt{15}}{2}cm^2\). A felszín tehát \(\displaystyle A=\frac{\sqrt 3}{8}\cdot 100 + \frac{\sqrt 3}{4}\cdot 100 + \frac{3}{8}\cdot 100 + \frac{\sqrt{15}}{8}\cdot 100 \approx 172,5 cm^2\). A tetraéderbe írható gömb sugara tehát \(\displaystyle r\approx 3,58 cm\), vagyis belefér a vonalzók alkotta tetraéderbe egy 3,2 cm sugarú teniszlabda.
Statistics:
156 students sent a solution. 5 points: 90 students. 4 points: 12 students. 3 points: 26 students. 2 points: 12 students. 1 point: 5 students. 0 point: 7 students. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, March 2012
