Problem C. 1151. (January 2013)

C. 1151. An arbitrary interior point P of a convex quadrilateral ABCD is connected to the midpoints E, F, G, H of the sides AB, BC, CD, DA, respectively. Prove that the sum of the areas of the quadrilaterals AEPH and CGPF is equal to the sum of the areas of the quadrilaterals BFPE and DHPG. (Any of them may be a degenerate quadrilateral.)

Suggested by R. Gyimesi, Budapest

(5 pont)

Deadline expired on February 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A \(\displaystyle P\) pontot kössük össze a négyszög csúcsaival és az oldalak felezőpontjával. Ekkor nyolc háromszöget kapunk. Mivel az \(\displaystyle ABP\), a \(\displaystyle BCP\), a \(\displaystyle CDP\) és a \(\displaystyle DAP\) háromszögben \(\displaystyle PE\), \(\displaystyle PF\), \(\displaystyle PG\) és \(\displaystyle PH\) súlyvonalak, ezért két-két megfelelő háromszög területe egyenlő.

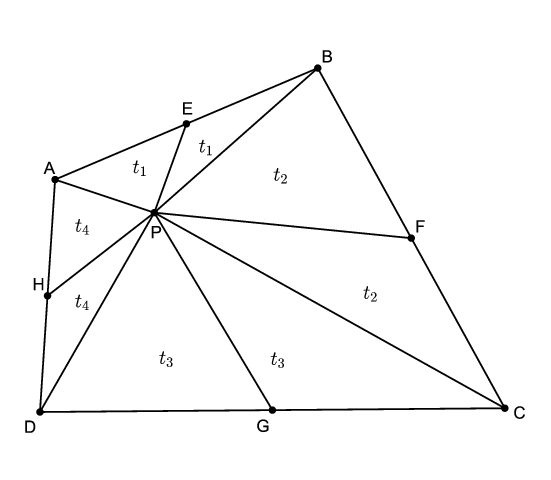
Ezt felhasználva:

\(\displaystyle t_{AEPH}+t_{CGPF}=(t_1+t_4)+(t_3+t_2)=(t_2+t_1)+(t_4+t_3)=t_{BFPE}+t_{DHPG}.\)

Statistics:

222 students sent a solution.
5 points:	154 students.
4 points:	43 students.
3 points:	10 students.
2 points:	7 students.
1 point:	3 students.
0 point:	3 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, January 2013