 Problem C. 1153. (January 2013)
Problem C. 1153. (January 2013)
C. 1153. A square of unit diagonal is cut along one of the diagonals, and the two parts are moved towards each other along the line of the other diagonal. What is the maximum possible area of the overlapping region?
(5 pont)
Deadline expired on February 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Egy egységnyi átlójú négyzet területe 1/2. Az \(\displaystyle ABCD\) négyzetet a \(\displaystyle BD\) átlója mentén kettévágva, az \(\displaystyle ABD\) háromszöget az \(\displaystyle A'B'D'\) háromszögbe toljuk el. Jelölje a \(\displaystyle DE\) szakasz hosszát \(\displaystyle y>0\). Ha \(\displaystyle y=DC/2\), akkor a közös rész pont a négyzet negyede, vagyis területe \(\displaystyle 1/8\). Ha még tovább toljuk a háromszöget, vagyis \(\displaystyle y>DC/2\), akkor a közös rész területe ennél kisebb lesz. Legyen \(\displaystyle y<DC/2\).
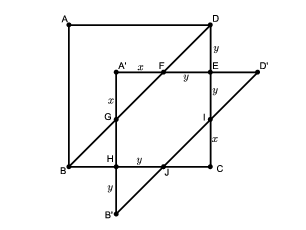
Az eltolás miatt ekkor \(\displaystyle HB'=DE=y\). Mivel a \(\displaystyle DEF\) és a \(\displaystyle HB'J\) háromszögek derékszögűek, és két másik szögük \(\displaystyle 45^{\circ}\)-os, ezért egyenlő szárúak, és így \(\displaystyle EF=HJ=y\). A szimmetria miatt ekkor \(\displaystyle EI=HJ=y\). Az \(\displaystyle AC\)-re való szimmetria miatt ekkor \(\displaystyle EI=HJ=y\) és \(\displaystyle GH=FE=y\).
Legyen az \(\displaystyle A'F\) szakasz hossza \(\displaystyle x\). Ekkor a fentiekhez hasonlóan \(\displaystyle A'G=x\) is teljesül. Vagyis \(\displaystyle A'B'=x+y+y=x+2y\). Mivel \(\displaystyle A'B'=DC\), így \(\displaystyle DC=x+2y\), amiből \(\displaystyle IC=x\).
Most már felírhatjuk a kérdéses területet. Ehhez felhasználjuk, hogy a négyzet oldalának hossza \(\displaystyle \frac{\sqrt2}{2}=x+2y\), amiből \(\displaystyle y=\frac{\sqrt2}{4}-\frac x2\).
\(\displaystyle t=t_{BCD}-t_{IJC}-2\cdot t_{DEF}=\frac14-\frac{x^2}{2}-2\cdot\frac{y^2}{2}=\)
\(\displaystyle =\frac14-\frac{x^2}{2}-\left(\frac{\sqrt2}{4}-\frac x2\right)^2=-\frac34x^2+\frac{\sqrt2}{4}x+\frac18=\)
\(\displaystyle =-\frac34\left(\left(x-\frac{\sqrt2}{6}\right)^2-\frac{8}{36}\right).\)
Tehát a terület \(\displaystyle x=\frac{\sqrt2}{6}\) esetén lesz a legnagyobb, értéke ekkor \(\displaystyle -\frac34\cdot\left(-\frac{8}{36}\right)=\frac16\).
Statistics:
178 students sent a solution. 5 points: 92 students. 4 points: 29 students. 3 points: 8 students. 2 points: 9 students. 1 point: 18 students. 0 point: 20 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, January 2013
