 |
A C. 1344. feladat (2016. március) |
C. 1344. Mutassuk meg, hogy a kilenc oldalú szabályos sokszögekben a legnagyobb és legkisebb átló hossza közötti különbség éppen a sokszög oldalának hosszával egyenlő.
(5 pont)
A beküldési határidő 2016. április 11-én LEJÁRT.
1. megoldás. Legyen a leghosszabb átló hossza \(\displaystyle f\), a legrövidebbé \(\displaystyle e\), végül a sokszög oldalának hossza \(\displaystyle x\). Tekintsünk egy \(\displaystyle e\) és egy \(\displaystyle f\) hosszúságú átlót, melyek egymással párhuzamosak, az ábra szerint. A szimmetria miatt \(\displaystyle AC||ID\) és \(\displaystyle ACDI\) szimmetrikus trapéz. A szabályos kilencszög szögeinek nagysága \(\displaystyle 7\cdot180^{\circ}/9=140^{\circ}\), tehát \(\displaystyle IAB\angle=ABC\angle=BCD\angle=140^{\circ}\). Az \(\displaystyle ABC\) egyenlő szárú háromszögben így az alapon fekvő szögek nagysága \(\displaystyle BAC\angle=BCA\angle=40^{\circ}/2=20^{\circ}\). Tehát \(\displaystyle IAC\angle=DCA\angle=140^{\circ}-20^{\circ}=120^{\circ}\), és így az \(\displaystyle IACD\) trapéz \(\displaystyle ID\) alapon fekvő szögeinek nagysága \(\displaystyle 180^{\circ}-120^{\circ}=60^{\circ}\). Húzzunk az \(\displaystyle A\) csúcson keresztül párhuzamost a \(\displaystyle CD\) szárral, ennek és az \(\displaystyle ID\) oldalnak a metszéspontja legyen \(\displaystyle J\) (1. ábra).
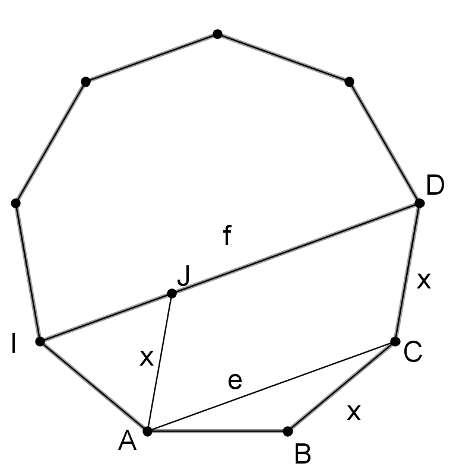
1. ábra
A párhuzamosság miatt az \(\displaystyle ACDJ\) négyszög paralelogramma, így egyrészt \(\displaystyle JA=DC=x\) és \(\displaystyle JD=AC=e\), másrészt \(\displaystyle IJA\angle=IDC\angle=60^{\circ}\), tehát az \(\displaystyle IJA\) háromszögben \(\displaystyle IJA\angle=JIA\angle=60^{\circ}\), a háromszög szabályos, oldalainak hossza \(\displaystyle x\). Másrészt \(\displaystyle IJ=ID-JD=f-e\). Tehát \(\displaystyle x=f-e\), és ezt kellett belátni.
2. megoldás. Ismeretes, hogy \(\displaystyle r\) sugarú körben, ha a \(\displaystyle h\) húrhoz tartozó középponti szög \(\displaystyle \alpha\), akkor \(\displaystyle h=2r\sin\frac{\alpha}{2}\).
A szabályos kilencszögben az oldalhoz tartozó középponti szög nagysága \(\displaystyle 40^{\circ}\), a legrövidebb átlóhoz tartozóé \(\displaystyle 80^{\circ}\), a leghosszabbhoz tartozóé pedig \(\displaystyle 160^{\circ}\).
Így a 2. ábra jelöléseit használva:
\(\displaystyle a=2r\sin20^{\circ},\)
\(\displaystyle b=2r\sin40^{\circ},\)
\(\displaystyle c=2r\sin80^{\circ},\)
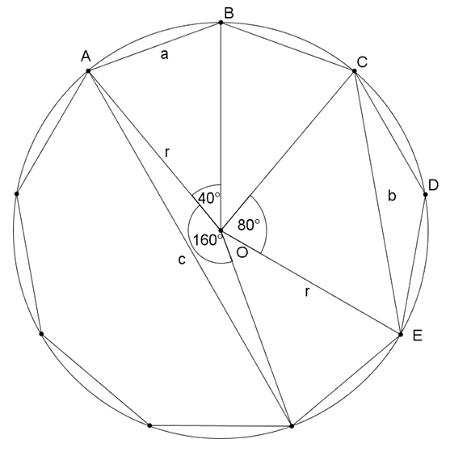
2. ábra
A bizonyítandó állítás: \(\displaystyle c-b=a\).
Az előző értékeket behelyettesítve:
\(\displaystyle 2r\sin80^{\circ}-2r\sin40^{\circ}=2r\sin20^{\circ}.\)
\(\displaystyle 2r\)-rel egyszerűsítve: \(\displaystyle \sin80^{\circ}-\sin40^{\circ}=\sin20^{\circ}\).
\(\displaystyle \sin(60^{\circ}+20^{\circ})-\sin(60^{\circ}-20^{\circ})=\sin20^{\circ},\)
\(\displaystyle \sin60^{\circ}\cos20^{\circ}+\cos60^{\circ}\sin20^{\circ} -\sin60^{\circ}\cos20^{\circ}+\cos60^{\circ}\sin20^{\circ}=\sin20^{\circ},\)
\(\displaystyle 2\cos60^{\circ}\sin20^{\circ}=\sin20^{\circ},\)
\(\displaystyle 2\cdot\frac12\sin20^{\circ}=\sin20^{\circ}.\)
Mivel ezek ekvivalens átalakítások voltak, az állítás igaz.
Statisztika:
101 dolgozat érkezett. 5 pontot kapott: Barta Gergely, Braun Dániel, Bukor Benedek, Cseh Noémi, Dávid Levente, Édes Lili, Fajszi Bulcsú, Fekete Balázs Attila, Ferenczi László, Garamvölgyi István Attila, Geretovszky Anna, Heller-Szabó Anna, Horváth 546 János, Kassai Levente, Marozsák Tóbiás , Molnár 410 István, Molnár Bálint, Nagy Nándor, Négyessy Eszter, Páhoki Tamás, Pinke Andrea, Pszota Máté, Sáfi Lilla, Sal Dávid, Sebe Anna, Sipos Fanni Emma, Szakali Benedek, Szécsi Adél Lilla, Tóth 430 Róbert, Török 111 Emese, Villányi Soma, Weisz Máté, Williams Hajna. 4 pontot kapott: 26 versenyző. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 19 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2016. márciusi matematika feladatai

