 |
A C. 1397. feladat (2017. január) |
C. 1397. Bizonyítsuk be, hogy az
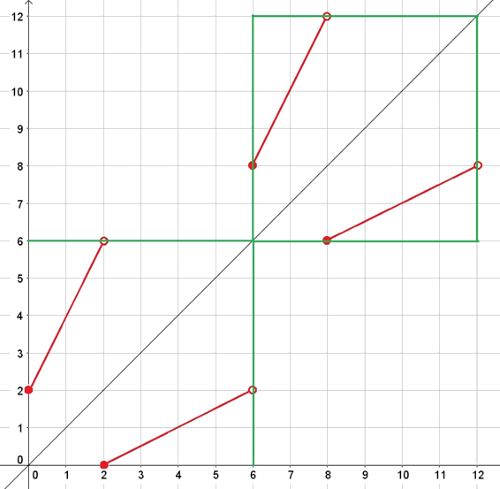
\(\displaystyle f\colon \mathbb{R}\to \mathbb{R},\quad x\mapsto \begin{cases} 2x+2-6k, & \text{ha } x\in \left[6k; 6k+2\right[ ,\\ \frac{x-2+6k}{2}, & \text{ha } x\in \left[6k+2; 6k+6\right[ \end{cases} \quad (k\in \mathbb{Z}) \)
függvény (\(\displaystyle k\) az összes egész értéket felveszi) kölcsönösen egyértelmű, és önmaga inverze.
(5 pont)
A beküldési határidő 2017. február 10-én LEJÁRT.
Megoldás. Az \(\displaystyle y=2x+2\) és az \(\displaystyle y=\frac{x-2}{2}\) függvény szigorúan monoton növekvő. Így az adott függvény minden intervallumon szigorúan monoton növekvő, hiszen a fentiektől csak konstansban különbözik. Az értelmezési tartomány és az értékkészlet intervallumai is diszjunkt halmazok, ezért a hozzárendelés kölcsönösen egyértelmű.
Ha \(\displaystyle x∈[6k;6k+2[\), akkor \(\displaystyle f(x)=y=2x+2-6k\). Behelyettesítéssel láthatjuk, hogy az értékkészlet ehhez az intervallumhoz \(\displaystyle y∈[6k+2;6k+6[\) és \(\displaystyle y=2x+2-6k\).
Ebből \(\displaystyle x\)-et kifejezve: \(\displaystyle x=\frac{y-2+6k}{2}\).
A változókat felcseréve azt kapjuk, hogy ezen az intervallumon a függvény inverze:
\(\displaystyle f^{-1}(x)=\frac{x-2+6k}{2}\), ha \(\displaystyle x∈[6k+2;6k+6[\).
Hasonlóan, ha \(\displaystyle x∈[6k+2;6k+6[\), akkor \(\displaystyle f(x)=y=\frac{x-2+6k}{2}\), behelyettesítéssel az értékkészlet ehhez az intervallumhoz \(\displaystyle y∈[6k;6k+2[\) és \(\displaystyle y=\frac{x-2+6k}{2}\).
Ebből \(\displaystyle x\)-et kifejezve: \(\displaystyle x=2y+2-6k\).
A változókat felcseréve kapjuk a függvény inverzét ezen az intervallumon:
\(\displaystyle f^{-1}(x)=2x+2-6k\), ha \(\displaystyle x∈[6k;6k+2[\).
Ezzel beláttuk, hogy a függvény önmaga inverze.
Statisztika:
36 dolgozat érkezett. 5 pontot kapott: Agócs Katinka, Balbisi Mirjam, Édes Lili, Kocsis Júlia, Kormányos Hanna Rebeka, Kovács 526 Tamás, Mácz Andrea, Nagy Olivér, Németh Csilla Márta, Rittgasszer Ákos, Surján Anett, Szalay Gergő, Szalay Máté Csongor, Szécsi Adél Lilla, Szilágyi Éva, Tatai Mihály, Zsombó István. 4 pontot kapott: Árvai Balázs, Dankowsky Anna Zóra, Gera Dóra, Nagy Odett, Tanács Viktória, Thuróczy Mylan, Wolff Vilmos. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. januári matematika feladatai

