A C. 874. feladat

Rendelje meg a KöMaL-t!

ELTE

VersenyVizsga portál

Kísérletek.hu

Matematika oktatási portál

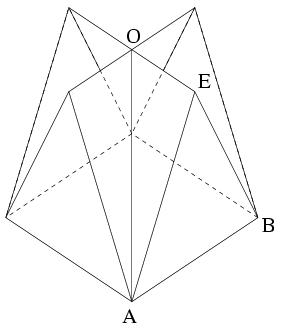
C. 874. Egy 3 m oldalú négyzet alapú újságos pavilon tetőszerkezete két egymást átható szabályos háromoldalú hasáb, amelyek egy-egy oldallapja a mennyezettel esik egybe. (A két hasáb egymáshoz képest 90^o-kal el van forgatva.) Mekkora a tetőfelület nagysága?

(5 pont)

A beküldési határidő LEJÁRT.

Megoldás. A tetőfelület nyolc egybevágó, derékszögű háromszögből tevődik össze. Számítsuk ki egy ilyennek a területét:

$t=t_{{\rm AOE}\triang}=0,5\cdot AE\cdot EO=0,5\cdot3\cdot1,5=0,5\cdot4,5~{\rm m}^2.$

A tetőfelület nagysága tehát 8^.0,5^.4,5 m²=18 m².

Ha a felületbe beleszámítjuk a négy egybevágó, 3 m oldalú szabályos háromszög területét is, akkor nagysága $18+4\cdot0,5\cdot3\cdot\frac{\sqrt3}{2}\cdot3~{\rm m}^2=18+9\sqrt3~{\rm m}^2\approx33,59~{\rm m}^2$ .

A C. 874. feladat statisztikája

353 dolgozat érkezett.

5 pontot kapott: 230 versenyző.

4 pontot kapott: 76 versenyző.

3 pontot kapott: 12 versenyző.

2 pontot kapott: 11 versenyző.

1 pontot kapott: 6 versenyző.

0 pontot kapott: 17 versenyző.

Nem versenyszerű: 1 dolgozat.

A KöMaL 2006. novemberi matematika feladatai

Támogatóink:

ELTE