 |
Az I. 311. feladat (2013. január) |
I. 311. Egy park frissen rendezett téglalap alakú területén járólaprakó géppel teszik le az egységnyi oldalhosszúságú négyzet alakú betonlapokat. A gép egy lépésben előre, hátra, illetve jobbra vagy balra egy egységnyit tud lépni. Minden lépésnél egy betonlapot letesz a földre. A járólapfektetés közben önmagát keresztezheti az út. A gép ebben az esetben egymásra rakja a lapokat. Az így keletkező felesleget később össze kell gyűjteni.
A gép munkájához előre meg kell adni az útvonalát a terület vízszintes és függőleges hosszegységekben mért koordináta-sorozatával egy állományban. Az állomány soronként tartalmazza a gép x és y koordinátáit (3 N
N 100). A gép egy feltöltéssel, egy programmal maximum 200 járólapot tud letenni és a terület bármely pontjából indulhat.
100). A gép egy feltöltéssel, egy programmal maximum 200 járólapot tud letenni és a terület bármely pontjából indulhat.
Táblázatkezelő program segítségével oldjuk meg a következő feladatokat. A megoldásban saját függvény vagy makró nem használható.
1. Töltsük be a tabulátorokkal tagolt, UTF-8 kódolású - honlapunkról letölthető - utterv.txt szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. Munkánkat i311 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. Sorok és oszlopok beszúrásával, majd a cellák feltöltésével hozzuk létre a minta szerinti fejlécet.
3. A járólaprakó gép útvonalát, a területre lerakott betonlapok helyét karakteres formában is megjelenítjük. Ehhez végezzünk el néhány beállítást. A megjelenítéshez használandó oszlopok szélességét és sorok magasságát állítsuk be úgy, hogy a cellák négyzet alakúak legyenek a képernyőn. A sor- és oszlopkoordinátákat félkövér betűstílussal jelenítsük meg.
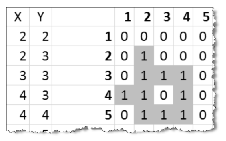
4. Másolható függvény segítségével a terület minden pontjában határozzuk meg, hogy a gép programjának végrehajtása után hány betonlap lesz azon a helyen. Segédszámításokat tetszőleges oszlopban végezhetünk, de ezeket ne rejtsük el.
5. Feltételes formázással emeljük ki a cellamintázat színezésével a gép útvonalát. A munkalapot nevezzük át Terkep nevűre.
6. A munkafüzetben hozzunk létre új munkalapot Elemzes néven. A további kérdésekre ezen a munkalapon válaszoljunk. Segédszámításokat itt is tetszőleges oszlopban végezhetünk, de ezeket se rejtsük el.
7. Számoljuk ki, hogy az egész terület hány százaléka járólap nélküli.
8. Mennyi az egymásra letett betonlapok maximális száma és hol van ez? Több azonos értékű pont esetén elég az egyik koordinátáit megadni.
9. Adjuk meg a terület négy széléhez legközelebbi betonlapok koordinátáit. Azonos távolságú járólapok esetén csak az egyikét.
10. Számoljuk meg, hogy hány darab járólapot kell elvinni ahhoz, hogy egymásra téve egy se maradjon.
11. Ha a felesleges járólapokat csak egyesével tudjuk elvinni a (0;0) koordinátájú, a területen kívül eső pontba, akkor mekkora utat kell összesen megtenni? A szállítás során csak felfelé és balra léphetünk.
Beküldendő a táblázatkezelő munkafüzet (i311.xls, i311.ods, ...), illetve egy rövid dokumentáció (i311.txt, i311.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
Letölthető állomány: utterv.txt
(10 pont)
A beküldési határidő 2013. február 11-én LEJÁRT.
Mintamegoldás:
Qian Lívia 10. évfolyamos tanuló (Szeged, SZTE Ságvári Endre Gyakorló Gimnázium) megoldását közöljük: i311.xlsx
Statisztika:
8 dolgozat érkezett. 10 pontot kapott: Fényes Balázs, Gema Barnabás, Qian Lívia. 9 pontot kapott: Jákli Aida Karolina, Kalló Kristóf, Tomku György. 8 pontot kapott: 1 versenyző. 7 pontot kapott: 1 versenyző.
A KöMaL 2013. januári informatika feladatai

