A KöMaL 2007. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2007. május 11-én LEJÁRT. |
M. 278. Vizsgáljuk meg kísérletileg, hogy mikor áll meg hamarabb az inga, ha nagyobb vagy ha kisebb méretű golyó van a fonál végén! Függ-e a megállási idő a golyó anyagától?
Közli: Varga István, Békéscsaba
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2007. május 11-én LEJÁRT. |
P. 3973. Júliusban a nagy meleg miatt naponta átlagban 3 órán keresztül volt bekapcsolva a légkondicionáló klímaberendezés. Ennek hasznos hűtési teljesítménye 1800 W. 230 V-os hálózatról működik úgy, hogy a hasznos teljesítmény a hálózatból felvett teljesítménynek 240%-a. Mennyivel nőtt a klímaberendezés működése következtében a júliusi villanyszámlánk? Tegyük fel, hogy 1 kWh villamos energia ára 36 Ft.
Közli: Nagy Ágnes, Budapest
(3 pont)
P. 3974.  =20o-os lejtő tetejéről csúszik le egy m1=2 kg tömegű test. Ehhez a testhez van erősítve egy csigán átvetett
=20o-os lejtő tetejéről csúszik le egy m1=2 kg tömegű test. Ehhez a testhez van erősítve egy csigán átvetett  =1,6 m hosszú fonállal a rajz szerinti vízszintes pályán lévő, m2=1 kg tömegű kiskocsi. A fonál kezdetben egyenes. A lejtő első
=1,6 m hosszú fonállal a rajz szerinti vízszintes pályán lévő, m2=1 kg tömegű kiskocsi. A fonál kezdetben egyenes. A lejtő első  /2 hosszúságú szakaszán a súrlódás elhanyagolható, a második
/2 hosszúságú szakaszán a súrlódás elhanyagolható, a második  /2 hosszúságú szakaszán pedig
/2 hosszúságú szakaszán pedig 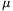 =0,6. Milyen messze lesznek egymástól a testek, amikor a kiskocsi a csigához ér?
=0,6. Milyen messze lesznek egymástól a testek, amikor a kiskocsi a csigához ér?
Közli: Holics László, Budapest
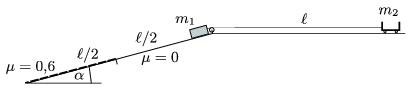
(4 pont)
P. 3975. Egy hosszú és sötét folyosó mindkét végére beépítettek egy-egy kétállású villanykapcsolót. A folyosó közepén lévő lámpa bármelyik kapcsolóval ki-be kapcsolható.
a) Készítsük el a kapcsolási rajzot!
b) Az idő hányad részében ég a lámpa, ha egy automata az egyik kapcsolót két percenként, a másikat három percenként kapcsolja át?
Közli: Bakonyi Gábor, Budapest
(4 pont)
P. 3976. A légpárnás asztalon lévő R sugarú korongot mindvégig állandó u sebességgel mozgatjuk. A korongnak ütközik rugalmasan egy vele párhuzamosan v0=0,3 m/s sebességgel mozgó másik, kisméretű korong. Az ábrán látható d távolság R/2 nagyságú; a korongok közti súrlódás elhanyagolható.
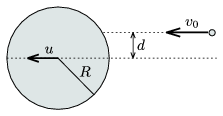
a) Mekkora u esetén fog a kisméretű korong az ütközés után éppen az eredeti mozgásirányára merőlegesen mozogni?
b) Mekkora lesz ilyenkor a kisméretű korong sebessége a rugalmas ütközés után?
Közli: Kotek László, Pécs
(5 pont)
P. 3977. Mennyivel változtatja meg a gravitációs gyorsulás nagyságát a földkéregben lévő gömb alakú olajmező, ha a gömb sugara 10 km, a középpontja pedig 11 km mélyen van a Föld felszíne alatt?
Számítsuk ki, hogy mennyi a változás a Föld felszínén pontosan az olajmező fölött, illetve ettől a ponttól 20 km távolságban!
Közli: Cserti József, Budapest
(5 pont)
P. 3978. Egy m tömegű és  =1 m hosszúságú rúd egyik végével az
=1 m hosszúságú rúd egyik végével az  =60o-os lejtőn, másik végével pedig a vízszintes talajon súrlódásmentesen mozogva lecsúszik. Kezdetben a rúd a lejtőhöz simulva áll, mozgásának egy közbülső helyzetét látjuk az ábrán.
=60o-os lejtőn, másik végével pedig a vízszintes talajon súrlódásmentesen mozogva lecsúszik. Kezdetben a rúd a lejtőhöz simulva áll, mozgásának egy közbülső helyzetét látjuk az ábrán.
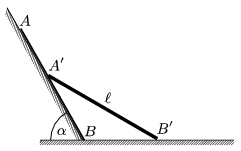
a) Mekkora a rúd A, illetve B végpontjának sebessége, amikor a rúd eléri a vízszintes helyzetet?
b) Mekkorák ezek a sebességek, amikor a rúd 30o-os szöget zár be a vízszintessel?
Közli: Balogh Péter, Váchartyán
(5 pont)
P. 3979. Q és -4Q pontszerű töltéseket rögzítettünk egymástól L távolságra.
a) Hol lesz zérus az eredő térerősség?
b) Hol lesz zérus az eredő potenciál?
(A potenciált - szokásos módon - a végtelenben vegyük nullának!)
Közli: Simon Péter, Pécs
(5 pont)
P. 3980. Egy vezetékpáron 100 kW teljesítményt kell 100 km távolságra eljuttatni úgy, hogy a feszültség csökkenése legfeljebb 2% lehet. A távvezeték anyaga réz, amelynek fajlagos ellenállása 1,7.10-8 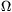 m, a vezeték átmérője 20 mm. Mekkora feszültségre van szükség?
m, a vezeték átmérője 20 mm. Mekkora feszültségre van szükség?
Schwartz-verseny, Nagyvárad (Románia)
(4 pont)
P. 3981. Állandó feszültségű, de változtatható frekvenciájú váltóáramú generátort kapcsolunk egy soros RLC-körre. A frekvenciát fokozatosan növelve az áram elér egy maximumot, ekkor a tekercs feszültsége U1. A frekvencia további növelésekor az áram ugyan csökken, a tekercsen a feszültség azonban tovább nő. Később a tekercs feszültsége is elér egy maximális U2 értéket, majd csökkenni kezd.
Határozzuk meg az hányadost R, L és C függvényében!
Közli: Veres Zoltán, Margitta (Románia)
(5 pont)
P. 3982. Az elemek átalakításához ma már megfelelő nukleáris technológia áll rendelkezésre. Vizsgáljuk meg, hogy milyen lépésekben lehet stabil bizmutból stabil ólmot előállítani!
Közli: Radnai Gyula, Budapest
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

