A KöMaL 2014. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2014. március 10-én LEJÁRT. |
M. 339. Határozzuk meg, hogy a kockacukor térfogatának hány százaléka a cukor térfogata!
Közli: Homoki-Nagy Olga, Monor
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2014. március 10-én LEJÁRT. |
P. 4605. Az ábrán látható kapcsolásban az áramforrások kapocsfeszültsége állandó, U1=15 V és U2=45 V. Az ellenállások értéke R1=10 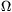 és R2=20
és R2=20 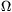 .
.
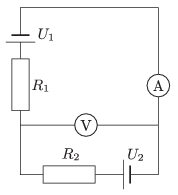
a) Mennyit mutatnak az ideálisnak tekinthető műszerek?
b) Oldjuk meg a feladatot úgy is, ha a két műszert felcseréljük egymással!
Közli: Zsigri Ferenc, Budapest
(3 pont)
P. 4606. Egy tömegpont mozgása két szakaszra bontható. Az első szakaszon az átlagsebessége v1, a másodikon v2. A teljes útra vonatkozó átlagos sebesség v1 és v2 mértani közepe: . Adjuk meg a két útszakasz arányát!
Közli: Simon Péter, Pécs
(4 pont)
P. 4607. A rendőrségi motoros kishajó orra magasan kiemelkedik a vízből, miközben egy adott helyre sietnek vele. Függ-e a kiemelkedés mértéke a kishajó sebességétől? Ábrázoljuk vázlatosan a hajóra ható erőket!
Közli: Radnai Gyula, Budapest
(4 pont)
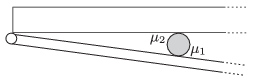
P. 4608. Hogy a huzat ne csapja be az ajtót, egy függőleges tengelyű, lapos henger alakú tárgyat helyezünk az ajtó és a küszöb közé, lehetőleg közel az ajtó forgástengelyéhez. Mekkora szögig képes a huzat behajtani az ajtót, ha a csúszó súrlódási együttható az ajtó és a tárgy között 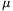 1, a küszöb és a tárgy között
1, a küszöb és a tárgy között 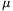 2?
2?
Közli: Bártfai Pál, Budapest
(5 pont)
P. 4609. Egy vízszintes, vékony cső mindkét vége zárt. A cső közepén egy h hosszúságú higanyszál van. A levegőoszlopok hossza mindkét térrészben  , a nyomás mindkét oldalon H magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. A csövet egy függőleges tengelyű centrifugagépre helyezzük, és forgásba hozzuk.
, a nyomás mindkét oldalon H magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. A csövet egy függőleges tengelyű centrifugagépre helyezzük, és forgásba hozzuk.
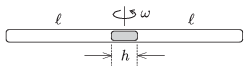
Adjuk meg a higanyszál elmozdulását az 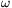 szögsebesség függvényében, ha a hőmérséklet állandó!
szögsebesség függvényében, ha a hőmérséklet állandó!
Varga István (1952-2007) feladata
(5 pont)
P. 4610. Súrlódásmentesen mozgó dugattyúval elzárt, vízszintes szimmetriatengelyű, hengeres tartályban ideális gáz van. Kezdetben a gáz térfogata V1, hőmérséklete T1, a nyomása p1, ami megegyezik a külső (és a későbbiekben is állandó) légnyomással.
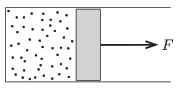
A tartályban lévő gázon többször egymás után a következő műveleteket végezzük: Állandó nyomáson felmelegítjük T2 hőmérsékletre, majd pedig az elért térfogatát állandónak tartva, visszahűtjük T1-re. Ezt egymás után n-szer tesszük meg. Az egyes lépésekben az állandó nyomáson történő melegítéskor a dugattyúra külső, lépésenként más-más értékű, de állandó erőt is kell alkalmaznunk. A teljes folyamat során összesen W munkát végzünk.
a) Mekkorára nő a gáz térfogata n lépés után?
b) Mennyi a külső erő által elvégzett W munka összesen?
Közli: Légrádi Imre, Sopron
(5 pont)
P. 4611. Igen nagy alapterületű, földelt fém padlójú helyiségben a h magasságú mennyezethez egy 0,7 h nyugalmi hosszúságú, D direkciós állandójú, szigetelő gumiszál egyik végét rögzítjük, másik végére egy könnyű, kicsi fémgömböt kötünk. Ha a gömböt Q töltéssel feltöltjük, akkor a gumiszál hosszúra nyúlik. Sikerülhet-e igen lassan a gömb töltését 3Q-ra növelni anélkül, hogy az hozzáérne a padlóhoz? (A mennyezet és a falak elektrosztatikus hatását elhanyagoljuk.)
Közli: Bilicz Sándor, Budapest
(5 pont)
P. 4612. Egy 30 cm-re lévő tárgyat nézünk egy lencsén keresztül. Amikor a lencse közel van akár a szemünkhöz, akár a tárgyhoz, akkor eredeti nagyságában látjuk a tárgyat, a két helyzet között azonban nagyobbnak látjuk.
a) Hol van a lencse, amikor legnagyobbnak látjuk a tárgyat?
b) Mekkora a fókusztávolság, ha az a) esetben a tárgyat az eredeti nagyságánál kétszer nagyobbnak látjuk?
Közli: Tichy Géza, Budapest
(5 pont)
P. 4613. Egy stabilizált feszültségű tápegységre 1 méter hosszú, szigeteletlen, homogén, mindenütt azonos keresztmetszetű huzalellenállást kapcsolunk. Egy, a huzallal azonos ellenállású fogyasztó egyik kivezetését a huzalellenállás végéhez kapcsoljuk, másik kivezetését csúsztatjuk a huzalon.
Hol van a csúszóérintkező, amikor a fogyasztó teljesítménye éppen negyedrésze az ebben a kapcsolásban elérhető legnagyobb teljesítményének?
Közli: Szombathy Miklós, Eger
(4 pont)
P. 4614. Függőleges, igen hosszú, egyenes szigetelőszál vonalmenti töltéssűrűsége 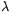 =8.10-7 C/m. A száltól d0=5 cm távolságban igen vékony,
=8.10-7 C/m. A száltól d0=5 cm távolságban igen vékony,  =10 cm hosszú szigetelő fonálra felfüggesztettünk egy m=2 g tömegű, q=6,81.10-8 C töltésű, igen kis méretű fémgolyót. A fonál függőleges állapotában a fémgolyót szigetelő eszközzel rögzítjük. Egy adott pillanatban a rögzítést lökésmentesen megszüntetjük. Határozzuk meg, hogy
=10 cm hosszú szigetelő fonálra felfüggesztettünk egy m=2 g tömegű, q=6,81.10-8 C töltésű, igen kis méretű fémgolyót. A fonál függőleges állapotában a fémgolyót szigetelő eszközzel rögzítjük. Egy adott pillanatban a rögzítést lökésmentesen megszüntetjük. Határozzuk meg, hogy
a) Maximálisan milyen messze távolodik el a fémgolyó a függőleges fémszáltól?
b) Mekkora szöget zár be a fonál a függőlegessel, amikor a golyó sebessége maximális?
Közli: Holics László, Budapest
(5 pont)
P. 4615. A lépcsőjáró vagy más néven ,,slinky'' egy olyan rugó, amelynek nyújtatlan hossza elhanyagolhatóan kicsi, jó közelítéssel követi a Hooke-törvényt, és már a saját súlya hatására is számottevően megnyúlik.

a) Az asztalon nyugvó, m tömegű slinky-t a felső végénél fogva lassan addig emeljük, amíg az alsó vége éppen elválik az asztaltól. Ekkor a rugó hossza L. Mekkora munkát végeztünk az emelés közben?
b) Ha ebben a helyzetben elengedjük a rugót, a legalsó menet érdekes módon egészen a teljes összecsukódásig nem mozdul meg (lásd az ábrát). Mekkora sebességgel kezd esni a slinky közvetlenül a teljes összecsukódás után?
Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

